几道2017年国外数学奥林匹克不等式题的优雅证明

彭小奇

江西省萍乡市湘东中学 (337016)

本文旨在给出几道最新的国外数学奥林匹克不等式题的优雅证明，里面渗透了命题人和答题者的许多心思和智慧，供读者学习和玩味.

注1：此题平而不俗，此证非常大气.

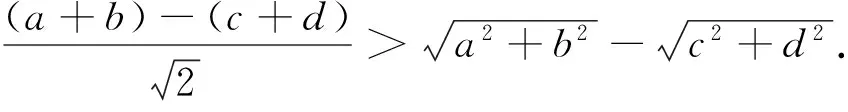
注3：证明1是分析法开道，综合法书写.证明2充分体现了答题者代数变形的功力.

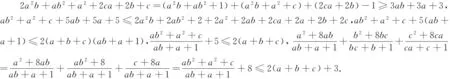
注4：不等式研究弘扬的是不断尝试、坚定探索的科学精神.

注5:此证看似简单，但含金量很高，值得细细品味.

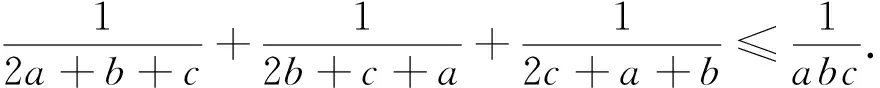
注6:不等式证明方法中蕴含着丰富的辩证法思想.

例7 (2017年以色列数学奥林匹克)已知a,b,c是满足a2+3b2+7c2=11的非负实数，求证：2b+6c+abc≤9.

证明：因为a2-1,b2-1,c2-1中必有两个不同时大于零或者不同时小于零，故不妨设(a2-1)(b2-1)≤0，于是a2+b2≥a2b2+1，a2+b2+c2-2abc≥a2b2+c2-2abc+1≥1，1≤a2+b2+c2-2abc=a2+3b2+7c2-2(b2+3c2+abc),1≤11-2(b2+3c2+abc)，∴b2+3c2+abc≤5，2b+6c+abc≤b2+1+3(c2+1)+abc≤9.