一类非线性发展方程的整体吸引子
2018-03-23孙晶晶张建文
孙晶晶,张建文
(太原理工大学 数学学院,太原 030024)
非线性发展方程整体吸引子的存在性是动力系统中广泛研究的问题之一,比如非线性发展方程
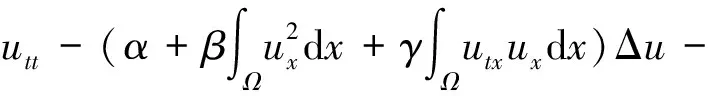
(1)
式中:α,β,γ,μ为正常数;f(u)∈C0(R,R),Ω⊂Rn,且具有足够光滑的边界。当α=1,β=0,γ=0时,关于系统(1)的适定性问题和长时间行为已有了很好的结果,如尚亚东[1]研究了其整体强解的存在性和唯一性;张宏伟等[2]利用势井方法研究了整体弱解的存在性,渐近性和不存在性;XIE et al[3]应用一种新的方法研究了该问题的长时间行为以及当μ=1时的渐近行为;牛丽芳等[4]研究了系统具有记忆项时整体吸引子的存在性。文献[5]在前人的基础上研究了当μ=1时,α,β,γ均为正常数系统的初边值问题。
XIE et al[6]应用文献[7-9]中介绍的方法在R3中研究了一类半线性发展方程的渐近光滑性和整体吸引子
(|ut|r-2ut)t-Δu-Δut-Δutt+f(u)=g,x∈Ω,u|t=0=u0,ut|t=0=u1,x∈Ω,u|∂Ω=0 .
(2)
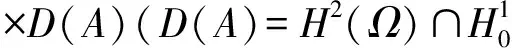
综合考虑式(1)和式(2),可建立如下更为一般的非线性发展方程

(3)
u|t=0=u0,ut|t=0=u1,x∈Ω.
(4)
u|∂Ω=0 .
(5)
式中:非线性函数M(·),N(·)是由于材料的非线性本构关系所致的,有界开集Ω⊂R3,并且具有光滑的边界∂Ω;常数α,μ>0,3≤r≤6;u(x,t)为未知函数;f(u)∈C1(R,R)为给定的满足适当条件的非线性项;g(x)∈L2(Ω)为给定泛函。相比较文献[6-7],本文讨论的方程更具有一般性,并从后面的讨论会发现,增加非线性函数M(·)和N(·)之后带来了很多困难。以下内容分为两部分:一是介绍了系统的先验估计;二是先用Galerkin方法验证了解的存在唯一性,然后应用条件(C)[13]的方法证明了系统存在整体吸引子。
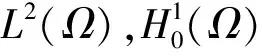
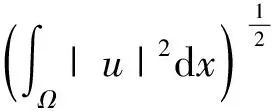
而且若设X,Y为巴拿赫空间,‖·‖X,‖·‖Y分别为空间X与Y的范数,则对∀(u,v)T∈X×Y,定义其范数为
‖(u,v)T‖X×Y=‖u‖X+‖u‖Y.
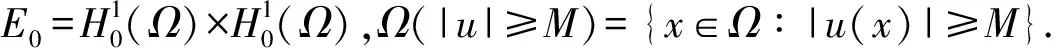
本文中非线性项f(s)∈C1(R,R)满足如下的假设:
|f(r)-f(s)|≤C(1+|r|4+|s|4)|r-s|,r,s∈R.
(6)
而且,令f满足分解f=f0+f1,其中f0,f1∈C1(R,R)也满足
|f0(s)|≤C(1+|s|5),∀s∈R.
(7)
f0(s)s≥0,∀s∈R.
(8)
|f1(s)|≤C(1+|s|p),p<5,∀s∈R.
(9)
(10)
式中:λ1为-Δ在狄利克雷边界条件下的第一特征值,则由式(6)与式(8)可知存在常数C>0,λ<λ1,使得
f(s)s≥f1(s)s≥-λs2-C,∀s∈R.
(11)
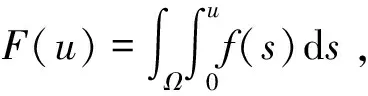
(12)
(13)
1 系统(3)-(5)的先验估计
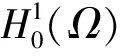
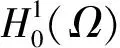

(14)
以及初始条件
(15)

(16)
分别取φ=ωj;j=1,2,…,m,则式(14)-(16)是一个非线性常微分方程组的柯西问题。由常微分方程理论可知:存在tm>0,使得在[0,tm]上存在唯一的解um(t)(0≤t 下面将得到关于解um(t)的先验估计: M(0)=0,N(0)=0,sN(s)≥0,M(s)≥a+bs(b>0) . (17) 则对任意的T>0方程(3)-(5)的解u满足: (18) ((|umt|r-2umt)t-[α+M(zm(t))+N(zmt(t))]Δum-μΔumt-Δumtt+f(u),umt)=(g(x),umt) . 其中 也就有 (18) 在[0,t](t (19) 根据式(17)可得: (20) 又由f的连续性有F(um(x,0))→F(u0m).因此, 从而不等式(20)左端的各项对于一切自然数m及任意t∈[0,T]均有界,故存在正常数M1(R)使得式(17)成立。 (21) 证明:在式(14)中取φ=umtt可得 (22) 由Young不等式及Hölder不等式可知 而且应用中值定理可得 由式(7)与式(9),综合Sobolev嵌入定理以及Poincare'不等式 故式(22)可以简化为: (23) (24) dx)]Δu-μΔut-Δutt+f(u)-g(x),φ)=0 . (25) u|t=0=u0(x),ut|t=0=u1(x) . (26) 证明:由引理1和引理2,应用Galerkin方法可以很容易的得到解的存在性。下面我们来证明该问题的弱解是唯一的,且连续依赖于初值。 假设u,v分别是系统(3)-(5)对应于初值(u0,u1),(v0,v1)的两个解,令ω=u-v,则ω满足以下初边值问题 (27) ω|t=0=ω0,ωt|t=0=ω1,x∈Ω. (28) ω|∂Ω=0,t>0 . (29) 用ωt分别与式(27)两端作L2(Ω)中的内积可得: (r-1)(utt(|ut|r-2-|vt|r-2)+|vt|r-2ωtt,ωt). (29) 其中, 而且, 所以, (30) 注意到M(a)2-M(b2)≤M'(sup{a2,b2})|a-b||a+b|,故 又由中值定理以及M',N'的连续性可知: 同理 故 (31) 最后来处理非线性项,由假设式(6) (32) 综合式(30)-(32),式(29)可以简化为 所以, (33) 下面用ωtt与式(27)两端作L2(Ω)的内积: (33) 其中, (34) (35) (36) (37) 综合式(34)-(37)可得 (38) 从而由式(33),式(38)可知: (39) 式中:K为正常数。对式(39)应用Gronwall引理可得: (40) 显然,若u0=υ0,u1=υ1,则ω=ωt=0,从而解的唯一性得证。 (41) 由定理1和引理3可以定义半群 而且满足通常的半群性质: S(t+s)=S(t)S(s),S(0)=I,∀t,s≥0 . (42) 且不难证明,对一切t≥0,{S(t)}都是连续的。 定义1[14]空间X上的半群{S(t)}t>0满足条件(C):如果对任意的ε>0和X中的任何有界集B,存在tB≥0和X的有限维子空间X1,使得对任意的t≥tB都有{PS(t)x|x∈B,t>tB}是有界的,而且对任意的x∈B,均有‖(I-P)S(t)x‖X≤ε,其中P∶X→X1是有界投影,I是恒等映射。 引理4[14]假设Z是Banach空间,{S(t)}t≥0是在Z上的C0半群,如果{S(t)}t≥0满足如下条件: 1) {S(t)}t≥0在Z中具有有界吸收集B0; 2) {S(t)}t≥0在Z中满足条件(C),则称{S(t)}t≥0在Z中存在整体吸引子。 下面证明半群{S(t)B}t≥0的耗散性。 定理2 动力系统(3)在E0上具有有界吸收集;也就是对任意有界集B0⊂E0,存在T0=T0(B)使得 S(t)B⊂B0,∀t≥T0. (43) 证明:设v=ut+δu,并将方程式(3)-(5)的第1个式子化为如下形式 (44) 用v与式(44)作内积,并且假设δ足够小则有 (45) (46) 为方便,简单记为 以及 从而方程式(46)可以简化为 也就有 (47) 其中 (48) 根据式(11)和式(12),并应用Young不等式可得 (49) (50) 其中 则有 结合式(48)应用引理2可知 所以 (51) 所以对任意的t≥T0(B),都存在Q>0使得 (52) 定理3 动力系统(3)的解半群{S(t)}t≥0在E0中存在整体吸引子A,即A在E0中是紧的,不变的,且按E0中的范数吸引E0中任意有界集。 证明:应用引理4,现在只需证明解半群{S(t)}t≥0在空间E0中满足条件(C)即可。 0≤λ1≤λ2≤λ3≤…,λi→∞,当i→∞ . 若设Hm=span{ω1,ω2,…,ωm},对于∀(u,ut)T∈E0则有如下唯一的分解 (u,ut)T=(u1,u1t)T+(u2,u2t)T. 应用式(44)与v2作L2(Ω)中的内积,可得 (53) 由Sobolev嵌入定理以及定理2可知,对任意的ε>0,存在T=T(B,ε)和m(空间Hm的维数),使得对一切t≥T,n≥m都有以下估计成立: 综合以上估计: (54) 结合引理4和定理2可知:系统(3)的半群{S(t)}在E0中有整体吸引子A. [1] 尚亚东.方程utt-Δu-Δuτ-Δutt=f(u)的初边值问题[J].应用数学学报,2000,23(3):385-393. SHANG Y D.Initial boundary value problem of equationutt-Δu-Δuτ-Δutt=f(u)[J].Acta Mathematicae Applicatae Sinica,2000,23(3):385-393. [2] 张宏伟,呼青英.一类非线性双曲方程整体弱解的存在性和不存在性[J].工程数学学报,2003,20(3):131-134. ZHANG H W,HU Q Y.Existence and nonexistence of solution for a class nonlinear hyperbolic equation[J].Journal of Engineering Mathematics,2003,20(3):131-134. [3] XIE Y Q,ZHONG C K.The existence of global attractors for a class nonlinear evolution equation[J].Journal of Mathematical Analysis and Applications,2007,336(1):54-69. [4] 牛丽芳,张建文,张建国.一类带记忆项的非线性弹性杆的全局吸引子[J].数学的实践与认知,2013,43(18):262-268. NIU L F,ZHANG J W,ZHANG J G.Existence of global attractors for a class of nonlinear elastic rod equation with memory type[J].Mathematics in Practice and Theory,2013,43(18):262-268. [5] 牛丽芳,张建文.一类具有黏阻尼的非线性弹性杆方程的初边值问题[J].太原理工大学学报,2014,45(1):128-132. NIU L F,ZHANG J W.Initial-boundary value problems for a kind of nonlinear elastic rods with some sui [6] XIE Y Q,HE Z F,XI C,et al.Asymptotic smoothing and global attractors for a class of nonlinear evolution equations[J].ISRN Mathematical Analysis,2015,2013(4):13-19. [7] YANG M,SUN C.Dynamics of strongly damped wave equations in locally uniform spaces:attractors and asymptotic regularity[J].Transactions of the American Mathematical Society,2009,361(2):1069-1101. [8] SUN C,YANG M.Dynamics of the nonclassical diffusion equations[J].Asymptotical Analysis,2008,59(1/2):51-81. [9] ZELIKS.Asymptotic regularity of solutions of a nonautonomous damped wave equationwith a critical growth exponent[J].Communications on Pure & Applied Analysis,2004,3(4):921-934. [10] 张宏伟,呼青英.一类非线性发展方程整体弱解的存在性和稳定性[J].数学物理方程,2004,24(3):329-336. ZHANG H W,HU Q Y.Existence of global weak solution and stability of a class nonlinear evolution equation[J].Acta Mathematica Scientia,2004,24(3):329-336. [11] 杨莉,谢永钦.一类非线性发展方程整体弱解的存在性[J].湖南工业大学学报,2010,24(1) :36-39. YANG L,XIE Y Q.Existence of global weak solution for a class of nonlinear evolution equation[J].Journal of Hunan University of Technology,2010,24(1):36-39. [12] 秦桂香,李妍汝,李青松,等.一类非线性发展方程的全局吸引子[J].湘潭大学自然科学学报,2013,35(1):25-28. QIN G X,LI Y R,LI Q S,et al.Global attractors for a class of nonlinear evolution equations[J].Natural Science Journal of Xiangtan University,2013,35(1):25-28. [13] XIE Y Q,ZHONG C K.Asymptotic behavior of a class of nonlinear evolution equation[J].Nonlinear Analysis,2009,71(11):5095-5105. [14] ZHONG C K,YANG M H,SUN C Y.The existence of global attractors for the norm-to-weak continuous semigroup[J].J Differential Equations,2006,223:367-399.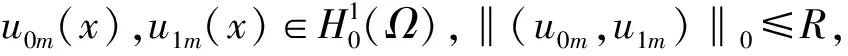
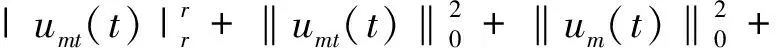
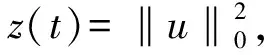



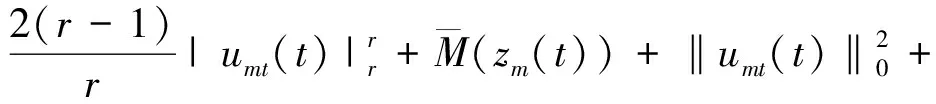
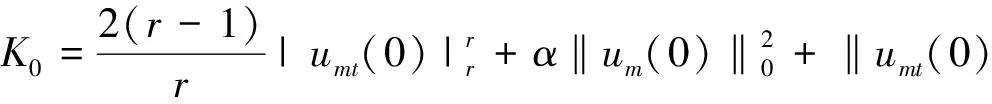
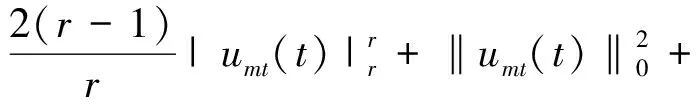
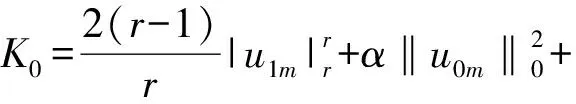
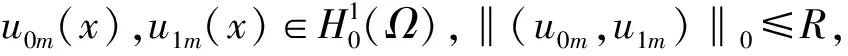
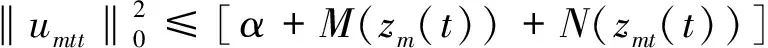
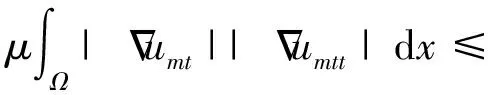
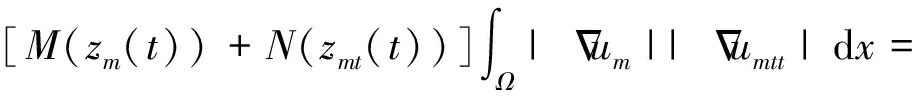
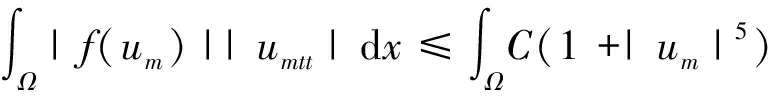
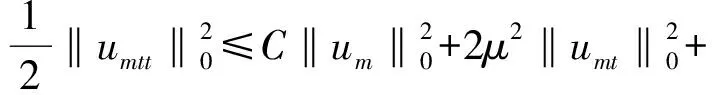
2 整体吸引子
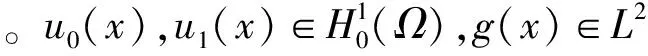
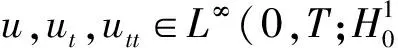
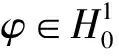

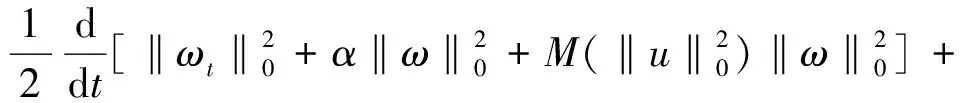


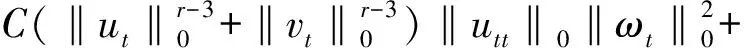
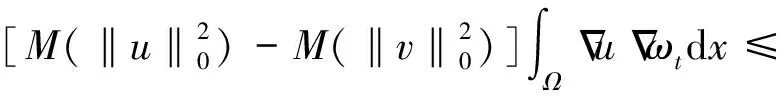
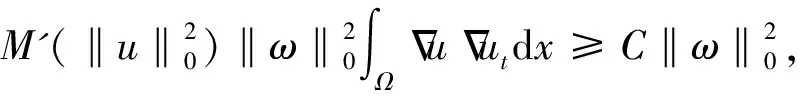



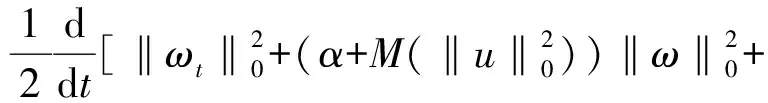

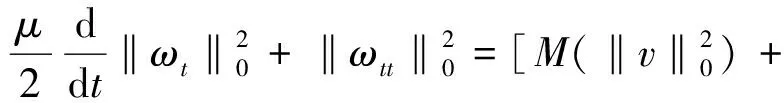

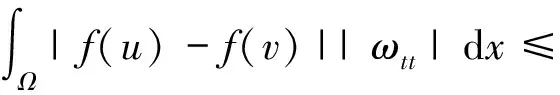
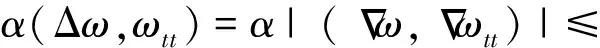
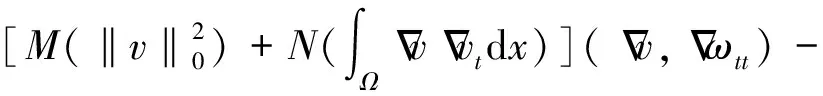
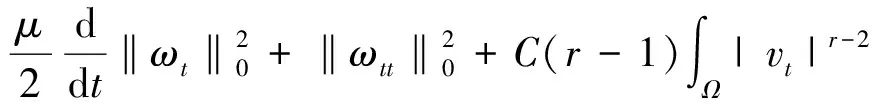
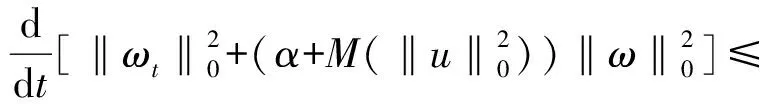

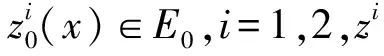
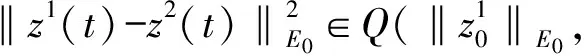





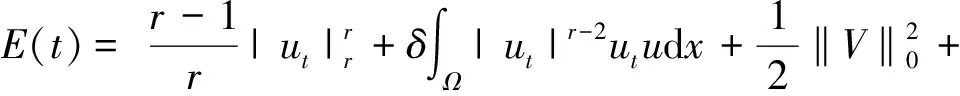


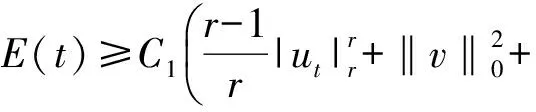
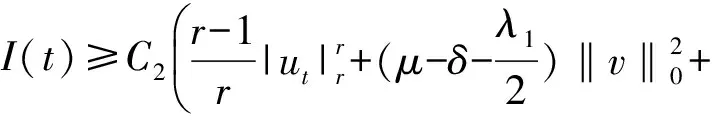
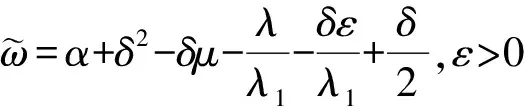
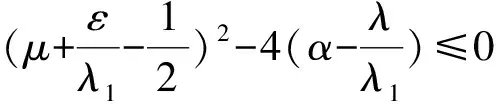
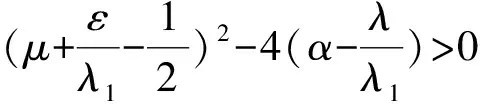
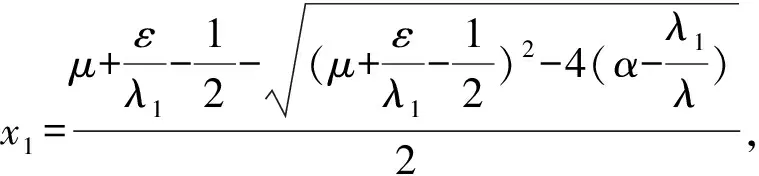
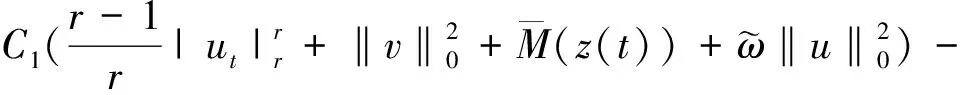
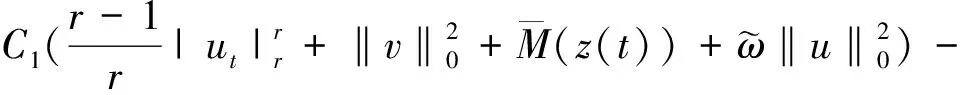
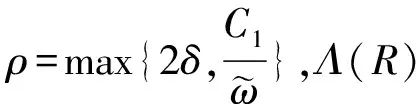
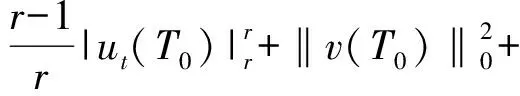
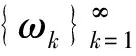
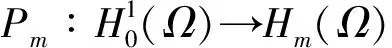
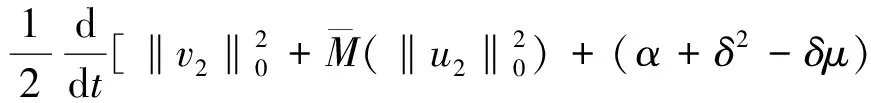
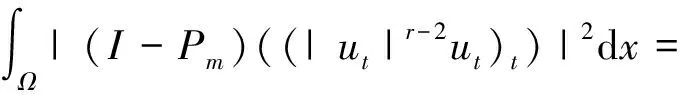
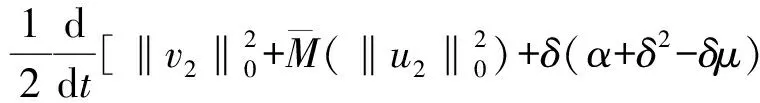
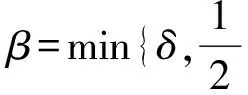
Table damped[J].Journal of Taiyuan University of Technology,2014,45(1):128-132.
