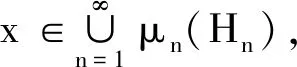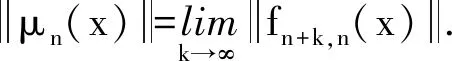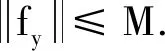Hilbert空间的张量积的连续性
2019-05-22邢美丽
邢美丽
(中国海洋大学 数学科学学院, 山东 青岛 266071)
归纳极限在研究空间性质方面有广泛的作用. 2000年, 纪培胜[1]中探讨了算子空间的定向极限和逆极限并定义了算子空间的Haagerup张量积, 然后证明了Hilbert列空间的无限Haagerup张量积与Hilbert空间的无限张量积是相容的. 2002年, Ryan[2]介绍了巴拿赫空间的张量积并给出了不同的范数. 2018年, Janson Antony[3]研究了算子空间的归纳极限与算子空间的张量积. 在已有文献的基础上, 我们研究了内积空间的归纳极限的概念及其关于张量积的连续性, 这些探索有助于理解C*-代数的逼近与扰动理论.
1 预备知识
定义1[4]若H,K,H′,K′为向量线性空间. 如果μ:H→H′,ν:K→K′, 则存在唯一的映射μ⊗ν:H⊗K→H′⊗K′, 使得对任取x∈H,y∈K均有
(μ⊗ν)(x⊗y)=μ(x)⊗ν(y).
定义2[4]设H,K为Hilbert空间, 则在H与K的代数张量积HΘK上可定义内积:

其中xi,xj∈H,yi,yj∈K, 则HΘK构成内积空间, 完备化记为H⊗K.
2 内积空间的归纳极限的定义

1)对任意的n∈N, 有gn,n=1Hn;
2)对于任意的n≤m≤k, 有gkm∘gmn=gkn;
则称{Hn,gmn}为内积空间的一个正向系.
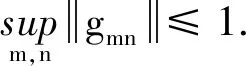
1)对于任意的n≤m, 有φn=φm∘gmn, 即图1可交换;


图1 可交换,φn=φm∘gmn

图2 可交换,ψn=g∘φn
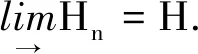
定理1 若内积空间的正向系{Hn,gmn}的归纳极限存在, 则归纳极限在酉等价意义下唯一.
证明: 设(H,φn)和(K,μn)均为正向系{Hn,gmn}的归纳极限, 则对任意的n≤m有:φn=φm∘gmn,μn=μm∘gmn.
由归纳极限的定义, 存在范数小于等于1的有界线性算子g:H→K. 同理, 存在范数小于等于1的有界线性算子f:K→H, 再由唯一性可以得到f∘g=1H, 类似的可以得到g∘f=1K, 这就证明了g为满射. 任取x∈H, 有
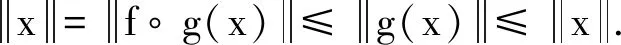
即g为等距的满射. 因此, 归纳极限在酉等价意义下唯一.
以下给出归纳极限的具体构造:
设{Hn}为一列内积空间. 令


设{Hn,gmn}为内积空间的一个正向系. 令
任取{xn}∈H0, 存在正整数N, 当k>N时,


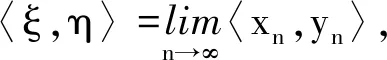

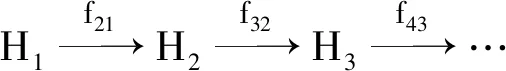

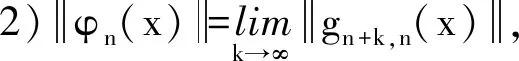

证明1)任给m≥n及x∈Hn, 则有:
φn(x)-φm∘gmn(x)=π(νn(x)-(νm∘gmn)(x))=0.
因此φn=φm∘gmn. 因为∀x∈Hn, 都有φn(x)=φn+1∘gn+1,n(x), 所以有

vN+1(xN+1)=(0,…,0,xN+1,gN+2,N+1(xN+1),…).
2) 由
得

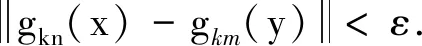
令ε→0, 我们可以得到ψn(x)=ψm(y). 这样我们就可以定义一个映射:
由上可知g的定义合理. 下证g为有界线性算子,
先证g为线性的: 任取α,β∈C,
g(αφn(x)+βφn(y))=ψn(αx+βy)=αψn(x)+βψn(y)=αg(φn(x))+βg(φn(y)).
再证g为有界的: 任取k为整数, 则有
因此,

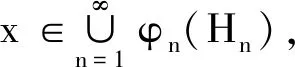
3 Hilbert空间的张量积关于归纳极限的连续性
命题1 若{Hn,fmn}和{Kn,gmn}分别为Hilbert空间的正向系, 则{Hn⊗Kn,fmn⊗gmn}为Hilbert空间的正向系.
证明1)fnn⊗gnn=1Hn⊗Kn;
2)对任意的n (fkm⊗gkm)(fmn⊗gmn)=(fkmfmn)⊗(gkmgmn)=fkn⊗gkn; 因此{Hn⊗Kn,fmn⊗gmn}为正向系. 定义5 设(H,μn)为正向系{Hn,fmn}的任一归纳极限, (K,νn)为正向系{Kn,gmn}的任一归纳极限, 若(H⊗K,φn)为正向系{Hn⊗Kn,fmn⊗gmn}的归纳极限, 则称Hilbert空间的张量积关于归纳极限是连续性的. 定理3 设(H,μn)为正向系{Hn,fmn}的任一归纳极限, (K,νn)为正向系{Kn,gmn}的任一归纳极限, 则(H⊗K,φn)为正向系{Hn⊗Kn,fmn⊗gmn}的归纳极限. 证明设(H,μn)为正向系{Hn,fmn}的归纳极限, (K,νn)为正向系{Kn,gmn}的归纳极限,则可以定义有界线性映射: φn:Hn⊗Kn→H⊗K; 其中k≥i,j,xk=fki(xi),yk=gkj(yj). 下证h定义合理: 设k1>k2≥i,j, 则 ψk2(xk2⊗yk2)=ψk1(fk1k2⊗gk1k2)(xk2⊗yk2)=ψk1(xk1⊗yk1). 则像的取值与k无关. 要证 令 φn+k(xn+k)=ψn+k(xn+k⊗yn+k),n≥0, 其中xn+k=fn+k,k(xk),yn+k=gn+k,k(yk). 显然,φn+k:Hn+k→L是有界线性算子, 且对任意的n≤m有 φm+kfm+k,n+k(xn+k)=ψm+k(xm+k⊗ym+k)=ψm+k(fm+k,n+k⊗gm+k,n+k)(xn+k⊗yn+k)=ψn+k(xn+k⊗yn+k)= 由归纳极限的定义, 存在唯一的有界线性算子fνj(yj):H→L使得φn+k=fνj(yj)∘μn+k. 因此, 固定xi,x=μi(xi), 设(x,νj1(yj1))=(x,νj2(yj2)), 其中i1≥i2, 设k≥i,j1,j2, fy1(x)+fy2(x)=h(x,y1)+h(x,y2)=h(x,y1+y2)=fy1+y2(x). 则任取x∈H, 由fy1,fy2,fy1+y2的连续性知, fy1(x)+fy2(x)=fy1+y2(x). h(x,y1)=fy1(x)→fy2(x)=h(x,y2), 这样h关于x,y分别连续.令gx(y)=h(x,y),fy(x)=h(x,y), 则任取x∈H, 存在Cx, 使得gx(y)≤Cxy, 固定x, 任取y≤1,

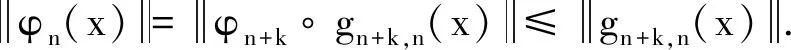






φn+k(xn+k).