对数Bloch空间上某些算子有界的充要条件
2021-05-20刘慧琴
刘慧琴
(闽南理工学院信息管理学院,福建 石狮 362700)
1 预备知识
定义1设D={z:|z|<1}表示复平面上的单位圆盘。
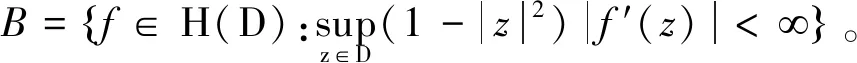
定义3定义LB是对数Bloch空间。如果
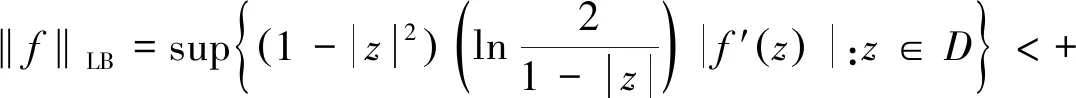
则f∈LB。
‖f‖LB是一个半范数(‖f‖L=|f(0)|+‖f‖LB),所以LB是一个Banach空间。
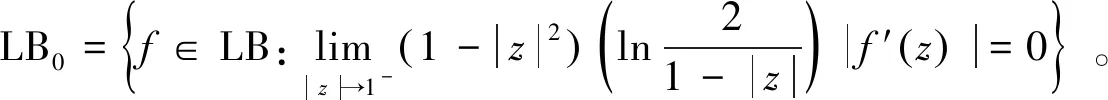
定义4设φ是D上的解析自映射,即φ∈S(D),那么将H(D)上的复合算子定义为Cφ(f)=f(φ(z)),f∈H(D),z∈D。显然Cφ是线性算子。
定义5令g∈H(D),对每个H(D)中的函数f,将Volterra型算子Jg,Ig分别定义为
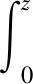
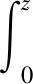
定义6定义Volterra型算子和复合算子的积如下:

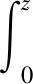

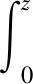
在文献[2]中作者讨论了从单位圆盘上H∞空间和Bloch空间到单位圆盘上的Zygmund型空间上的Volterra 型算子与复合算子的积的有界性和紧性。根据其研究思路和方法,思考如果换到其他空间上来研究Volterra 型算子与复合算子以及这两种算子的积,能否得到这些算子有界性的条件呢?充分必要条件是否都能够得出呢?在文献[3]中已定义了新的空间:对数Bloch空间LB和小对数Bloch空间LB0,然后得到了在LB和LB0上Volterra型算子和复合算子的积的有界性之间的关系。在此基础上本文将首先研究Volterra型算子和复合算子的积分别在对数Bloch空间上和小对数Bloch空间上有界性的充要条件,然后进一步推导出在对数Bloch空间上和小对数Bloch空间上Volterra型算子和复合算子各自的有界性的充要条件。
2 主要结论
引理1[4]假定f∈LB,则
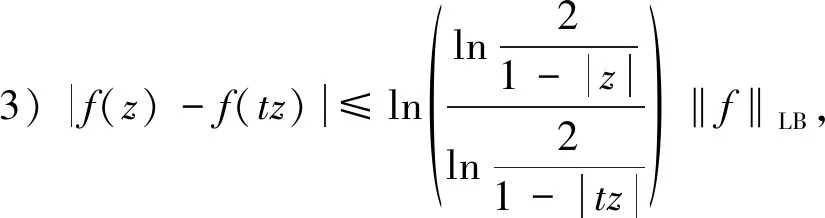
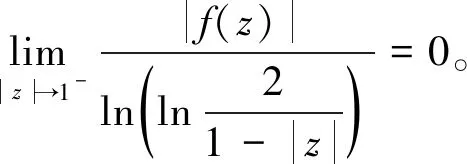
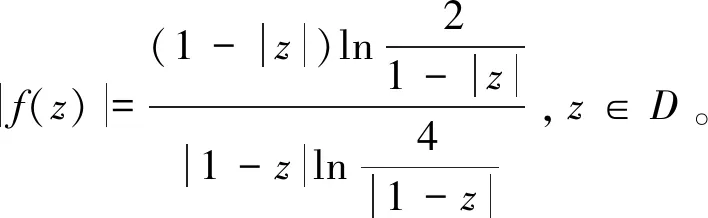
引理4令g∈H(D),φ是D上的解析自映射。如果CφJg(或JgCφ,CφIg,IgCφ)是LB0上的一个有界算子,则CφJg(或JgCφ,CφIg,IgCφ)是LB上的有界算子。
证明此引理已在文献[3]中的定理2给出证明。
这里,先研究算子CφJg(或JgCφ):LB(或LB0)→LB(或LB0)的有界性。
定理1令g∈H(D),φ是D上的解析自映射。则以下结论成立:
1)CφJg:LB→LB是有界的当且仅当
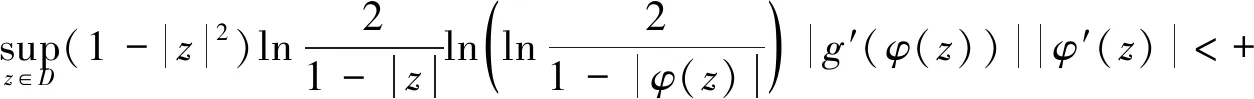
(1)
2)CφJg:LB0→LB0是有界的当且仅当
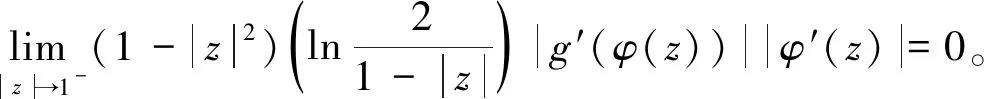
(2)
证明1)假定CφJg:LB→LB是有界的。固定ω∈D,令

(3)
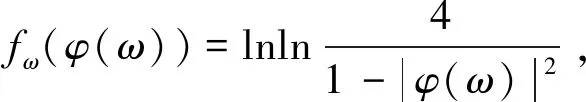
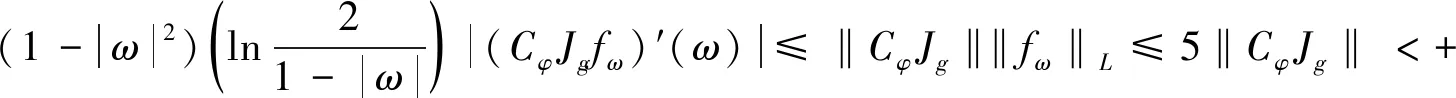
因此式(1)成立。
反过来,假定式(1)成立。则由引理1,有

这表明CφJg有界。
2)假定CφJg:LB0→LB0是有界的。则由引理4知CφJg:LB→LB是有界的。所以由1)知式(1)成立。取f=1,易得式(2)成立。
另一方面,对任意f∈LB0。如果|φ(z)|→1-,当|z|→1-。则由引理2和式(1),有
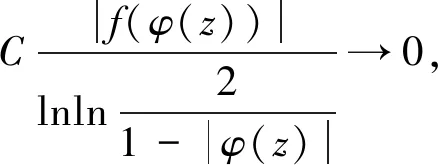
如果|φ(z)|≤r0<1,对每个z∈D。则由式(2)得
|φ′(z)|→0,当|z|→1-时。
所以,对所有f∈LB0,有CφJgf∈LB0。又由1)得CφJg在LB上有界,所以CφJg在LB0上是一个有界算子。
用定理1相同的方法可证得以下结论:
定理2令g∈H(D),φ是D上的解析自映射。则以下结论成立:
1)JgCφ:LB→LB是有界的当且仅当

(4)
2)JgCφ:LB0→LB0是有界的当且仅当式(4)成立且g∈LB0。
从定理1和定理2以及令φ(z)=z,可以得到Jg:LB(或LB0)→LB(或LB0)的有界性。
推论1令g∈H(D),则Jg:LB→LB是有界算子当且仅当Jg:LB0→LB0是有界算子当且仅当
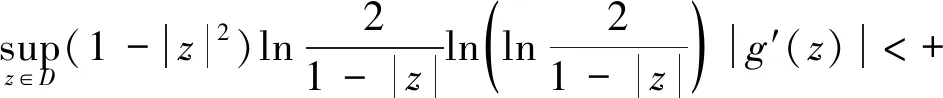
接下来,研究算子CφIg(或IgCφ):LB(或LB0)→LB(或LB0)的有界性。
定理3令g∈H(D),φ是D上的解析自映射,则以下结论成立:
1)CφIg:LB→LB是有界的当且仅当
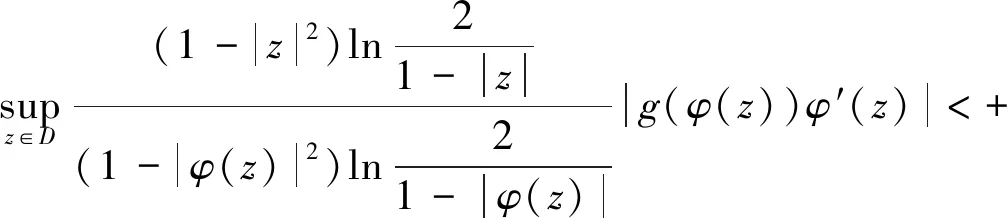
(5)
2)CφIg:LB0→LB0是有界的当且仅当式(5)成立且
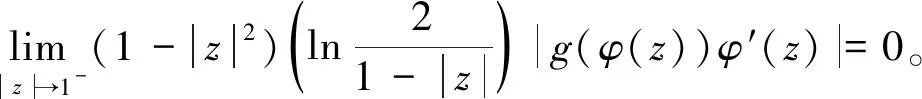
(6)
证明1)假定CφIg:LB→LB是有界的。取f(z)=z,易得出
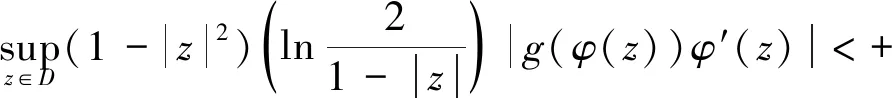
(7)
对∀0≠ω∈D,令
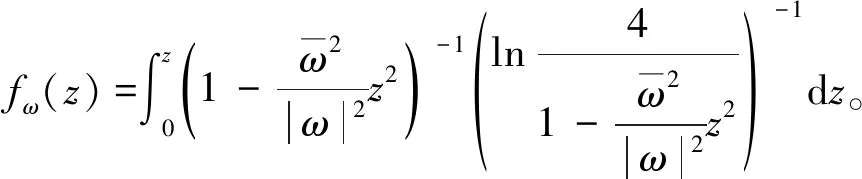
(8)
由引理3得
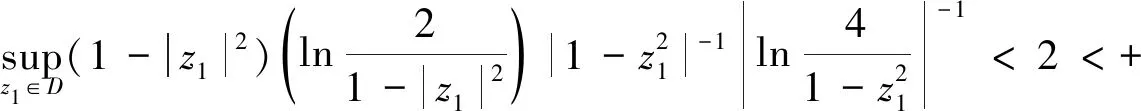

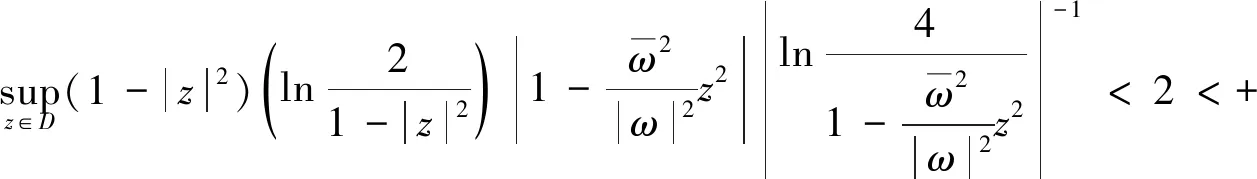
因此fω∈LB且‖fω‖L<4(ω≠0)。则对ω≠0得
‖CφIg(fω)‖LB≤‖CφIg(fω)‖L≤‖CφIg‖‖fω‖L<4‖CφIg‖<+∞。
(9)
所以对∀z∈D,φ(z)≠0,在式(9)中利用ω=φ(z),得到

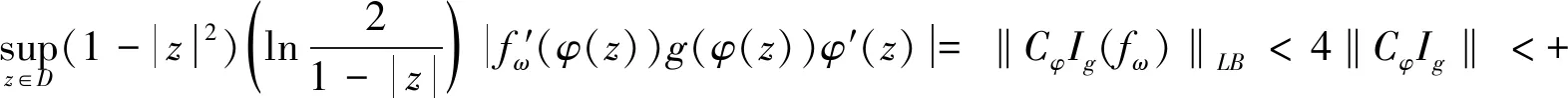
对∀z∈D,φ(z)=0,由式(7)得
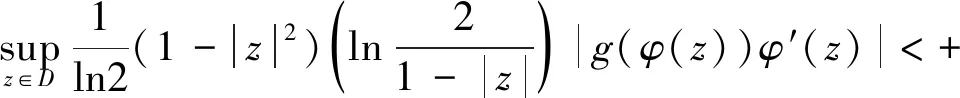
因此式(5)成立。
反过来,假定式(5)成立。对任意f∈LB,由引理1得:
并且
这表明CφIg是有界的。
2)假定CφIg:LB0→LB0是有界的。则由引理4知CφIg:LB→LB是有界的。再由1)表明式(5)成立。接下来,取f=z,易得式(6)成立。
反过来,给定f∈LB0。如果|φ(z)|→1-,当|z|→1-时,则由式(5),有
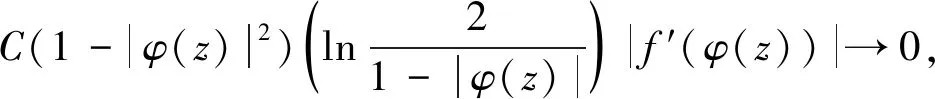
如果|φ(z)|≤r0<1,对每个z∈D。则由式(6)得
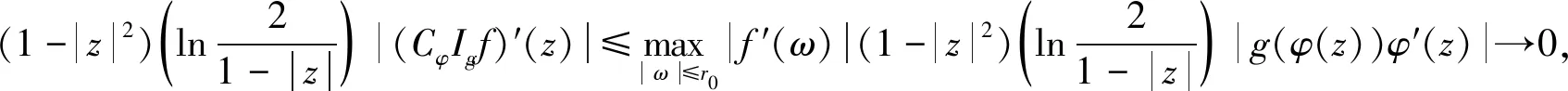
因此,对任意f∈LB0,有CφIgf∈LB0。又由1)得CφIg在LB上有界,所以CφIg在LB0上有界。
用定理3相同的方法可证得以下结论:
定理4令g∈H(D),φ是D上的解析自映射。则以下结论成立:
1)IgCφ:LB→LB是有界的当且仅当

(10)
2)IgCφ:LB0→LB0是有界的当且仅当式(10)成立且
由定理3和令φ(z)=z,可以得到关于Ig:LB(或LB0)→LB(或LB0)有界性的以下结论。
推论2令g∈H(D),则Ig:LB→LB是有界算子当且仅当Ig:LB0→LB0是有界算子当且仅当g∈H∞,其中H∞表示D上有界解析函数的代数。
由定理4和令g(z)=1,得到以下结论。
推论3令φ是D上的解析自映射。则以下结论成立:
1)Cφ:LB→LB是有界的当且仅当
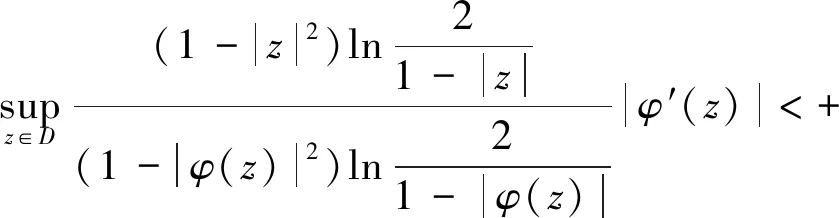
(11)
2)Cφ:LB0→LB0是有界的当且仅当φ∈LB0且式(11)成立。
3 结语
本论文经研究已得到了几类算子在对数Bloch空间上和小对数Bloch空间上有界的充要条件,但这几类算子在这两种空间上的紧性还未研究,这是接下来需要继续解决的问题和研究的方向。
