某型滑油冷却风扇振动特性分析

蔡思奇，贺玉龙

（西南交通大学 地球科学与环境工程学院，成都 611756）

风扇转子为滑油冷却系统内的高速旋转部件，因此对于风扇转子的设计，在气动性能达到设计需要的同时，还应确保其强度及结构动力特性达到安全工作的要求[1]。当转子自身的工作转速或者相关的激振频率与转子的固有频率相接近，就会引起共振从而造成因振动引起的转静子碰摩或叶片疲劳断裂等故障[2–3]，因此在转子设计研发过程中，对其进行振动特性分析避免引起共振是确保设备安全服役的重要环节。

对于试验件的振动特性分析较为广泛的方法为模态分析。模态分析过程可以分为试验模态分析与数值模态分析[4]。例如对于铝制薄盘利用ANSYS有限元分析软件进行模态分析，得到其各阶振型[5]。通过数值计算的方法计算材料发生位错状况的各阶固有频率及频率比等振动特性[6]。而基于模态动力学的数值方法同样被运用在对离心风机的振动特性研究中[7]。

在进行模态分析的过程中，研究者往往采取单一的试验或数值模态分析方式，它们各自有其优缺点及局限性，而两者结合的方式能够保障计算结果的可靠性。像旋转叶片那样存在预应力的结构，采用两者结合的方式更加可靠[8]。因此对于该风扇转子采用试验和数值模态分析结合的方式，考察风扇的振动特性，并与旧型号转子比较。为转子的设计及使用的安全性提供相关建议。

1 锤击试验模态分析

试验件实际安装状态为图1所示。

其实际安装于直升机主减速器输出轴上，由轴带动风扇转子工作，前后分别是与之配套的导向器与整流罩。试验中根据实际安装状况通过夹具固定实现模拟安装状态。

图1 试验件安装图

模态试验的基本环节包括激励、测量和分析[9]。试验采用锤击法激振进行多点激励，通过压电式加速度传感器采集响应信号，并通过低通滤波放大器及信号采集器对信号进行放大调理，最后通过分析软件进行数据后处理，最终得出风扇转子整体叶盘和单个叶片在安装及自由状态的各阶模态。试验系统图见图2。

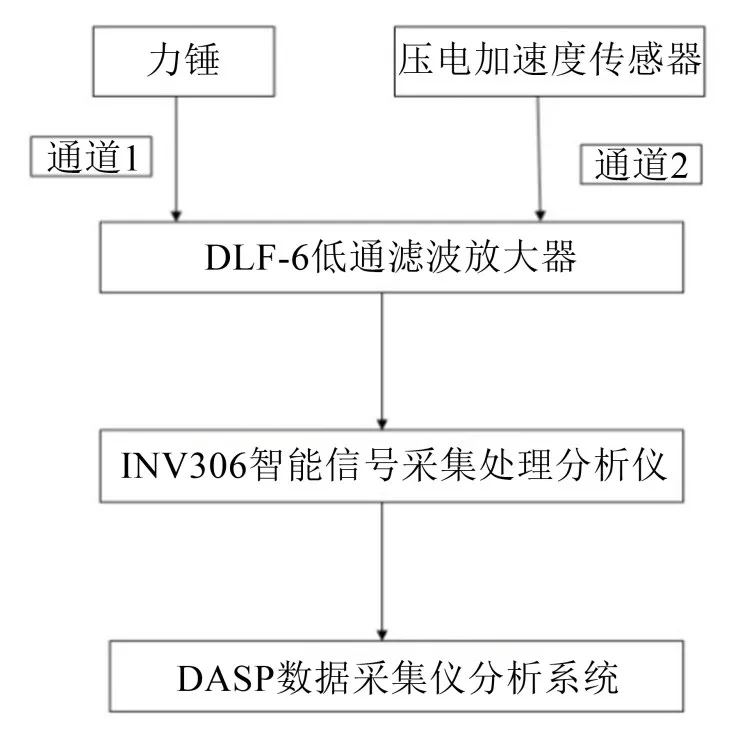
图2 试验系统图

试验得到安装及自由状态转子的模态振型，由于两种状态的转子模态振型相似，故仅列出安装状态振型如图3。

图3 安装状态各阶振型

从图3中可以发现，相对于轮盘部分，叶片的振动幅度更大，而叶片的振动以其扭转振动为主。

新型风扇转子及单个叶片的前4阶固有频率分别列于表1、表2。

无论是转子整体还是单个叶片，安装状态的前4阶固有频率及振型与自由状态下十分接近，说明转子与减速器输出轴固定连接对于其前4阶模态影响不大。叶片与转子整体前几阶的固有频率相差不大，而4阶呈现了较为明显的差异，轮盘质量与刚度相对叶片来说较大，且转子为整体叶盘结构，叶片与轮盘耦合可能是影响转子整体固有频率的因素。

表1 安装及自由状态转子固有频率/Hz

表2 安装及自由状态叶片固有频率/Hz

2 基于ANSYS的数值模态分析

由于风扇转子在工作过程中始终处于高速旋转状态，只对其静止状态进行模态分析无法考虑其自身转速对其影响，因此用有限元分析软件ANSYS对风扇转子静止和工作状态进行模态分析。

由于风扇转子叶片呈高度扭曲状态，直接在ANSYS内进行模型建立比较困难，因此借助NX软件建立计算模型，如图4、图5所示。

由于叶片呈19个均布状态，因此根据波动分析原理，在对风扇进行有限元分析时，可以取一个叶片-轮盘扇区计算[10]，如图6。

图4 风扇模型

图5 叶片模型

采用2阶单元Solid186用四面体网格对计算区域进行划分。网格单元数为59.8万个，节点数为13.7万个。在轮毂内环安装面上施加周向约束，在螺栓固定端面施加轴向约束。风扇整体采用材料锻铝2A70，其材料参数见表4。

从前5阶可以得到，叶片的振动幅度相对轮盘较大，前两阶振型为叶片的偏转，第34阶主要是叶片的扭转，5阶则为偏转与扭转复合振动。

图6 单个叶片-轮盘扇区

表4 2A70材料参数

静止状态下叶片的固有频率称为叶片的静频。得出其前5阶振动的静频值并提取其振型，如表5与图7。

表5 风扇各阶静频

为模拟转子在工作状态下自身转速对其各阶模态的影响，在计算时应考虑转速作为预应力，对转子施加转速0至8 000 r/min，及两个工作转速8 873和9 087转/分，并在计算时考虑陀螺效应。由于施加转速后得到的模态振型与静止状态相似，故不再列出。计算得出风扇转子的动频如表6。

图7 风扇各阶阵型

可以发现转子的动频与静频相比要高，并且随着转速上升呈逐步增加的趋势，这符合离心力的刚化效应。但总体随着转速增加固有频率的变化幅度很小，因此可以判定工作转速范围内预应力对于该转子固有频率的影响不大。由于转子工作时处于复杂的气动环境，除了其自身转速与固有频率重合会导致共振，还会受到外部其他激振力的影响，此处主要包括静叶流场不均引起的高频激振力与导向器加强筋所导致的低频激振力，由于此处低频激振力与固有频率线相距较远故仅考虑高频激振力的影响，前端静叶数为17，工作转速9 073 r/min对应的激振频率为2 574 Hz，根据表6与激振频率绘制坎贝尔图，判断共振转速，如图8。

从图8中可以得出，激励与各阶固有频率曲线的交点所对应的转速约为5 300 r/min与9 000 r/min左右，所预留的共振裕度很小。

由于叶盘属于循环对称结构，因此在计算中考察工作转速下节径的存在对于固有频率及振型的影响，如表7和图9。

节径所指的是如圆盘类的几何体在某阶振动模态振型中零位移的线。从计算结果发现，随着节径的增加，工作转速下转子的固有频率整体呈现增加趋势。此外出现的2阶固有频率相同，且位移也相近的状况，其差异主要是循环对称结构2阶模态存在着相位差。

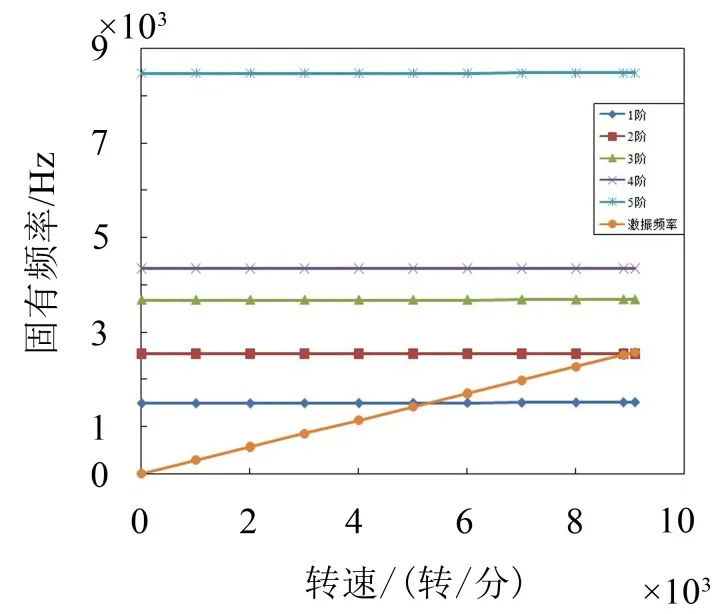
图8 新型转子坎贝尔图

由于在安装时，转子与机匣之间的间隙很小，故应考察在工作转速下叶片的最大形变量，避免转子与静子碰摩。根据图10，考察单个叶片-轮盘扇区在工作转速状态下的最大形变量及其发生的位置，可以得到最大的形变量为0.022 1 mm，最大形变发生在叶尖处。

为对比新旧型号冷却风扇转子在振动特性上的区别，对于旧型号转子同样进行数值模态分析，旧转子模型如图11所示。

表6 风扇各阶动频/Hz

表7 不同节径各阶固有频率/Hz

图9 工作转速各阶振型

图10 叶片-轮盘形变图

图11 风扇模型（旧）

同样根据数值模态分析结果绘制坎贝尔图，发现共振转速约为6 800 r/min，设计裕度达到19.5%，图12为根据旧型转子绘制的坎贝尔图。

根据图13，旧型号转子在工作状态下，即在转速为9 087 r/min下的最大形变量为0.049 6 mm，其产生的位置同样位于叶尖处。

通过对比新旧型号转子的振动特性，可以发现新型号转子其各阶固有频率相对旧型号偏高，这主要由于新型号在设计上鼓桶的直径增加，叶片的长度减小。此外由于设计时优先考虑风扇的性能要求，导向器静叶从13个增加至17个，因此新型冷却风扇由静叶尾端不均匀流场导致的高频激振力对应的共振转速与工作转速接近，容易引发振动。而新型号转子叶尖的最大形变量比旧型号要小55.4%，但两者的形变量都很小。

图12 旧型转子坎贝尔图

图13 旧型号叶片-轮盘形变图

3 结语

（1）通过试验模态和数值模态分析，分别得到不同状态下风扇转子的各阶固有频率，其工作转速远低于转子的1阶固有频率，在工作状态下不会引发自身的共振。而数值模态分析得到的数据与试验结果上略有差异。模态分析得到风扇各阶振型，相对于轮盘叶片的扭转及偏转为振动的主要表现形式。

（2）根据数值模态分析，转子的动频相对静频要略大，而其变化规律是随着转速的增加逐渐增加。新型号转子在振动特性方面较旧型号的各阶固有频率都要更高，而且叶尖的最大形变量更小。

（3）由风扇导向器静叶尾流所导致的高频激振力对于叶片振动的影响较大，这一点在改型后的结构中表现较为明显，激振力对应的共振转速与工作转速相接近。但由于激振力相对于转子自身工作转速与固有频率重合所造成的影响相比较小，而此冷却风扇系统改型以实现性能提升为首要目标，因此对于激振力的影响主要的应对措施是避免在使用过程中叶片出现裂纹等故障，此时激振力的存在会使叶片出现疲劳断裂等状况。因此使用过程中应定期对叶片的安全性进行检查，避免事故发生。

[1]李林蔚，高红霞，余建祖，等.某直升机主减速器滑油冷却系统设计[J].直升机技术，2008，156(4)：37-41.

[2]王树兰.某航空发动机振动故障诊断[D].长沙：湖南大学，2011.

[3]YAN XIAOJUN,NIE JINGXU.Creep-fatigue tests on full scale directionally solidified turbine blades[J].Journal of Engineering for Gas Turbines and Power,2008,130(4):044501.1-044501.5.

[4]梁君，赵登峰.模态分析方法综述[J].现代制造工程，2006(8)：139-141.

[5]F KLIMENDA,J SOUKUP.Modal analysis of thin aluminium plate[J].Procedia Engineering,2017,177:11-16.

[6]C SOBIE,L CAPOLUNGO,D L MCDOWELL,et al.Modal analysis of dislocation vibration and reaction attemptfrequency[J].Acta Meterialia,2017,134:203-210.

[7]张元禄，南国防.基于模态动力学的离心风机振动特性数值研究[J].噪声与振动控制，2017，37(2)：40-41.

[8]唐铃，尚柏林，高兴伟，等.某型发动机风扇叶片的损伤预测与振动分析[J].噪声与振动控制，2016，36(5)：164-168.

[9]丁继锋，韩增尧，马兴瑞.大型复杂航天器结构有限元模型的验证策略研究[J].宇航学报，2010(2)：547-555.

[10]A LAZARUS,B PRABEL,D COMBESCURE.A 3D finite elementmodelforthe vibration analysis of asymmetric rotating machines[J].Journal of Sound and Vibration.2010,329:378-379.