复杂阻抗吸声结构的大规模有限元声模态分析方法

李颖洁，王 焘，校金友，文立华

（西北工业大学 航天学院，西安 710072）

随着噪声污染受到人们越来越多的关注，在航空航天、汽车制造等领域中，为了降低内部环境的噪声，必须考虑相应的降噪设计。特别是在航天领域，航天器在发射起飞阶段通常要经受严重的气动力。气动噪声等恶劣的环境会导致航天器内电子设备、有效载荷以及整体结构的失效和破坏[1]。

工程中通常使用吸声材料或吸声结构来吸收入射声波的能量，从而达到降低噪声的目的[2]。使用多孔材料降低噪声效果显著，已经受到越来越多的关注[3–5]。目前，工程上一般将多孔材料作为常值阻抗边界进行处理，然而由于多孔材料的结构复杂，使得计算声场时需要考虑由多孔材料引入的复杂频变阻抗边界，特别是在低频范围，阻抗频变特性非常显著，此时将阻抗假设为常值的方法是不准确的[6]。试验证明许多吸声材料的阻抗都有着明显的频变特性[7]。

通过模态分析计算声模态和频率，是指导吸声结构设计、考核吸声性能的重要途径。对声阻抗为常数的情况，声模态分析是求解常规二次特征值问题，有限元方法多采用LANCZOS迭代或子空间迭代方法，计算效率高，且可用于大规模工程问题的计算分析。然而当考虑阻抗的频变性能时，声模态分析变为求解一般的非线性特征值问题，现有主流商用有限元分析软件（如ANSYS，NASTRAN）还不具备这项功能。

事实上，由于工程结构减振降噪技术的发展需求，非线性特征值问题的高效数值解法已成为近年来的一个国际研究热点[8–12]。经典的多项式近似法[8]以及改进方法[9]只能不断近似逼近原问题的系数矩阵；牛顿迭代法[10]以及相应的改进方法[11]都需要反复求解线性方程组，对于大规模问题，计算效率低。围道积分法（Contour Integral Method）是近年来发展起来的一种特征值问题数值解法。与前面所提的迭代方法不同，它可以一次性计算出复平面上一个闭曲线（围道）内的所有特征值，并且便于并行化[12–13]，因而受到广泛关注。但是，该方法计算结果受围道积分参数影响很大，容易出现虚假特征根。

本文作者最近在围道积分法的基础上提出了一种新型特征值问题的数值解法，记为RSRR（Resolvent Sampling based Rayleigh-Ritz projection method）。RSRR不仅可以用于标准特征值和广义特征值问题，也可用于一般的非线性特征值问题。它采用采样法构造特征空间，解决了围道积分法中矩积分法构造特征空间时高阶矩失效的问题[14]，并且构造特征空间的范围比矩积分法的范围更大，使特征解更精确，稳定性更好。同时，它还保留了围道积分法适于并行计算的优势[15]。

本文将RSRR法应用于含复杂阻抗边界的声场模态分析。基于有限元分析软件ANSYS，实现了RSRR，从而可将其用于一般复杂工程问题的建模、分析和后处理；通过典型算例验证了方法的正确性，并通过航天整流罩模型的大规模计算分析，验证了对实际工程问题的求解效率。本文方法和阻抗表达式无关，是一种通用的声模态工程分析方法。

1 频变阻抗非线性特征值问题

1.1 吸声材料的频变阻抗模型

工程上常用的吸声降噪的材料有蜂窝板、泡沫材料、玻璃纤维、玻璃棉、纤维毯等。不同材料的吸声特性不同。进行声学特性分析时，通常是将吸声材料等效为声场的阻抗边界条件。目前工程应用中普遍将由吸声材料引起的阻抗等效为常值进行计算，而实际上，吸声材料的阻抗是随频率变化而改变的。在低频范围，受频率影响很大。文献[16]通过试验得到玻璃纤维的阻抗-频率曲线如图1所示。可以看出，将阻抗等效为常值在低频范围会给分析带来很大误差。

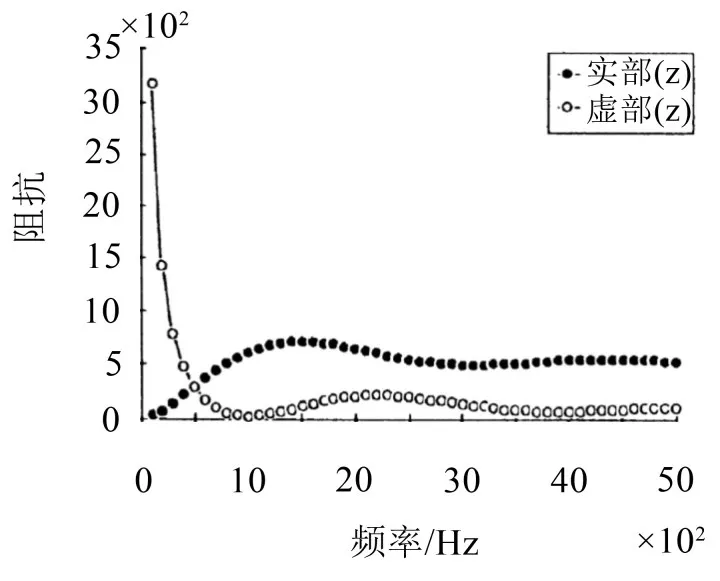
图1 玻璃纤维的声阻抗

下面分别介绍两种吸声材料的频变声阻抗模型。在第四节的算例中将考虑这两个模型。

Kelvin-Voigt模型：

Kelvin-Voigt模型采用一个简单的一维模型模拟声场表面多孔材料的声阻抗。阻抗随频率变化的表达式为

其中参数kI和dI分别表示吸声材料的弹性和粘性特性，ω为角频率，j为虚数单位。这两个参数通常可以进行实验或通过Biot-Allard理论得到。例如，对于图1所示的玻璃纤维的试验结果，可确定参数dI=50 Pa s/m ，kI=5×106Pa /m 。

Delany-Bazley模型：

Delany和Bazley对多孔纤维材料的阻抗特性进行大量的测量和研究，得到表面阻抗的表达式为

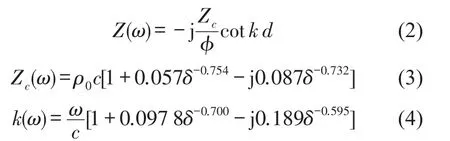
其中d是材料厚度，ϕ是孔隙率，Zc为材料特征阻抗，k为复波数，δ=ρ0ω/2πσ，σ是多孔材料的电阻率，ρ0是密度，c是声速。

Delany-Bazley模型在多孔吸声材料建模中应用很广。文献[7]中则通过实验验证了洋麻、大麻、椰肉、稻草等多种纤维吸声材料吸声性能的频变特性，且采用Delany-Bazley模型拟合了各种纤维材料的频变阻抗。

1.2 声学有限元模态分析

考虑三维声腔V，声腔内介质为理想的非粘性介质。频域内现行声学Helmholtz方程为[17]。

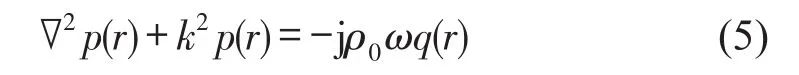
其中p(r)为声压函数，q(r)为体积速度函数，ρ0为声场密度，ω为角频率。声场边界为Ω。考虑一般情况，边界Ω由Dirichlet边界Ωp、Neumann边界ΩV和Robin边界ΩZ三部分组成，即Ω=ΩP⋂ΩV⋂ΩZ，相应的三种边界条件分别为

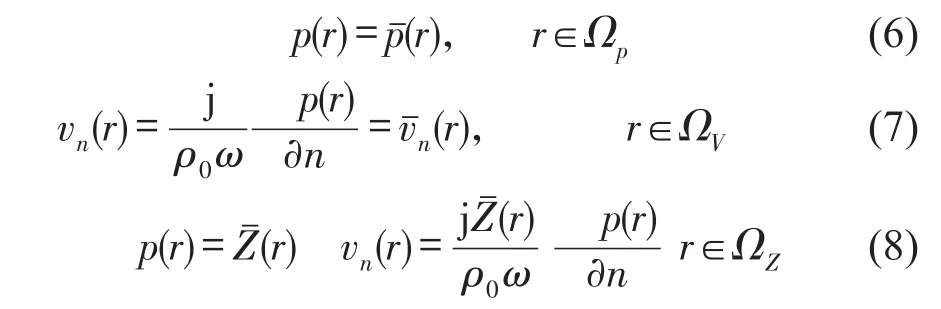
采用加权余量法，获得Helmholtz方程的等效积分弱形式，再将声场V进行单元离散，对场变量进行插值近似，则可得到纯声学有限元方程。

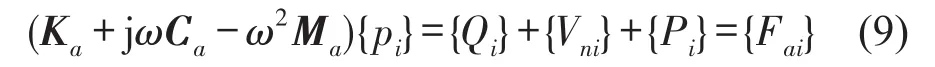
其中Ka为声刚度矩阵，Ma为声质量矩阵，Qi为声学激励向量，Vni为输入速度向量，Pi为输入声压向量。Ca为声阻尼矩阵，与边界声阻抗有关，i行j列的矩阵元素计算式为

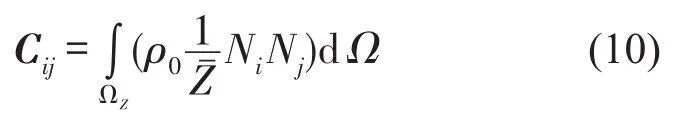
其中Ωz为阻抗边界。Ni、Nj分别为有限元形函数矩阵的第i行元素和第j列元素。模态分析时，式(9)中的激励为零，形成特征值问题

式中λ表示角频率ω，v表示声压向量{pi}

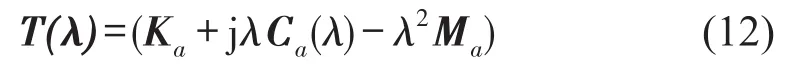
由阻尼矩阵的计算式可以看出，当阻抗为常值时，阻尼阵Ca则为常矩阵。声学特征值问题为常规二次特征值问题。而当声阻抗为频率的函数(ω)时，声学特征值问题的求解则转化为非线性特征值问题。虽然这类特征值问题在吸声降噪设计分析以及其他工程领域应用很广，但目前仍没有十分有效的大规模数值解法，主流商业有限元软件也不具备直接求解这类非线性特征值问题的模块。

2 RSRR算法

基于预解矩阵采样的瑞利里兹法(记为RSRR)是我们团队最近发展的非线性特征值问题的通用解法[15]。本节将该方法应用于特征值问题的数值求解，基于ANSYS声场分析模块，二次开发了复杂声场模态分析功能。下面首先介绍RSRR算法的基本原理，然后讨论在ANSYS软件中的数值实现方法。本文的实现思路在其他声学有限元分析软件中同样适用。

考虑非线性特征值问题T(λ)v=0，现欲求复平面内由简单闭曲线C围成的区域里面的所有特征值及其对应的特征向量。RSRR算法计算过程分为两步：一是采用预解矩阵采样法构造包含所有特征向量的特征空间S，取S的一组正交基为Q；二是基于Q采用经典Raylei-Ritz投影法，将原特征值问题转化为小型缩减特征值问题TQ(λ)g=0，并进行求解，其中，为Q的列数。缩减特征值问题的维数一般为几十至几百，属于小规模问题，现有许多方法都可以用于求解，如NEWTON法、修改的围道积分法[15]等。缩减特征值问题与原问题的特征值相同，对应的特征向量存在转化关系v=Qg。

2.1 特征空间的构造

RSRR算法中，特征空间的构造采用预解矩阵采样法，步骤如算法1所示。

算法1：预解矩阵采样算法

在采样点位置，采样点数目N，以及随机向量数目L选取合适的情况下，构造的空间S近似包含围道C内所有特征向量，原因如下。

根据Keldysh理论[15]，矩阵T-1(z)可由围道C内T(z)的特征值和特征向量表示

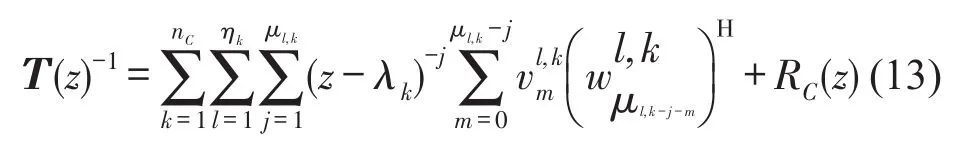
其中nc为互不相同的特征根数目，ηk表示非零空间的维度，μl,k表示λk的第l阶局部重数。和分别是T(λk)的右、左正规化广义特征向量，RC(z)表示围道C之外的所有特征值的贡献。由式可知，矩阵T(z)的特征值即为T-1(z)的极点。

构造特征空间的目的是，从式(13)中提取出特征向量VC。为此，首先将式写为如下矩阵形式

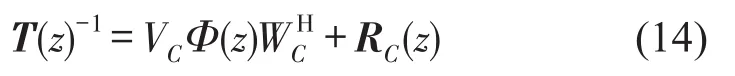
函数矩阵RC(z)代表围道C之外所有特征值的贡献，在围道C内部是解析函数。因此，可在一组给定的基函数gj(z)(j=1,…J)下展开成如下形式

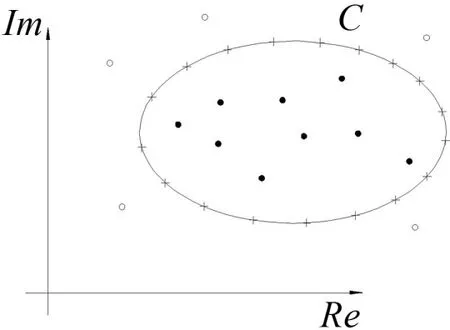
图2 采样围道示意图

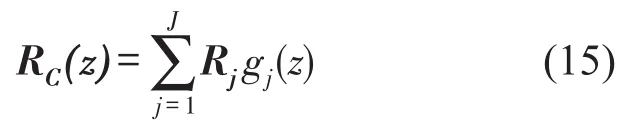
式中Rj是展开系数矩阵。常用的基函数有Lagrange多项式、Chebyshev多项式等；根据多项式逼近理论，对于解析函数，当插值点和基函数选取合适时，能获得指数收敛速度。而对于本文的特征空间构造方法，并不需要明确计算基函数，基函数的影响体现在采样点（即插值点）的选取上。比如，当C为一个实区间时，采样点可取为该区间上的Chebyshev点，相当于基函数gj(z)为Chebyshev多项式，式(16)的逼近精度很高。

随机矩阵U∈ℂn×L的作用是对T-1(z)进行探测，获取特征向量矩阵VC的信息。由T(z)矩阵Jordan标准型的矩阵结构可知[14]，U的列数L至少要等于矩阵T(z)在围道C内最大的特征根重数，即

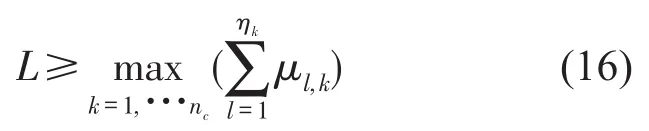
将式(15)代入式(14)之后，T-1(z)U可表示为

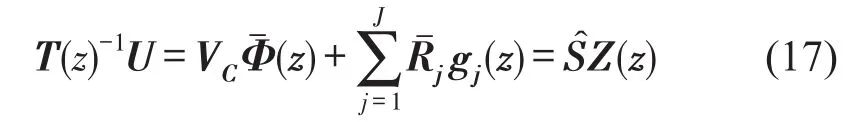
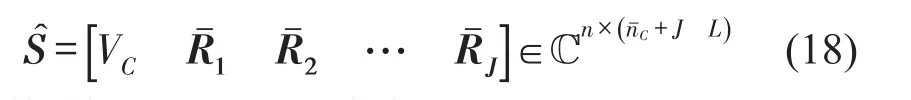
而矩阵Z(z)的表达式为

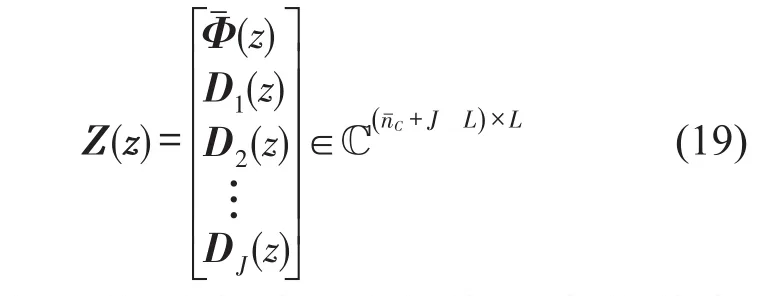
其中Dj(z)为L维对角阵，对角线元素的值都是gj(z)。

由式可知，特征向量VC包含在̂的列空间中，即

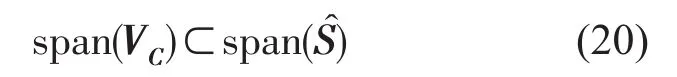
为有效提取出̂空间，本文选取N和采样点，形成采样解空间S

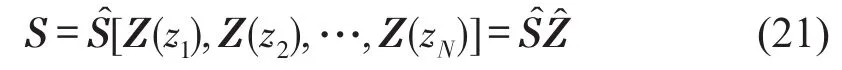
在瑞利里兹投影中需要S的正交基Q，可以通过S的截断奇异值分解（SVD）计算得到，即S≈QΣVH。由于S的列数N∙L通常很小，并且独立于问题的尺寸n。所以，SVD分解的计算量随n线性变化。令ks代表S经过SVD分解后的数值秩，要得到围道C内的所有特征值，则要满足ks≥rank(VC)。最后需要指出，当采样点距离特征值很近时，T(zi)-1U的数值会很大，为保证特征空间构造过程的稳定性，在SVD分解之前应先对矩阵S的列向量进行归一化处理。

2.2 算法的实现

采用RSRR算法求解非线性特征值问题的步骤如下。

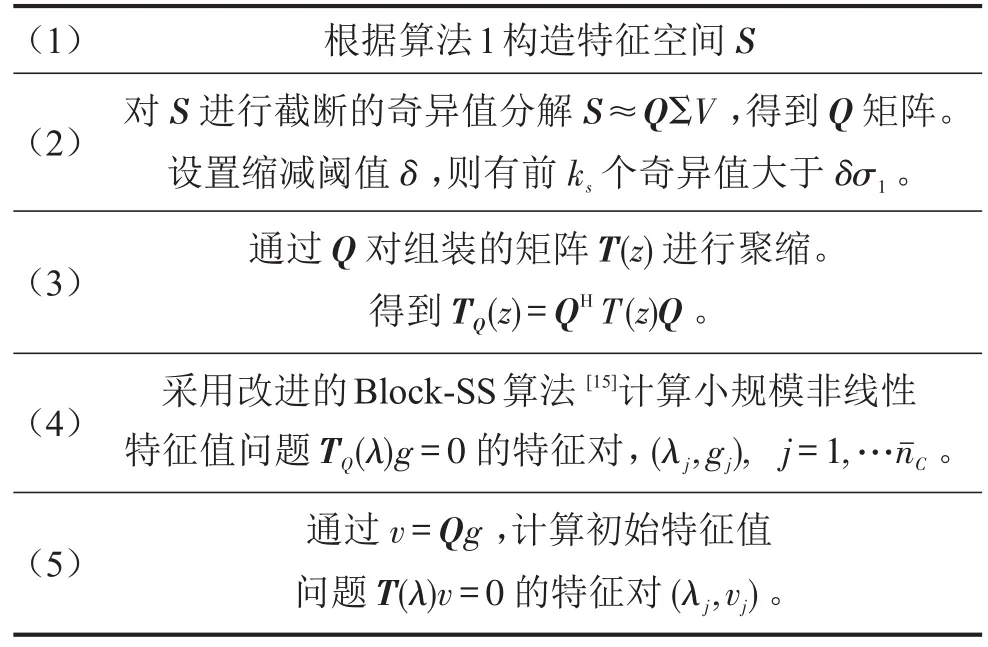
算法 2：RSRR算法

本文基于ANSYS的参数设计语言（APDL）实现了以上RSRR算法，最终以二次开发的形式在ANSYS软件中实现了考虑频变阻抗边界的声场模态分析功能。下面详述实现中的关键技术问题和处理方法。

物理建模在ANSYS前处理环境下进行。具体包括建立声场模型，划分网格和施加声场边界条件。由于ANSYS中对声场无法施加频变阻抗边界条件，故可将频变阻抗用任一常值阻抗代替，而在后面的二次开发程序中将其替换为频变表达式。ANSYS求解模块设置求解类型为模态分析，在求解有限元方程组之前中止，将质量矩阵Ma、刚度矩阵Ka和阻尼矩阵Ca导出到数据文件中。

RSRR算法参数的确定。实际应用中通常是欲求某个区间或复平面上某个区域内的特征值，据此可确定特征值搜索范围，边界围道C取椭圆或矩形较为方便。确定采样点数目N，需要对待求特征值的数目进行预估，由于此处对预估精度要求不高，可以通过常值阻抗时的特征值数目来估计。采样点可取为围道C上积分点或围道内Chebyshev点。L不小于最大特征根重数，这可以根据模型的对称性进行估计。计算经验表明，为保证特征根的计算精度，参数N∙L的选取应大于特征值数目的2～3倍。生成随机矩阵U∈ℂn×L之后，对其进行归一化有利于方法的稳定性。

构造特征空间Q时，首先将频变式(12)阻抗模型代入式(10)，从文件读入Ma、Ka和Ca并按式通过APDL Math重新计算T矩阵。调用ANSYS直接求解器，在每个采样点上计算T(zi)-1U。将求解结果组装成矩阵S。ANSYS中多波前法求解器的计算效率高、稳定性好，在ANSYS中进行这部分计算保证了本文特征值解法较高的总体计算效率。对S的截断奇异值分解可将MATLAB中的奇异值分解函数编译成.exe文件，在ANSYS中调用。分解之前对其列向量归一化，对保证方法的稳定性非常重要。奇异值截断阈值一般取为δ=10-14。

聚缩后小型特征值问题系数矩阵TQ的计算，主要是矩阵乘法运算，在ANSYS中进行。本文采用改进的Block-SS算法[15]求解小规模非线性特征值问题，其中的围道仍取为RSRR中的围道C。得到缩减特征值问题的特征对(λj,gj)。这个求解过程可通过MATLAB语言编程实现，并编译成.exe文件在ANSYS中调用。

3 算例

提供三个算例验证本文方法和ANSYS实现的正确性和计算效率。前两个算例中声场边界阻抗模型分别为第2.1节中的Kelvin-Voigt模型和Delany-Bazley模型，目的是和现有文献结果对比，验证本文方法的正确性。第三个算例对铺设吸声材料的火箭整流罩模型进行声模态分析，考察本文方法对于大规模问题的适用性和计算效率。所有算例均在一台32核（Xeon E5-2630 v3，2.40 GHz）64 GB内存的工作站上进行。线性方程组的求解均采用ANSYS软件中frontal直接解法，采用16核并行运算。

3.1 算例1

考虑文献[19]中尺寸为1 m×0.1 m×1 m的立方体声场。在z=1 m处根据式(1)设置阻抗边界条件，其中dI=50 Pa s/m ，kI=5×106Pa /m 。其余各面设置为刚性边界。声场介质为空气。本文空气密度均取为ρ0=1.2 kg/m3，声速均取为c=340 m/s。在有限元模型中，将声场划分为12 500个8节点6面体声场单元。

为了方便与文献[19]的解析解对比，本文计算50 Hz到350 Hz范围内的5个特征解及误差。RSRR方法采样点取在椭圆围道上，椭圆中心位于（200，0），椭圆长轴a=150，椭圆短轴b=0.1a。根据3.2节关于参数N和L取法的讨论，采样点N取10，L取2。

表1 常值阻抗与频变阻抗计算结果对比

RSRR方法求得的特征值见表1中第2列。此表第3列为文献[19]中提供的解析解，与本文结果基本相同，证明了本文数值计算结果的正确性。为考察特征值和特征向量的综合误差，还计算了5个相应特征对的相对误差||T(λ)v||2/||v||2，均在10-10以下。

进一步研究了考虑阻抗的频变特性对模态分析结果的影响。对文献[19]中的模型，在z=1 m的表面处施加Zs=104Pa s/m的常值阻抗进行计算，可得相应的特征频率如表1中第4列所示。与考虑频变阻抗的结果对比可知，将阻抗用常值代替会带来模态频率上的较大差异，这是因为500 Hz以下该吸声材料Kelvin-Voigt模型的阻抗变化很大，如图1所示。因此，对于阻抗频变较为严重且对特征值精度要求较高的情况，必须考虑边界阻抗的频变特性。

3.2 算例2

考虑文献[6]中的0.5 m×0.4 m×0.3 m立方体声场模型，在x=0.5 m处施加阻抗边界条件，阻抗模型为式(2)的Delany-Bazley模型，其中有关参数取值为d=20 cm 、σ=2×104Ns/m4、ϕ=1 和ρ0=1.2 kg/m3。其余边界为刚性边界。声场介质为空气，划分7 500个8节点6面体声场单元。

通过RSRR方法计算300 Hz～750 Hz频率范围内的八阶特征值以及相应的特征对误差。在矩形区域[200+0j；500+200j]边界取点。取N=30 ，L=1。计算所得结果与文献[6]进行对比。

由表2结果可见，对于较为复杂的阻抗模型，文献[6]中采用特殊积分法对阻抗模型进行2次近似时会带来一定的误差。而采用RSRR法求解复杂阻抗边界条件的声学特征值时，不需要对频变阻抗模型进行近似，所以更接近真实特征值，特征对的求解误差也均在10-11以下。因此RSRR方法求解此类复杂频变阻抗有限元声学特征值问题具有优越性。

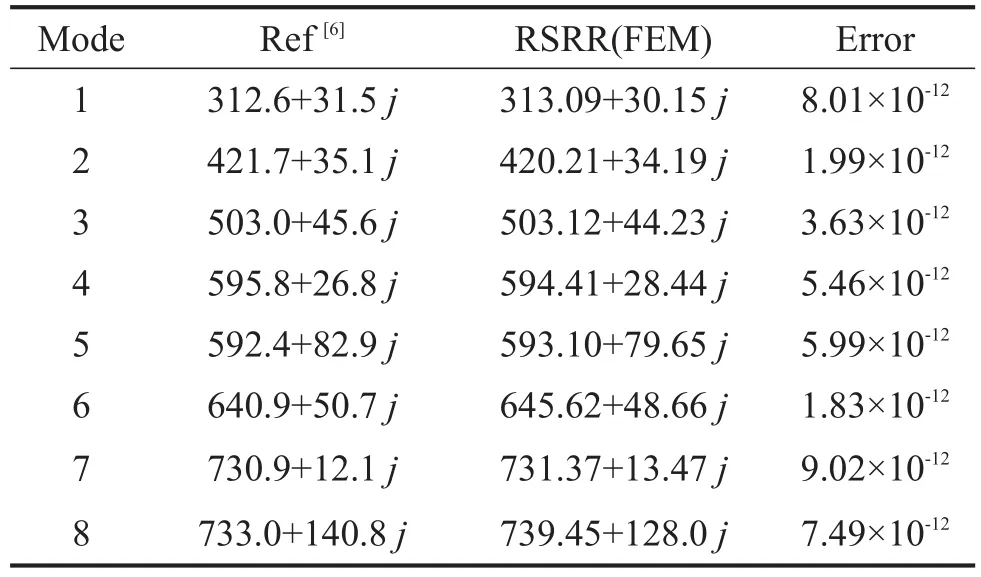
表2 Delany-Bazley阻抗模型的声学特征值求解

3.3 算例3

火箭整流罩结构的作用是保护航天器的有效载荷、降低噪声和振动的影响，为此通常在前锥和圆筒段铺设吸声材料以达到减振降噪的效果。本算例考虑图3所示的内部有卫星的整流罩内声场。整流罩轴向最大尺寸为2.288 m，径向最大尺寸为1.325 m。内部卫星轴向最大尺寸为0.95 m，径向最大尺寸为0.75 m。声场介质为空气，在整流罩内表面深色区域铺设多孔纤维吸声材料，阻抗模型采用Delany-Bazley模型，有关参数取值与算例2相同。其余边界为刚性边界。由于模型结构较为复杂，划分单元时混合使用4面体和6面体单元，有限元模型规模为1 129 819自由度。

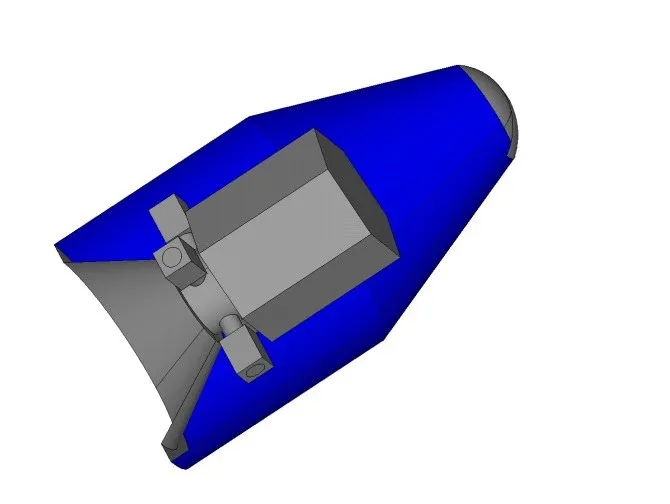
图3 考虑卫星的整流罩内部结构示意图

采用RSRR方法计算复平面矩形区域[200+0j，500+100j]内的所有特征值和特征向量。采样点取为该区域内的Chebyshev点，设N=102、L=2；采样点分布如图4所示。

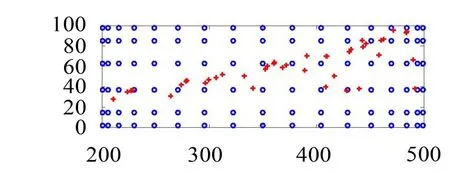
图4 采用RSRR计算有限元离散的铺设多孔材料的整流罩内声场特征频率（o表示采样点，+代表求得的特征值）

RSRR方法共求得50个特征对，整个求解过程耗时约9.4 h，占用内存26.7 GB，特征值分布如图4所示，特征对的相对误差如图5所示。

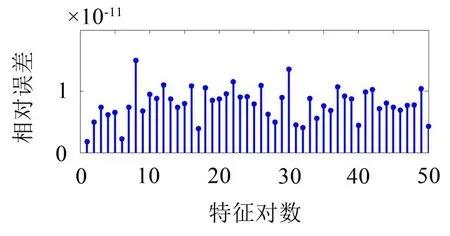
图5 整流罩特征根的求解误差

图6给出了计算所得前4阶声压模态及相应的特征频率。

该算例表明，采用RSRR方法求解含复杂阻抗边界的大规模声模态分析问题，仍具有较高的计算效率和精度。

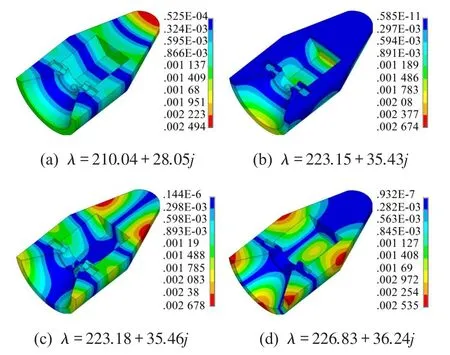
图6 整流罩前4阶模态图

4 结语

本文将新型非线性特征值问题数值解法RSRR应用于有限元声模态分析中，解决了现有商用有限元软件不能进行复杂频变阻抗边界的声模态分析问题。

基于RSRR算法，在ANSYS中采用样本法构造特征向量搜索空间，采用此特征空间对原大规模非线性特征值问题进行瑞利里兹投影，使原问题转化为小型非线性特征值问题，采用改进的Block-SS算法进行求解。采用采样法构造特征空间，既简化了计算过程，又使得结果更精确。本文的方法可以稳定高效地求解复杂阻抗边界的声学特征值，并且可用于大规模工程问题的计算。最后通过算例验证了此方法的准确性和通用性。

[1]陈钊.火箭整流罩内声场分析及降噪技术研究[D].哈尔滨：哈尔滨工业大学，2015.

[2]陈克安.有源噪声控制[M].北京：国防工业出版社，2014.

[3]裴春明，周兵，李登科，等.多孔材料和微穿孔板复合吸声结构研究[J].噪声与振动控制，2015，35(5)：35-38.

[4]王营，赵武，黄丹.多孔材料声学模型及其应用[J].材料导报，2015，29(5)：145-149.

[5]屈伸，陈浩然.敷设多孔吸声材料声腔特征值分析的径向积分边界元法[J].计算力学学报，2015(1)：123-128.

[6]LEBLANC A,LAVIE A.Numericalanalysisof eigenproblem for cavities by a particular integral method with a low frequency approximation of surface admittance[J].Journal of the Acoustical Society of America,2012,131(5):3876-3882.

[7]BERARDIU,IANNACEG.Predictingthesound absorption of natural materials:Best-fit inverse laws for the acoustic impedance and the propagation constant[J].AppliedAcoustics,2017,115:131-138.

[8]LARBI W,DEÜ J F,OHAYON R.A new finite element formulation for internal acoustic problems with dissipative walls[J].International Journal for Numerical Methods in Engineering,2010,68(3):381-399.

[9]EFFENBERGER C.Robust successive computation of eigenpairs for nonlinear eigenvalue problems[J].SIAM J MatrixAnalAppl,2013,34(3):1231-1256.

[10]NAKA Y,OBERAI A A,SHINNCUNNINGHAM B G.Acoustic eigenvalues of rectangular rooms with arbitrary wall impedances using the interval Newton/generalized bisection method[J].Journal of the Acoustical Society ofAmerica,2005,118(6):3662-3671.

[11]VAN BEEUMEN R,MEERBERGEN K,MICHIELS W(2015)Compact rational Krylov methods for nonlinear eigenvalue problems[J].SIAM J Matrix Anal Appl,36(2):820-838.

[12]LEBLANC A,LAVIE A.Solving acoustic nonlinear eigenvalue problems with a contour integral method[J].Engineering Analysis with Boundary Elements,2013,37(1):162-166.

[13]XIAO J,ZHOU H,ZHANG C,et al.Solving large-scale finite element nonlinear eigenvalue problems by resolvent sampling based Rayleigh- Ritz method[J].Computational Mechanics,2016:1-18.

[14]YOKOTA S,SAKURAI T.A projection method for nonlinear eigenvalue problems using contour integrals[J].Jsiam Letters,2013,5:41-44.

[15]XIAO J,MENG S,ZHANG C,et al.Resolvent sampling based Rayleigh-Ritz method for large-scale nonlinear eigenvalue problems[J].Computer Methods in Applied Mechanics&Engineering,2016,310:33-57.

[16]LADEVEZE P,ZIENKIEWICZ O.New advances in computational structural mechanics[M].1992.

[17]李增刚，詹福良.Virtual.Lab Acoustics声学仿真计算高级应用实例[M].北京：国防工业出版社，2010.

[18]XIAO J,ZHANG C,HUANG T M,et al.Solving largescale nonlinear eigenvalue problems by rational interpolation approach and resolvent sampling based Rayleigh-Ritz method[J].International Journal for Numerical Methods in Engineering,2016.

[19]BERMÚDEZA,RODRÍGUEZR.Modellingand numericalsolution ofelastoacoustic vibrationswith interface damping[J].InternationalJournalfor Numerical Methods in Engineering,1999,46(10):1763-1779.