基于区间摄动法的不确定结构高频动响应预示

宋海洋，张文正，张丰收，吕 稀，冯志鹏

（中国核动力研究设计院 核反应堆系统设计技术重点实验室，成都 610213）

新型工程产品和项目在研制初期一般都需要获得相应的声振环境预示数据，在低频段可以采用传统的有限元法或边界元法，但在高频段由于模态十分密集，重叠率高使得传统的有限元法应用起来十分困难。20世纪60年代发展起来的统计能量分析方法可以克服传统模态分析方法所遇到的这些困难，为解决复杂系统的高频振动及噪声问题提供了有力工具。

利用统计能量分析方法对工程结构的高频振动和噪声进行预示时，内损耗因子和耦合损耗因子等参数的测量精度对响应预示结果的精确性有着很大的影响。目前大部分都采用实验测量的方法来获得结构的内损耗因子和耦合损耗因子[1–3]，但是根据前人所做的大量实验和所获得的工程经验可知，对于大部分工程结构来说，内损耗因子和耦合损耗因子一般都是10-2～10-4量级的小数，在实际工作中想要对这些小数进行精确运算和测量是比较困难的[4–5]，最终的测量数据通常存在误差，而参数测量误差的积累会导致预示出的高频响应和响应的真实值之间存在偏差，目前尚未有相关文献报道关于参数的测量误差对预示结果影响的研究。

本文在考虑参数以及外载荷测量误差的前提下，结合区间摄动方法推导出了统计能量分析子系统的模态能量区间，利用模态能量区间可进一步获得不同频率点处的总能量区间。总能量区间的均值代表不考虑参数和外载荷测量误差时预示的动响应，而总能量区间上下界则反映了参数以及外载荷的测量误差对响应预示结果的影响程度。

1 区间的定义和运算

在区间分析中，不确定性变量可以用一个封闭的和有限的区间来表示。一个区间变量xI可以由它的区间下限xl和区间上限xu来定义，具体的表达形式可以写为[6]

本文使用上标“l”代表区间变量的下限，使用上标“u”代表区间变量的上限，同时使用上标“c”代表区间变量的均值，区间xI的均值定义为

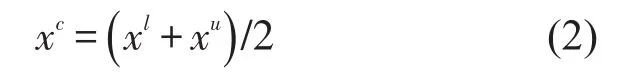
区间xI的离差定义为

两个区间变量xI和yI之间的运算规则如下[7]

2 统计能量分析功率流平衡方程

2.1 子系统间功率流

在统计能量分析理论中，子系统所储存的能量通过两种方式流出，一是子系统本身的能量耗散，能量被转化成热能等其它形式，二是能量从一个子系统传递到了另一个子系统。第i个统计能量分析子系统的损耗功率pid可用下式进行计算

其中f代表分析带宽Δf内的中心频率，Ei代表子系统i在频率点f处的总能量，ηi是子系统i的内损耗因子，它表示子系统i自身耗散能量的能力大小。

子系统i到子系统j的功率流为

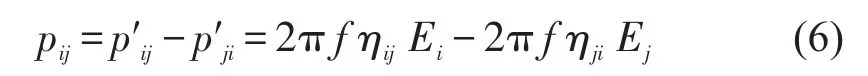
其中ηij和ηji是子系统间的耦合损耗因子，它们代表能量在子系统i和子系统j之间的传递效率。

统计能量分析中的耦合损耗因子和模态密度存在一个互易关系

其中di表示子系统i的模态密度。

2.2 功率流平衡方程

假设一个统计能量分析系统被划分为k个相互耦合的子系统，如图1所示

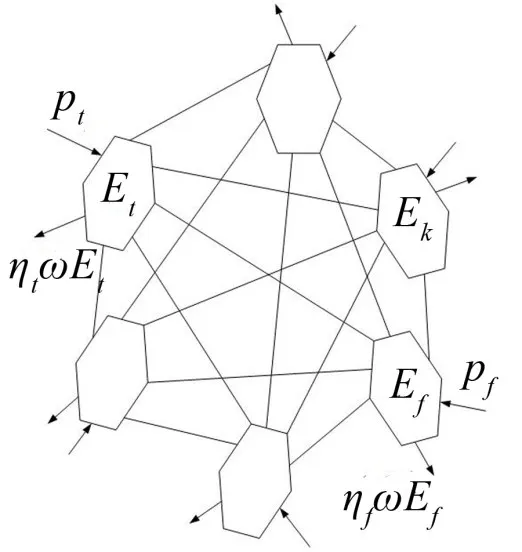
图1 k个相互耦合的统计能量分析子系统

由式(5)和式(6)可得子系统i的功率流平衡方程

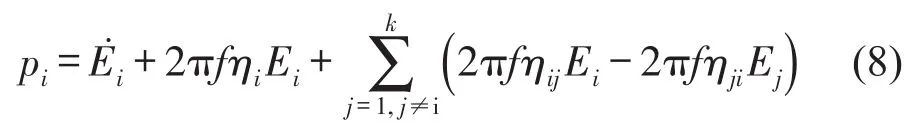
其中pi代表子系统i的外部激励源对子系统i的输入功率。为子系统i的能量Ei的变化率。本文研究的是稳态振动情况所以即子系统能量不随时间而变化。

利用式(7)给出的互易原理，将所有子系统的功率流平衡方程写成矩阵形式如下

其中N是一个包含模态密度di(i=1,2,…,k) 、内损耗因子ηi(i=1,2,…,k)和耦合损耗因子ηij(i,j=1,2,…,k)的k×k阶系统矩阵，f是分析带宽Δf内的中心频率，为计算方便令Pi=pi/πp f，ei(i=1,2,…,k)称为模态能量指的是在分析带宽内每阶模态所具有的能量。统计能量分析功率平衡方程是在分析带宽内各阶模态所具有的能量相等的假设下建立的，子系统i在各频率点处总能量Ei和模态能量关系为

3 基于区间摄动法的稳态响应区间计算

3.1 子系统模态能量摄动分析

利用式(9)，子系统的模态能量向量可以通过系统矩阵N的逆阵和功率向量P的乘积来获得

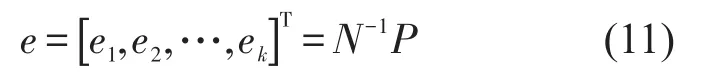
根据摄动理论，当系统矩阵N存在一个摄动量ΔN，功率向量P存在一个摄动量ΔP时，摄动法的平衡方程可以表示为

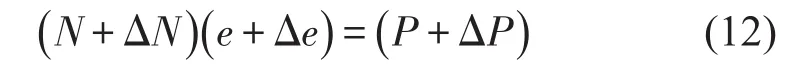
e+Δe能被进一步写为

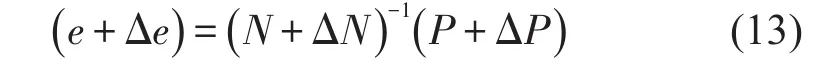
当矩阵范数 ‖N-1+ΔN‖小于1时，可以利用纽曼级数将(N+ΔN)-1展开如下

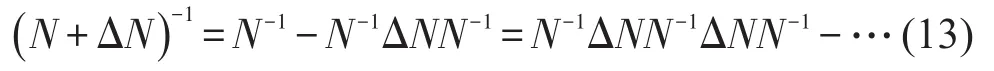
将式(14)代入到式(13)中得到

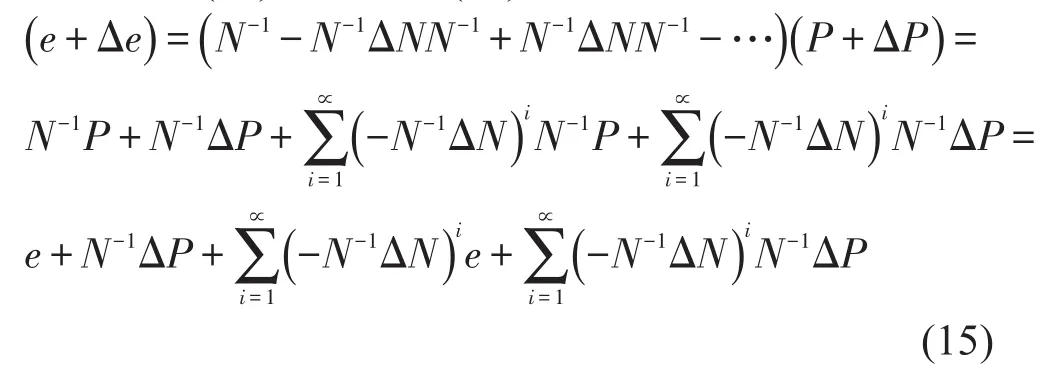
忽略式(15)的高阶微量，可以得到模态能量向量的摄动量为

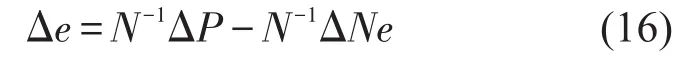
3.2 带有测量误差参数的区间表示

用实验测量的方式来获取结构的内损耗因子、耦合损耗因子和输入功率时，测量结果通常存在一定量的误差，下面采用式(1)的区间形式来表示带有测量误差的参数和输入功率

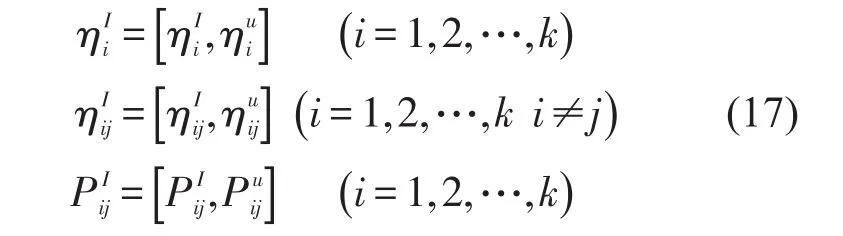
内损耗因子、耦合损耗因子和输入功率的测量值是式(17)的区间均值即，假设测量误差不超过±s%，则式(17)可以进一步写成

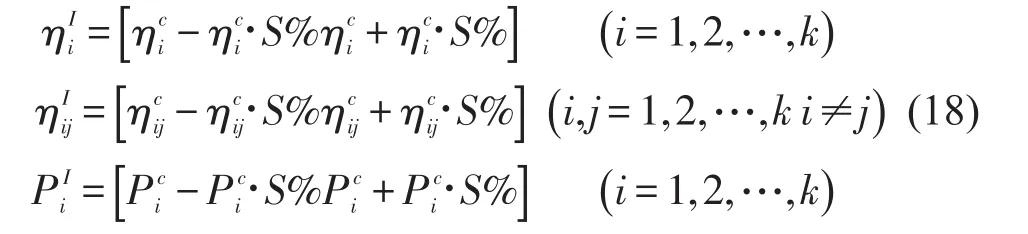
相比于内损耗因子和耦合损耗因子的测量精确性，模态密度的测量结果相对精确很多。再者任何区间分析方法都存在区间扩张问题，即过多的区间相乘或相除运算会导致最终的计算结果不精确。综合以上两方面原因，将子系统的模态密度处理成常数而不是区间变量。

3.3 子系统模态能量区间

本节将带有测量误差的内损耗因子、耦合损耗因子和输入功率(即式(17))代入到统计能量分析的功率流平衡方程，最终可以得到子系统模态能量区间，区间均值是不考虑参数和输入功率误差时预示的模态能量，而模态能量区间的上下限反映了参数和输入功率的测量误差对预示结果的影响程度和大小。将式(17)代入到式(9)中得区间形式的功率平衡方程为

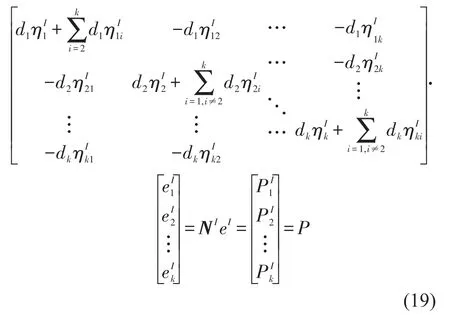
这里NI称作区间系统矩阵，它是一个包含模态密 度di(i=1,2,…,k)，内损耗因子区间和耦合损耗因子区间的矩阵，是子系统i的模态能量区间。

用区间均值和不确定区间来表示式(19)中的区间系统矩阵和区间输入功率向量

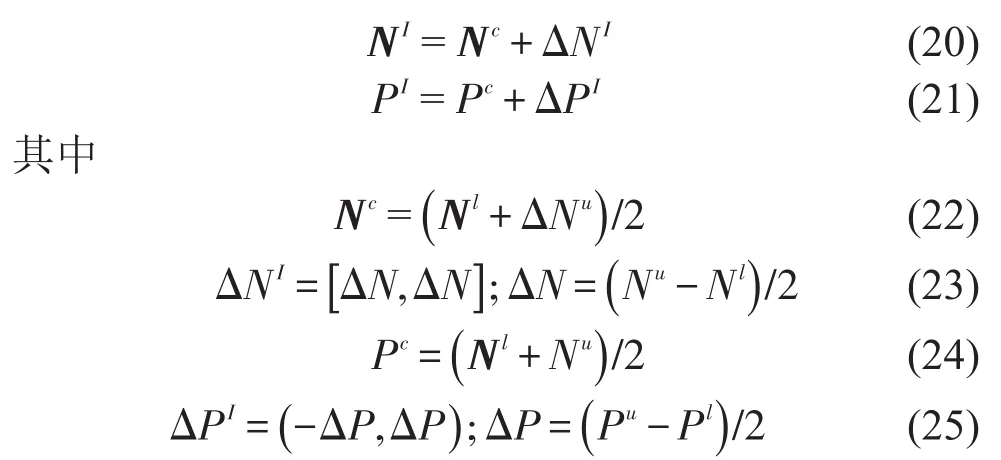
将式(20)和式(21)代入到式(19)中得到

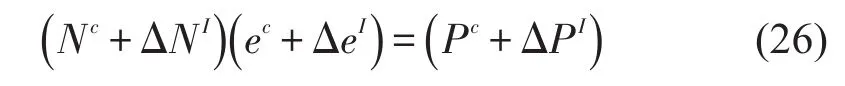
ΔNI可以看作是围绕Nc的一个摄动，而ΔPI可以看作是围绕Pc的一个摄动，这样就可以将式(26)看作是一个摄动形式的方程即

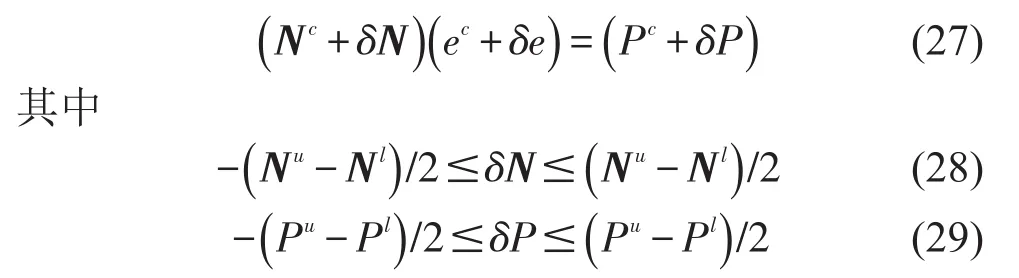
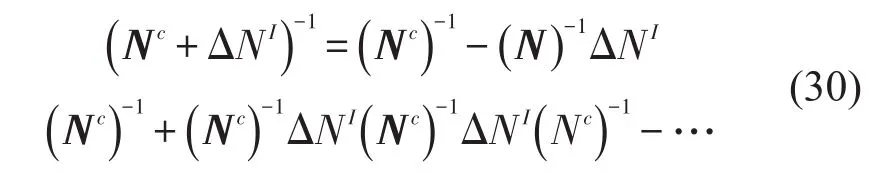
将式(30)代入到式(26)中得到

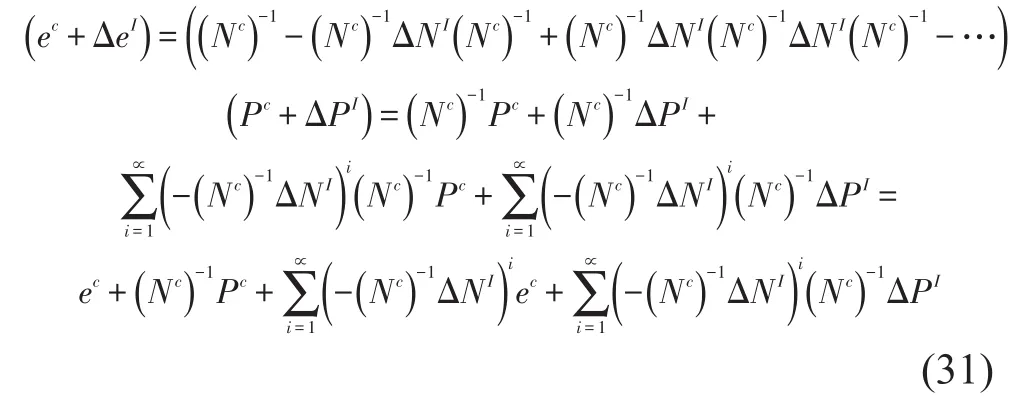
根据式(31)可以获得子系统模态能量的区间向量为

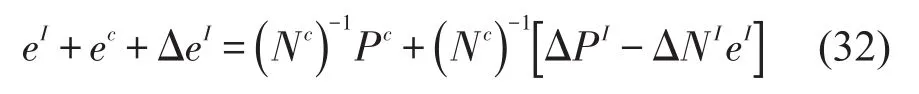
基于式(19)的区间功率流平衡方程，式(32)中的Nc和ΔNI可以表示为

假设Nc的逆矩阵为

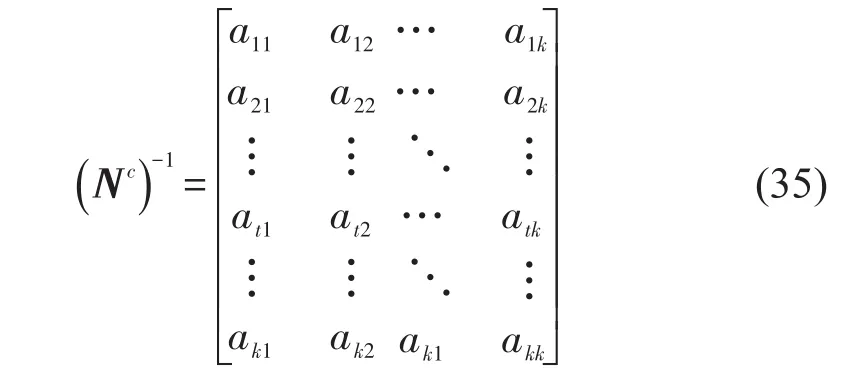
将式(34)和式(35)代入到式(32)中得

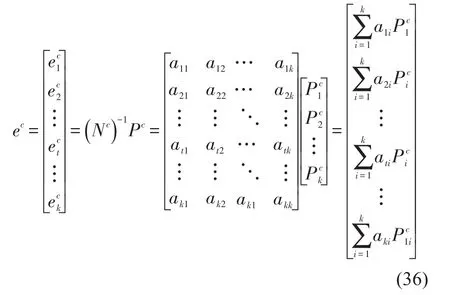
将式(36)和式(37)相加，最终可以得到任意一个子系统t(t=1,2,…,k)模态能量区间的上界和下界的计算公式

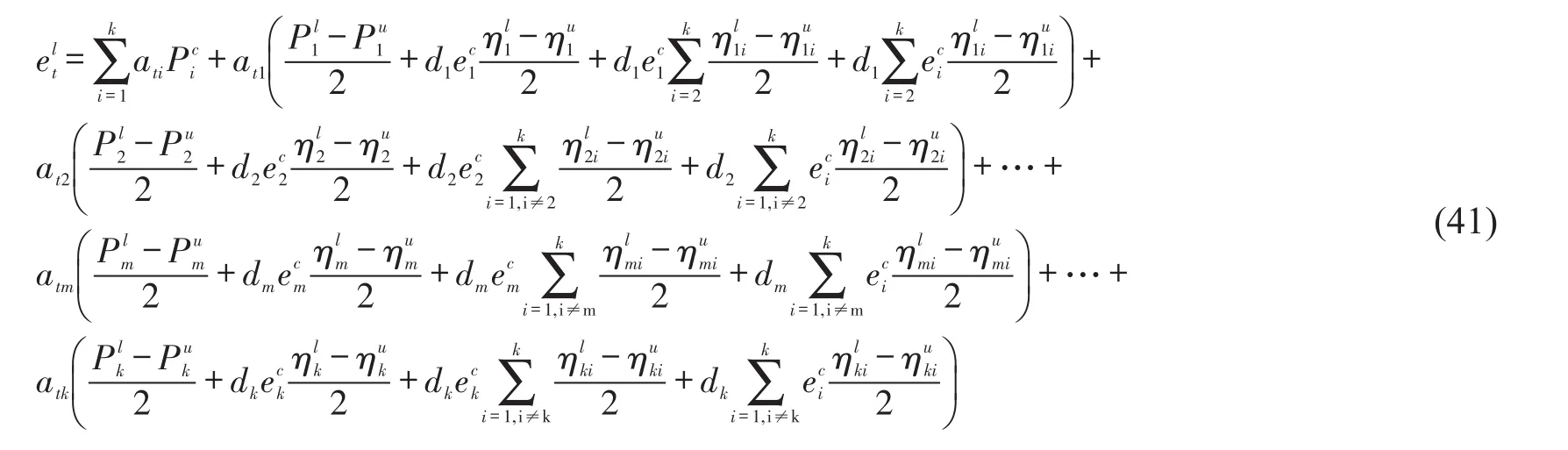
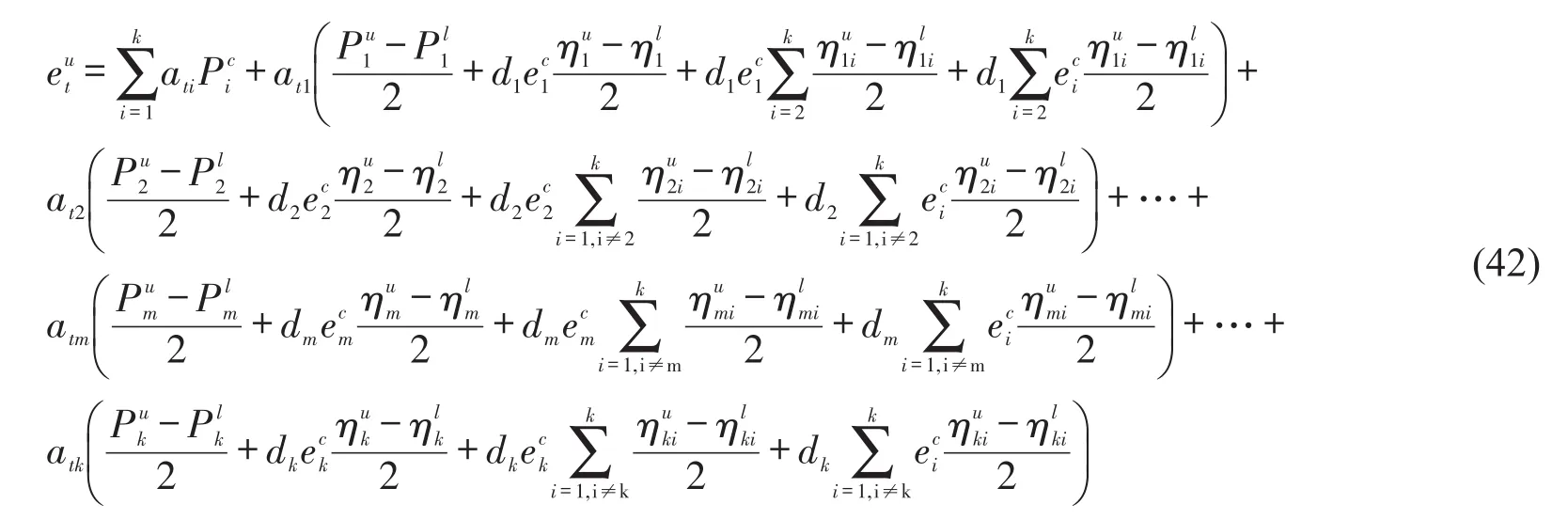
4 实验验证

图2是两块垂直相连的复合板结构，本节引用文献[8]针对图2典型板结构的振动实验结果，并将该振动实验结果与利用区间方法预示得到的响应结果进行对比。

图2 实验现场图[8]

右侧板1的长度为400 mm，宽度为500 mm，左侧板2的长度为600 mm，宽度为500 mm，复合板整体厚度为1.2 mm。两块复合板被划分为两个统计能量分析子系统，板1为子系统1，板2为子系统2。两个板分别布置了10和15个加速度传感器，每个板布置5个激振点。依次对各个激振点激励并测量激振力和激振点的加速度响应，对于稳态实验数据，由阻抗头测量的加速度信号的互谱密度函数计算稳态输入功率，由各板加速度信号的自谱密度函数的平均计算子系统的总能量，然后将子系统总能量和输入功率的比值作为归一化的总能量。

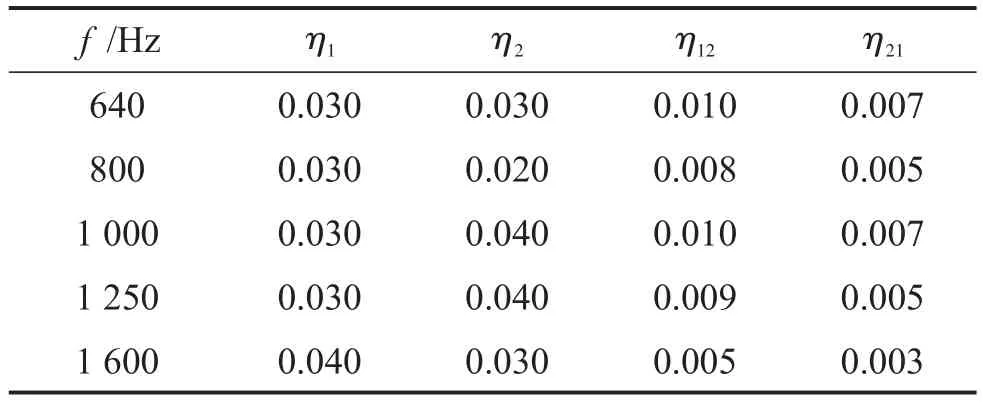
表1 两块板的内损耗因子和耦合损耗因子

假设表1中数据的测量误差不超过±8%，那么根据式(17)和式(18)的定义，可以将所有带有测量误差的参数都写成区间形式，其中区间的均值就是实际的参数测量值。

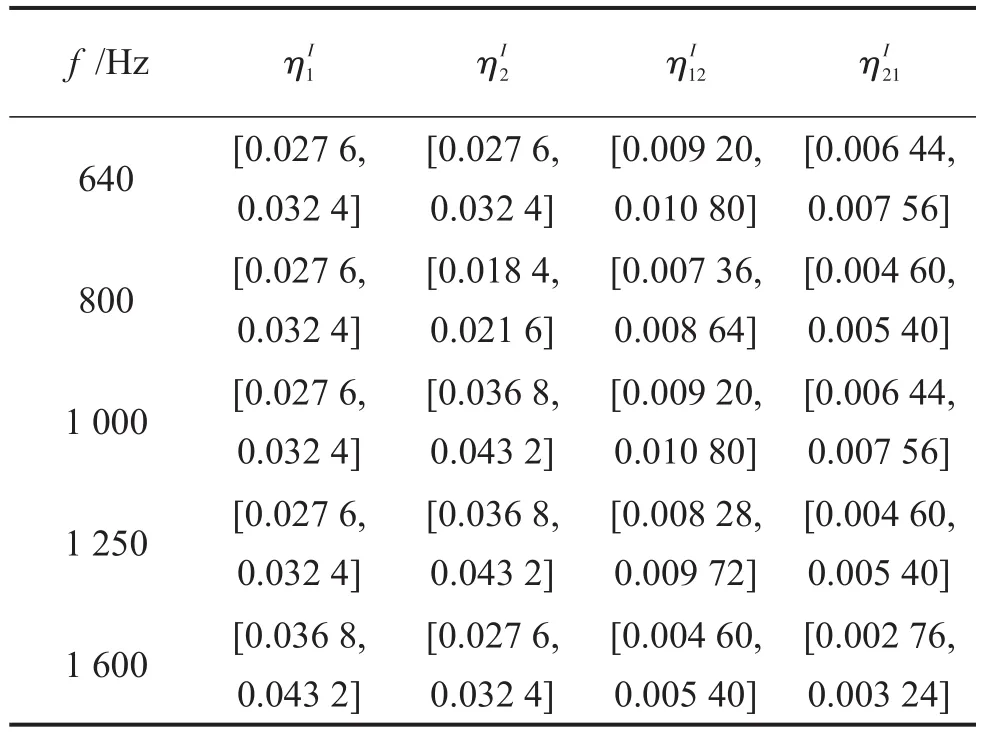
表2 用区间形式表示带有测量误差(不超过±8%)的参数

当统计能量分析的参数区间确定以后，需要验证一下是否满足式(30)的收敛条件，即矩阵范数小于1。

当分析带宽的中心频率为640 Hz时，可得

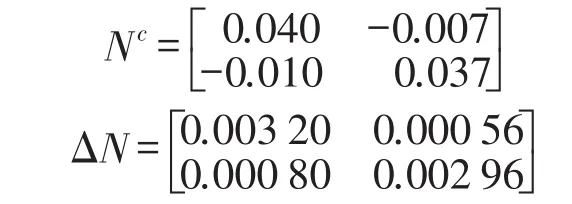
经计算可得两板的总能量区间如图3和图4所示。

图3和图4给出了由三种方式得到的板振动总能量：

(1)在考虑所有内损耗因子测量误差、耦合损耗因子测量误差以及外载荷测量误差的情况下，由本文提出的区间方法从理论上预示出的板总能量区间值；

(2)在不考虑任何内损耗因子测量误差、耦合损耗因子测量误差以及外载荷测量误差的情况下，由非区间的传统方法从理论上预示出的板总能量确定值(即区间均值)；

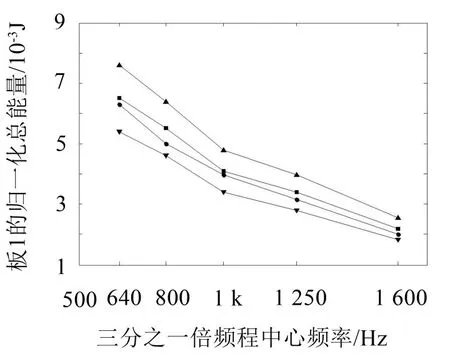
图3 板1在各频率点上的总能量区间

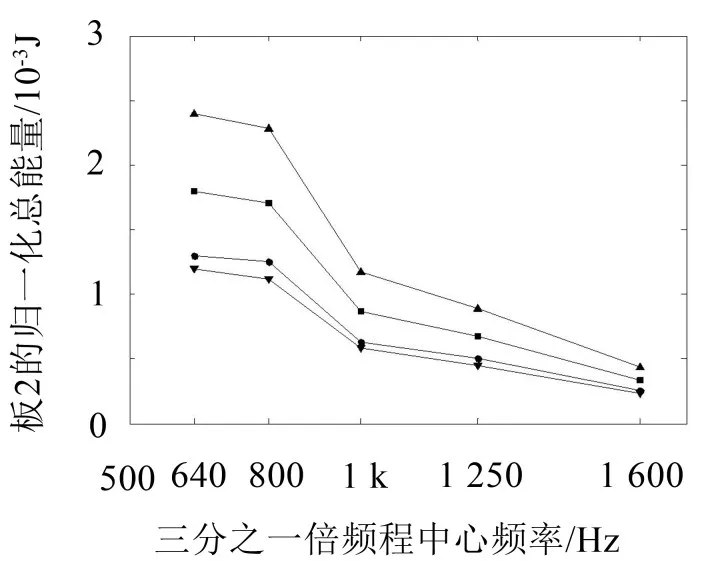
图4 板2在各频率点上的总能量区间

(3)由实验测量得到的板总能量。

图3和图4中的横坐标选取的是统计能量分析理论1/3倍频程的几个中心频率点，在统计能量分析理论中用中心频率点处的能量来代表分析带宽内能量的一个平均值，比如中心频率640 Hz的下限和上限频率分别是596 Hz和716 Hz，那么在统计能量分析中以640 Hz点处的能量代表从596 Hz到716 Hz带宽内的一个平均能量。由图3和图4可见板结构的总能量区间包含着总能量的真实值(即实验测量值)。

为了更具体地衡量参数和外载荷的测量误差对稳态响应预示结果的影响程度，定义

基于图3和图4给出的考虑参数和载荷测量误差时预示得到的板总能量区间上下限以及不考虑任何参数和载荷测量误差时预示得到的板总能量的确定值(即区间均值)，现给出由参数和外载荷的测量误差所导致的稳态响应的误差值如表3。

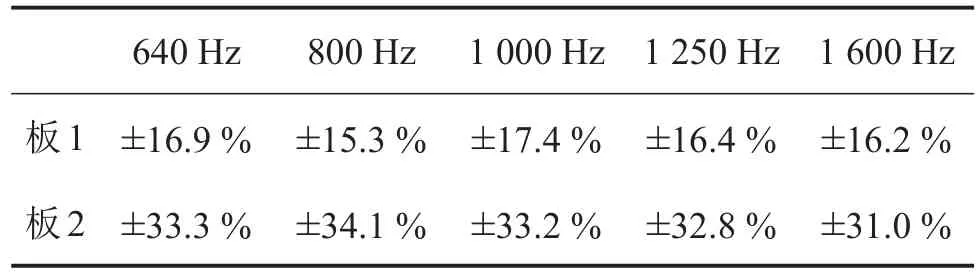
表3 由参数和载荷的±8%测量误差所导致的稳态响应误差

5 结语

对于复杂的工程结构在应用稳态统计能量分析方法预示高频段动响应时，往往并没有考虑到参数和外载荷的测量误差，导致最终的动响应预示结果不够精确，给后续的结构设计带来不准确的信息，所设计出来的结构也会存在一定的安全隐患，在实际恶劣的声振环境下破坏或者失效，因此在进行动响应预示时有必要考虑到参数以及外载荷的测量误差对预示结果的影响。本文考虑到稳态统计能量分析模型中损耗因子和外载荷的不确定性，将带有测量误差的内损耗因子和耦合损耗因子等参数以区间变量形式表示。通过求解统计能量分析区间功率流平衡方程获得了每个子系统的总能量区间，通过这个总能量区间可以得到参数和外载荷的测量误差对预示响应的影响程度和大小，为后续的结构安全和可靠性设计提供参考。

[1]PANUSZKA R,WICIAK J,IWANIEC M.Experimental assessment of coupling loss factors of thin rectangular plates[J].Archives ofAcoustics,2005,30(4):533-551.

[2]EWING M S,DANDE H.Damping loss factor estimation for coupled plates using experimental transient statistical energy analysis[C].52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference,Denver,United states,2011:1-7.

[3]PEREIRA R,ARENAS J P,ZUMELZU E.Comparison of four test methods to measure damping properties of materials by using piezoelectric transducers[J].Materials and Design,2011,32(4):2423-2428.

[4]姚德源，王其政.统计能量分析原理及其应用[M].北京：北京理工大学出版社，1995.

[5]LYON R H,DEJONG R G.Theory and application of statistical energy analysis(Second Edition)[M].The MIT Press,Cambridge.1995.

[6]郭书祥,吕震宙.区间运算和静力区间有限元[J].应用数学和力学,2001,22(12):1249-1254.

[7]DEGRAUWE D,LOMBAERT G,DE ROECK G.Improving interval analysis in finite element calculations by meansofaffine arithmetic[J].Computersand Structures,2010,88(3-4):247-254.

[8]张红亮.统计能量分析参数辨识及模型修正方法研究[D].哈尔滨：哈尔滨工业大学，2013.