一种电容器底部隔声腔尺寸优化方法

周 峰，匡 兵，刘夫云，李德玺，林 瑞

（桂林电子科技大学 机电工程学院，广西 桂林 541000）

随着人口的增多以及用地量越来越少，换流站常常建立在靠近居民的区域。因此，在高直流输电过程中，换流站中的电容器装置所辐射出来的噪声对周边的居民生活和健康都会产生不利的影响[1–4]。对单个电容器进行降噪是整个换流站中的电容器装置降噪的基础。所以，有必要对电容器的降噪措施进行研究，减少换流站噪声对周边居民的影响。

国内学者对于电容器降噪技术的研究已经取得一定的成果。吴鹏等提出用双底面结构来降低电容器底面的噪声，并在消声室进行实验，实验结果表明：具有双底面结构的电容器取得良好的降噪效果，降噪量约为10 dB[5]。袁剑等提出采用新型的复合降噪材料措施来降低电容器噪声，其仿真结果表明：吸声结构的降噪量可以达到达6 dB[6]。黄国兴等设计了复合微穿孔板吸声结构的电容器，实验结论:电容器底部和顶部的噪声量降低了6 dB～7 dB[7]。甘林等设计了一种波纹管减振器，实验表明：电容器底面方向降噪量达到9 dB[8]。上述降噪研究能够有效地降低电容器噪声，但考虑到电容器产品需要具有20年以上正常工作时间的特点，电容器生产企业采用的方法是在电容器底部增加隔声腔来降低噪声。采用在电容器底部增加隔声腔的方法进行降噪时，需要通过实验测试的方法来确定隔声腔的结构参数。这种实验测试方法不仅消耗大量的人力物力，而且会带来电容器产品周期难以控制的问题。因此，亟需对电容器底部隔声腔正向设计与优化方法开展研究。

为了提高电容器底部隔声腔的设计效率和质量，本文对电容器底部隔声腔尺寸优化方法进行研究。首先进行电容器隔声腔原理和设计理论分析，通过电容器噪声实验确定其底部噪声的主要贡献频率，并建立隔声腔有限元模型。然后，基于LMS Virtual Lab Optimization模块对隔声腔结构参数进行优化。设计噪声对比实验，验证模型的准确性和方法的正确性。

1 电容器底部隔声腔隔声机理分析

1.1 电容器底部隔声腔的隔声原理

如图1所示，从电容器内部传递出来的声波，一部分声能Er1被反射，另一部分声能Ei1引起隔声腔第一块钢板振动，并对隔声腔中的空气层辐射噪声。

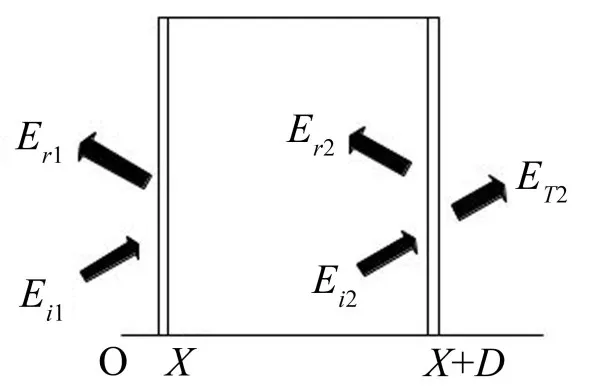
图1 声能在隔声腔中的传递

由于空气层具有弹性、减振的作用，部分声能得到损失，当空气声碰到第二块钢板时，一部分声能Er2声能被反射掉，而还有一部分Ei2要继续激起隔声腔第二块钢板的振动，向着隔声腔第二块钢板外辐射声音ET2，由于两块钢板的不连续性，使得声音得到降低[9]。我们可以把电容器底部隔声腔等效成为一个“质量-弹簧-质量”振动模型。

1.2 电容器底部隔声腔设计理论

目前电容器厂使用的电容器都是单底面结构，推导出从内部油到外部空气的电容器底部声压透射系数tp1为[10]

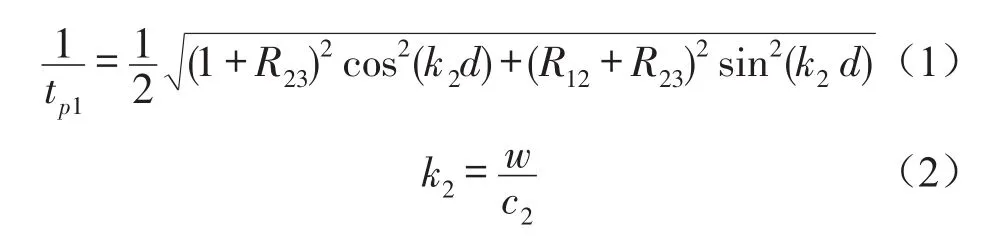
式中R12为电容器内部绝缘油的声阻抗与外壳声阻抗的比值；R23为外壳声阻抗与空气声阻抗之间的比值；d为电容器底面厚度；w为噪声角频率；c2为电容器底面外壳中的声速。

推导出电容器底部隔声腔声压透射系数tp2表达式为[11–12]

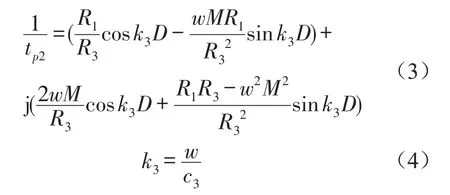
式中M为壳体的单位面积质量；R1为电容器内部绝缘油的声阻抗；R2为电容器外壳底面的声阻抗；R3为空气的声阻抗；D为电容器底部隔声腔中空气层的厚度；c3为空气中的声速。

电容器单底面和电容器底部隔声腔的隔声量L可以表示为

根据某电容器生产企业实际加工的电容器产品可知，电容器壳体厚度为2 mm，隔声腔中空气层厚度为24 mm，电容器油的声阻抗为1.5×106，电容器底面声阻为4.5×107，空气声阻抗为428.5，空气中的声速为340 m/s。根据式（1）至式（5）求解得到：电容器单底面的隔声量为32.44 dB，而电容器底部隔声腔的隔声量为49.2 dB，如果仅仅是考虑声波透射的情况下，电容器底部隔声腔比电容器单底面隔声效果增大了16.76 dB。

2 电容器底部隔声腔隔声仿真及优化分析

2.1 确定单台电容器底部噪声主要贡献频率

单台电容器底部噪声主要贡献频率一般是通过噪声测试得到的，图2为电容器振动与噪声测试方案图，施加的电流激励为：基频电流I1=45 A，谐波电流为I2=18 A、I5=8 A和I11=3 A。其中，测试设备为北京东方研究所开发的振动噪声测试与分析系统。在本次振动与噪声实验中，振动信号通道为2；同时噪声信号通道为5。将图2中两个类型的传感器采集得到的振动加速度和噪声声压时域信号导入DASP中进行分析，可以得到电容器底部噪声频谱图，如图3所示。

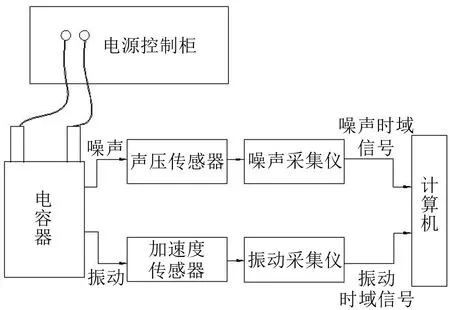
图2 电容器振动与噪声测试方案图

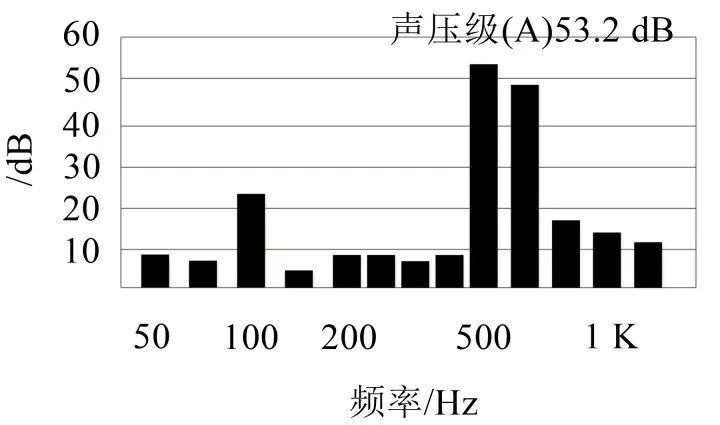
图3 电容器底部测点噪声A计权声压级频谱图

从图3可知，电容器底部测点噪声峰值集中在100 Hz、500 Hz、630 Hz、800 Hz和1 000 Hz，因此可知，单台电容器在正常工况下电容器底部辐射噪声贡献频率一般为100 Hz～1 000 Hz。

2.2 电容器底部隔声腔隔声仿真分析

2.2.1 电容器底部隔声腔有限元仿真模型

电容器底部隔声腔结构的材料属性如表1所示。电容器底部隔声腔主要由六块薄钢板和空气层组成。在有限元计算中，为了保证数值计算结果的准确性和精度，有必要对隔声腔有限元网格按照有限元划分要求进行划分，如表2所示，隔声腔结构网格和声学网格如图4所示。

表1 电容器底部隔声腔结构的材料属性

2.2.2 电容器底部隔声腔隔声量计算

表2 隔声腔网格划分要求

图4 隔声腔有限元网格

隔声量是指由于物体的阻碍作用，使得在金属片两边产生的声压衰减，金属片可以有一片、两片和多片组成。隔声量的计算通常用的是声音-固体耦合计算，因此，可以用耦合声学有限元计算封闭空间的隔声量[13]。本文在LMS Virtual Lab Acoustics中对隔声腔结构网格进行直接声振耦合计算，将仿真得到的隔声量与频率之间的特性曲线采用频谱修正。用1/3倍频程来评价隔声腔的隔声性能，与正常工况下电容器底部辐射噪声贡献频率保持一致，频带计算范围设为100 Hz～1 000 Hz，得到A计权隔声量，如图5所示。

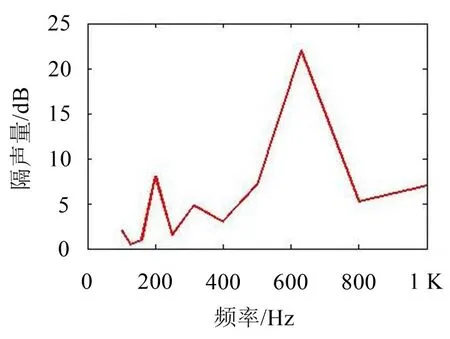
图5 电容器底部隔声腔隔声量与噪声频率之间的特性曲线

从图5可知，隔声腔在中高频的隔声量比低频范围的隔声量要高，并且隔声腔的隔声量在噪声贡献频率为630 Hz处有一个峰值。

2.3 电容器隔声腔尺寸D的优化分析

由式（3）可知，隔声腔尺寸D对于隔声量有较大的影响，因此，有必要对隔声腔尺寸D进行优化，找到一种满足工程应用要求的最优隔声腔尺寸。本文在2.2.2所建立的有限元模型基础上，将隔声腔有限元仿真模型导入到LMS Virtual Lab Optimization模块中进行优化分析，将隔声腔尺寸D作为其优化目标，利用DOE技术对其进行优化分析[13]，得到隔声腔尺寸D优化结果。

对隔声腔D进行优化时，选取的噪声频率范围应与2.1节所确定的电容器底部噪声贡献频率范围相同。下面对隔声腔尺寸D进行优化，选取隔声腔尺寸D和噪声频率f和面板质量M为设计变量，生成可接受的隔声腔直接声振耦合响应模型，并建立目标函数，优化问题的数学表达式为

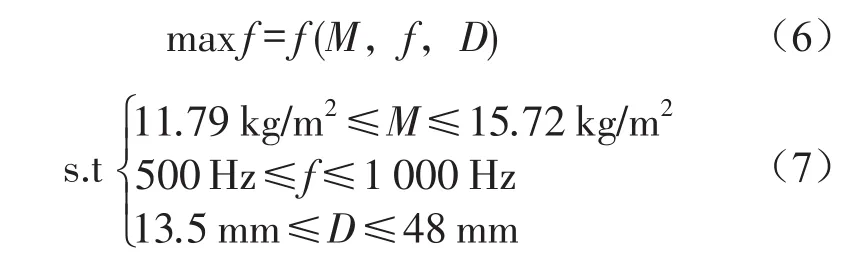
具体的隔声腔优化流程为：

(1)确定好隔声腔尺寸D、噪声频率f和面板质量M三个设计变量，采用间接法进行DOE分析；

(2)建立隔声腔直接声振耦合响应模型；

(3)建立目标函数，确定隔声腔尺寸D最优方案。

图6为优化目标函数曲线。从图中我们可以知道，当隔声腔尺寸D从13.5 mm至48 mm，曲线经历了增大-减小-增大的过程，最终在隔声腔尺寸D=23.5 mm时达到最优，此时隔声腔的隔声量从16.1 dB增大到23.6。通过对隔声腔尺寸D进行优化后，其隔声腔比其他同等型号电容器底面噪声降噪约7.5 dB。

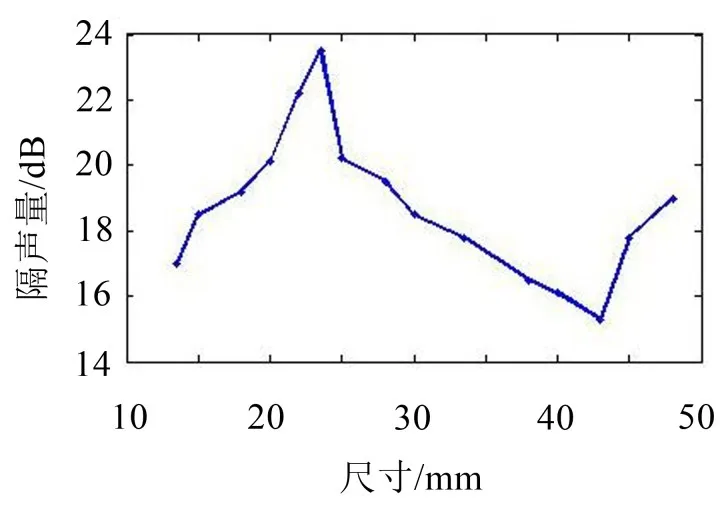
图6 优化目标函数曲线

3 电容器底部隔声腔噪声实验对比

3.1 电容器底部隔声腔隔声量测试

以某型号电容器为实验测试对象，其实际加工的底部隔声腔长宽尺寸为383 mm×197 mm，隔声腔尺寸D为35 mm，钢板厚度为2 mm，测试标准按照GB/T32524.1-2016进行。电容器噪声场点布置为：同时将五个声压传感器布置在距离电容器各面1 m左右，如图7所示。

图7 半消声室内实验设备布置图

在半消声室内施加电流激励，激励参数为基波I1=79 A，谐波为I5=1 A，I7=2 A，I11=31 A，I13=22 A，采用北京东方研究所开发的振动与噪声测试与分析系统进行测试，半消声室内背景噪声值为20 dB。

由于本文首先研究对象是电容器底部隔声腔隔声量与噪声频率之间的关系，所以先列出实测电容器底部隔声腔隔声量与噪声频率之间的特性曲线，如图8所示。

对比图5和图8可知，本文所建立的隔声腔有限元仿真模型的隔声腔隔声量与噪声频率之间的特性曲线与实测特性曲线变化趋势保持一致，而且均在630 Hz处达到隔声量峰值。具体对比值见下表3，仿真值与实测值均不超过2 dB，在允许的误差范围内，验证了仿真模型的准确性。

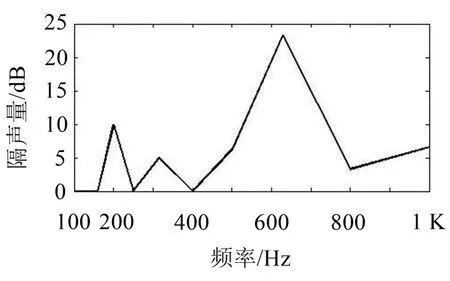
图8 实测电容器底部隔声腔隔声量与噪声频率之间的特性曲线

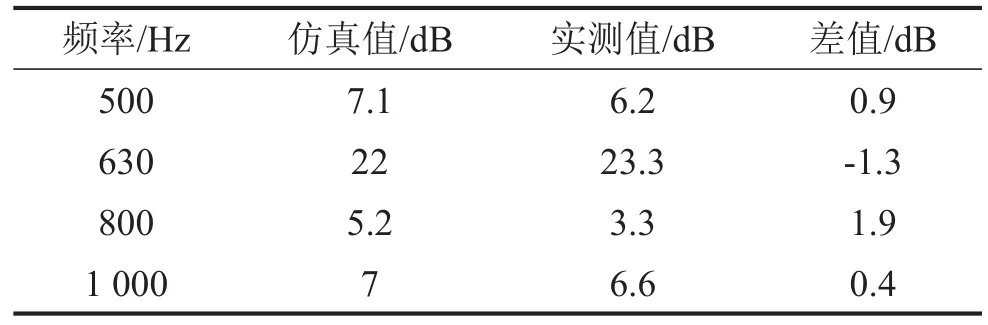
表 3电容器底部隔声腔隔声量仿真值与实测值对比

3.2 电容器底部隔声腔尺寸D测试

通过对隔声腔尺寸D进行隔声量测试，其底部隔声腔长宽尺寸为383 mm×197 mm，隔声腔尺寸D取值范围为13.5 mm～48 mm，钢板厚度为2 mm。实验条件同3.1节，实验分析得到实测隔声腔尺寸与隔声量之间特性曲线，如图9所示。

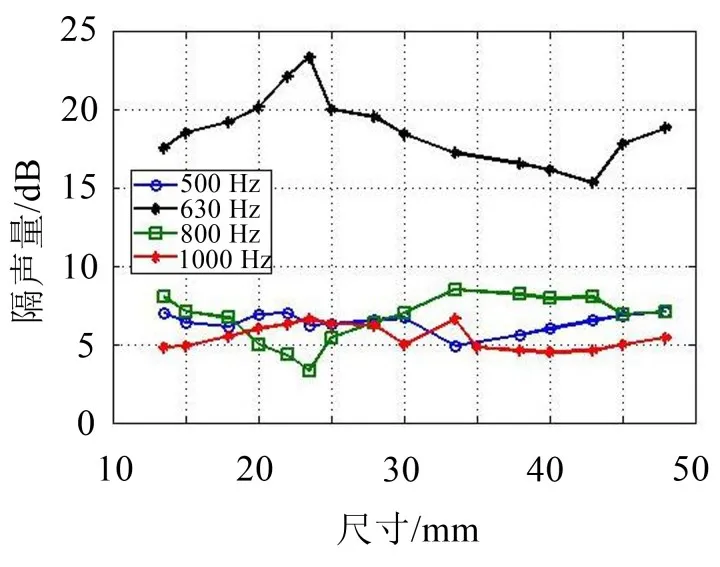
图9 实测隔声腔尺寸与隔声量之间的特性曲线

对比图6和图9可知，仿真优化和实测的隔声腔尺寸与隔声量特性曲线在噪声频率为630 Hz处变化趋势基本一致。仿真峰值与实测峰值均不超过1 dB，误差在允许的范围内，验证了本文提出的隔声腔优化方法的正确性。

4 结语

本文首先对电容器底部隔声腔隔声机理和设计理论进行分析；然后建立了隔声腔有限元仿真模型，并在LMS Virtual Lab Acoustics中使用直接有限元法对隔声腔进行隔声量计算；最后在LMS Virtual Lab Optimization模块中采用DOE技术对隔声腔尺寸D进行优化。可以得出以下结论：

（1）对电容器底部隔声腔有限元模型进行隔声量计算，其仿真结果与测试数据具有较高的吻合度，验证了模型的准确性。

（2）提出LMS Virtual Lab优化模块在产品设计中的应用，并通过优化设计得出了隔声腔的最优尺寸，与实验数据进行对比分析可知：优化后的隔声腔能够有效地降低电容器的辐射噪声，该应用对于隔声腔尺寸优化设计具有一定的参考价值。

[1]中国电力科学研究院.三峡—常州±500 kV直流输电工程可听噪声测试报告[R].2003.

[2]中国电力科学研究院.三峡—广州州±500 kV直流输电工程可听噪声测试报告[R].2004.

[3]河南电力试验研究所.灵宝换流站可听噪声测试报告[R].2003.

[4]CIGRE technical report.HVDC stations audible noise[R].No.202 W.G 14.26,France,2002.

[5]吴鹏，汲胜昌，曹涛，等.高压直流换流站交流滤波电容器降噪措施[J].电工技术学报，2011，26(1)：162-169.

[6]袁剑，钟永恒，田成，等.基于复合吸声结构的电容器降噪设计[J].科技创业月刊，2016，29(6)：112-113.

[7]黄国兴.电容器可听噪声分析与控制[D].合肥：合肥工业大学，2015.

[8]甘林.电容器噪声控制关键技术研究[D].桂林：桂林电子科技大学，2015.

[9]何琳.声学理论与工程应用[M].北京：科学出版社，2006.

[10]程建春.声学原理[M].北京：科学出版社，2012.

[11]BIES D H,HANSEN C H,CAMPBELL R H.Engineering Noise Control[M].Spon Press,2003.

[12]诺顿.工程噪声和振动分析基础[M].北京：航空工业出版社，1993.

[13]詹福良.Virtual.Lab Acoustics声学仿真计算从入门到精通[M].西安：西北工业大学出版社，2013.