飞机发动机变阻尼变刚度吊挂系统隔振性能的计算分析

闫鹏嗣，马建敏

（复旦大学 航空航天系，上海 200433）

高速运转的航空发动机是飞机飞行过程中的主要振源之一，如不加以隔离，其产生的剧烈振动会造成机体结构疲劳破坏和部分机载设备失灵，从而严重影响到飞机的飞行效能[1]；因此，发动机隔振问题一直受到广泛重视。

机翼下的吊挂结构是连接发动机和机翼的重要组成部分，起到传递推力和隔离振动的关键作用。刘亚奇等阐释了三种常见的翼下吊挂结构形式，并对其优缺点和适用范围进行了说明[2]。Depriest等提出传递率和性能比的概念，并详细介绍了发动机隔振安装的有效措施[3]。An Weigang等采用交互式多目标粒子群算法对吊挂结构进行优化设计，分析了载荷作用下吊挂质量和目标变量位移之间的对应关系[4]。Baklanov等考虑了发动机和机身的动柔度，提出了一种新的关于发动机振动辐射噪声的计算方法[5–6]。Iuspa等采用遗传算法对发动机吊挂系统的几何模型进行优化，获得了吊挂结构在满足发动机动力传递要求下的最小重量[7]。许飞等对发动机（安装节）-吊挂-机翼整体结构建立了有限元模型，分析了发动机安装结构的隔振特性[8]。宋波涛等建立了简化的吊挂结构模型，对比分析了不同工况下吊挂结构的隔振效果[9]。王会利等建立了由发动机和安装架组成的隔振系统力学模型，并利用有限元方法计算了该系统的隔振效率[10]。

发动机吊挂在发动机-吊挂-机翼系统中具有重要隔振作用，降低该系统的振动传递率往往需要降低其刚度，在具体应用时由于直接改变系统刚度难度较大，因此很多学者在研究该隔振系统时多将其刚度和阻尼视为固定不变的参数，很少从变阻尼变刚度的角度来研究和分析这一系统。本文为了对发动机吊挂系统的隔振性能进行全面深入的研究，分别在发动机安装节和吊挂连杆模型中添加了Voigt单元，调节Voigt单元中的可变阻尼能够改变安装节或连杆的刚度，构成两种不同的变阻尼变刚度发动机-吊挂-机翼系统，建立了其相应的力学模型和动力学方程；通过求解动力学方程，得到了系统振动传递率；通过计算分析调节安装节和连杆中的可变阻尼对系统振动传递率的影响，对比总结了两种变阻尼变刚度系统在相同频率范围内的不同隔振特征，以期对未来新型发动机吊挂系统的隔振设计提供理论参考依据。

1 变阻尼变刚度发动机-吊挂-机翼系统力学模型和动力学方程的建立

与以往将发动机安装节和吊挂连杆简化为固定参数的弹簧-阻尼模型不同，在建立发动机-吊挂-机翼系统时，分别在发动机安装节和吊挂连杆模型中添加Voigt单元，Voigt单元由刚度固定的弹簧和可变阻尼并联组成，调节Voigt单元中的可变阻尼能够改变安装节或连杆的刚度，安装节或连杆的阻尼受其中两个可变阻尼共同调节，构成两种不同的变阻尼变刚度系统。

1.1 发动机安装节模型中添加Voigt单元

在发动机安装节模型中添加Voigt单元后，建立的变阻尼变刚度发动机-吊挂-机翼系统力学模型如图1所示，称变阻尼变刚度系统1。

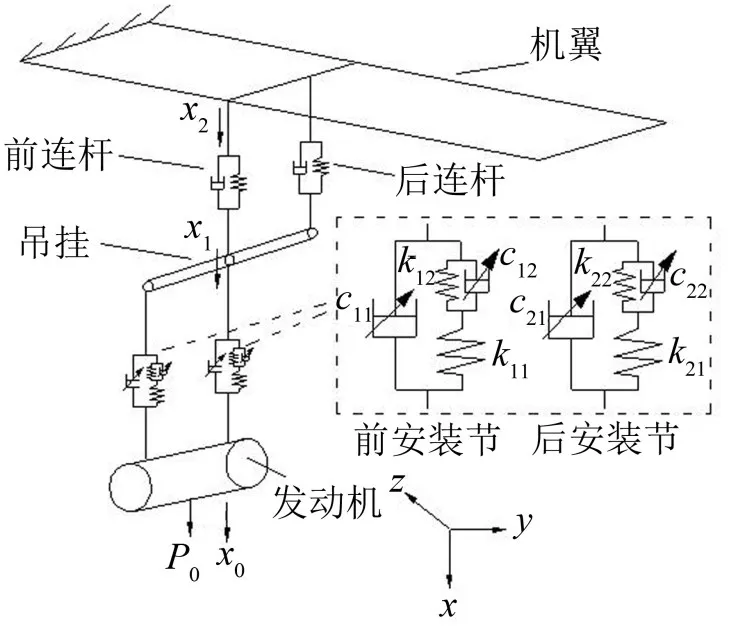
图1 变阻尼变刚度系统1力学模型

设发动机的振动位移为x0，质量m0集中于重心；吊挂和机翼前挂点在竖直方向上的绝对位移分别为x1和x2，其与发动机之间的相对位移分别为U1、U2；吊挂质量为m1，长度为2l，转动惯量为J，其质心位于几何中心，在发动机动载荷作用下绕质心转动,并有如下关系

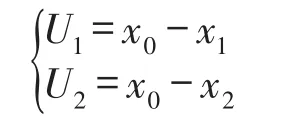
采用拉格朗日方程建立该系统的动力学方程，由各部件的动能、势能和耗散能可得到该系统的动力学方程，以矩阵形式表示

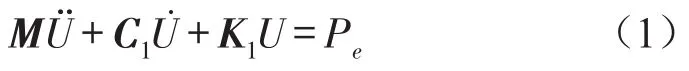
其中M为质量矩阵，C1为阻尼矩阵，K1为刚度矩阵

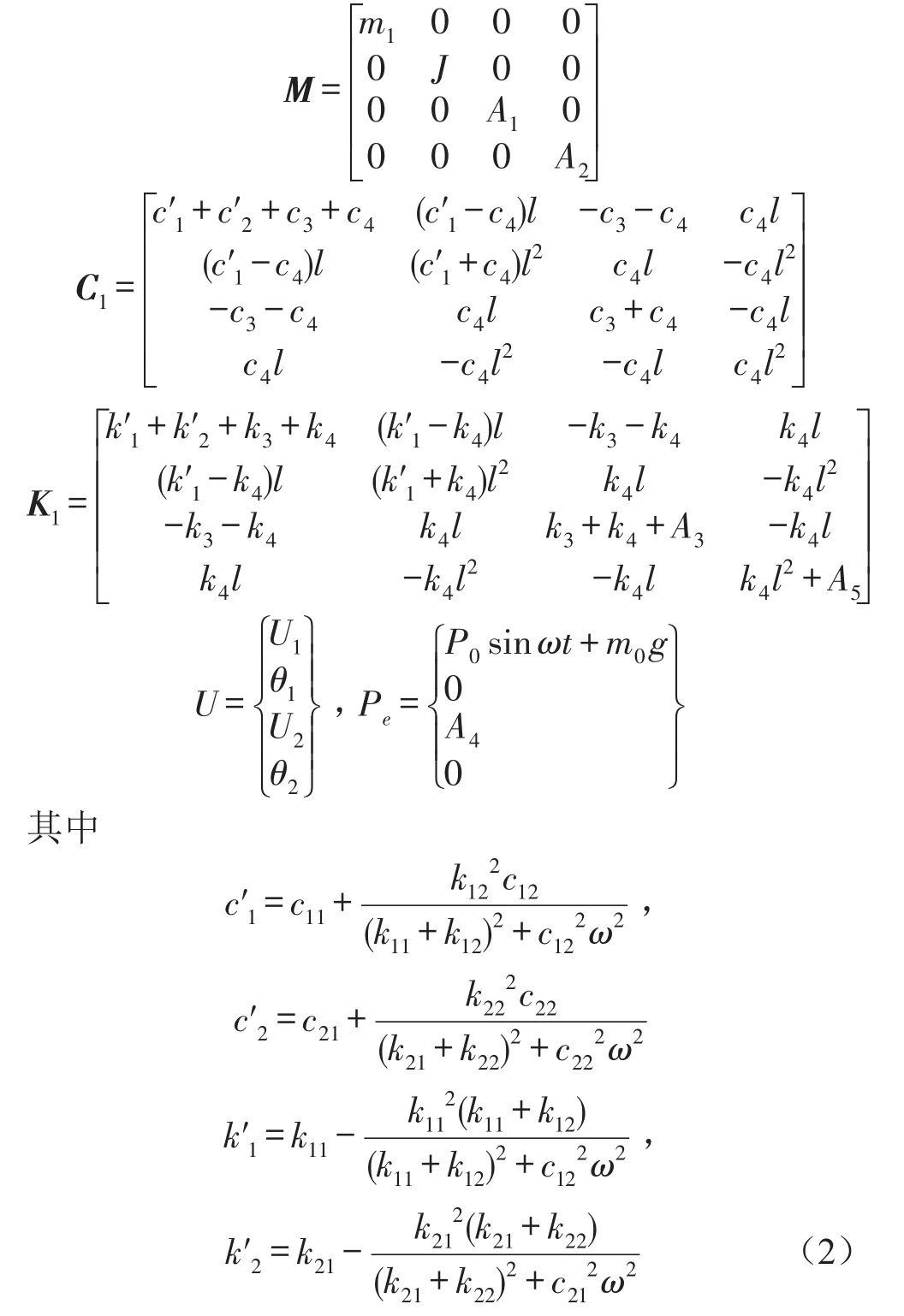
式中上角标“∙”、“∙∙”分别表示1阶和2阶导数；c11、c12和c21、c22分别为前后安装节中的两个可变阻尼系数，k11、k12和k21、k22分别为前后安装节中的2个弹簧刚度系数；c3、c4分别为前后连杆的阻尼系数，k3、k4分别为前后连杆的刚度系数；c′1、c′2和k′1、k′2分别为前后安装节的等效阻尼和等效刚度；

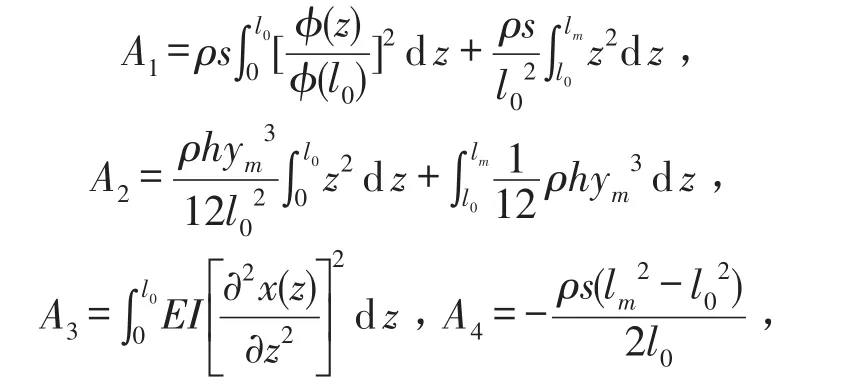
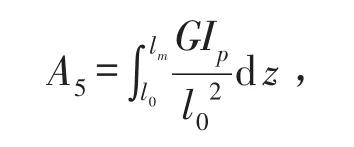
机翼弯曲振动仅考虑1阶振型，

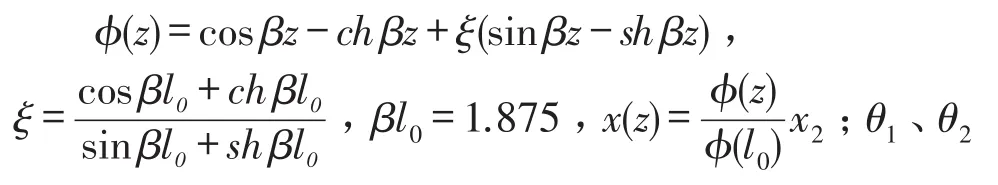
分别为吊挂和机翼的扭转角，lm、ym、h分别为机翼的长度、宽度和厚度，s为机翼横截面面积，ρ为其密度；z为沿翼展方向从翼根到机翼任一横截面的距离，l0为翼根到机翼挂点的距离，E为机翼弹性模量，G为机翼剪切模量，I为其截面惯性矩，Ip为机翼截面极惯性矩，P0sinωt为给发动机施加的简谐激振力。

1.2 吊挂连杆模型中添加Voigt单元

在吊挂连杆模型中添加Voigt单元，其力学模型与发动机安装节中添加Voigt单元的力学模型相同，只是模型中参数不同，建立的变阻尼变刚度发动机-吊挂-机翼系统如图2所示，称变阻尼变刚度系统2。

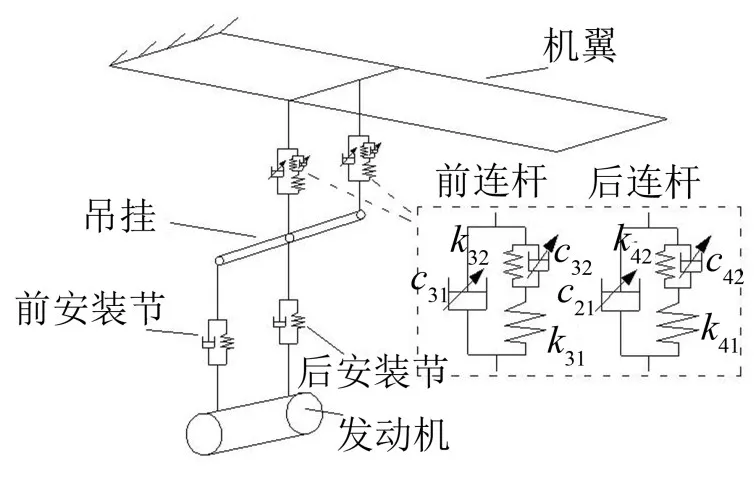
图2 变阻尼变刚度系统2力学模型

同样采用拉格朗日方程建立该系统的动力学方程，写成矩阵形式

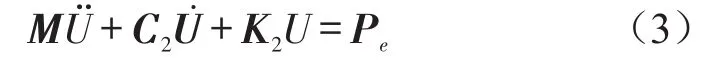
式（3）的矩阵M、U和Pe与式（1）相同，将阻尼阵C1中的c′1和c′2换成c1和c2、c3和c4换成c′3、c′4，便得到阻尼阵C2；同理，将刚度阵K1中的k′1和k′4，便得到刚度阵K2。其中

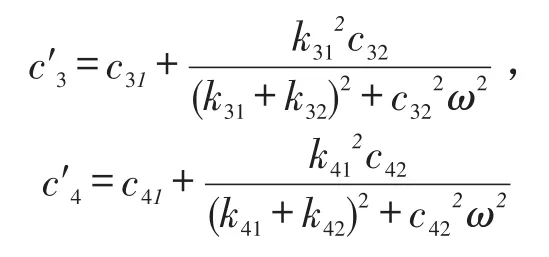
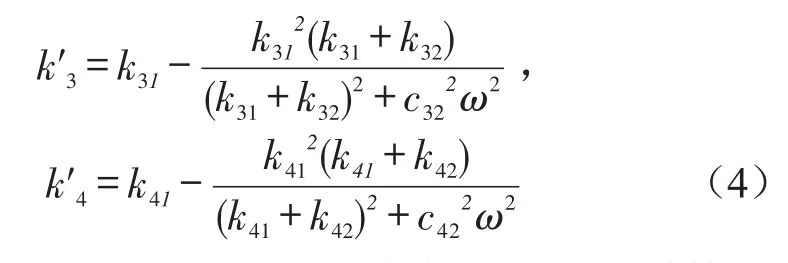
式中c1、c2和k1、k2分别前后安装节的阻尼系数和刚度系数；c31、c32和c41、c42分别为前后连杆中的两个可变阻尼系数，k31、k32和k41、k42分别为前后连杆中的两个弹簧刚度系数；c′3、c′4和k′3、k′4分别为前后连杆的等效阻尼和等效刚度，其余参数均与式（1）相同，不再重述。

2 变阻尼变刚度系统振动传递率的分析和讨论

2.1 变阻尼变刚度系统的振动传递率计算

将简谐激振力P0sinωt作用于发动机重心，分别将传递到机翼前挂点和后挂点的力幅值P1和P2与激振力P0之比定义为系统振动传递率TF1和TF2，即

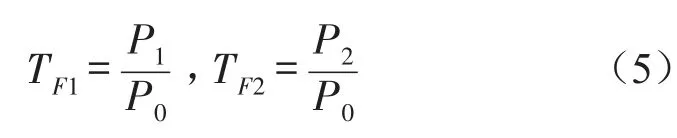
通过求解方程（1）和（3），可分别得到变阻尼变刚度系统1和2经机翼前后挂点计算的振动传递率。具体计算时取m0=2 000 kg，m1=450 kg，l=3 m，lm=14.2 m，l0=5.6 m，h=0.12 m，EI=3.21×108N∙m2，GIp=2.24×108N∙m2，k1=k2=1×106N/m，k3=k4=1×106N/m，kij=1×106N/m，i=1、2、3、4，j=1、2，P0=5 000 N，考虑到发动机的实际转速，激励频率ω取0～300 Hz。

为抑制系统可能产生的共振，计算变阻尼变刚度系统1和2的振动传递率时可变阻尼均取较大值，具体阻尼参数如表1所示。

将以上相应各参数分别代入式（1）和式（3），通过MATLAB编程计算，得到变阻尼变刚度系统1和2的振动传递率如图3和图4所示。

1）从图3可以看出，0～200 Hz范围内变阻尼变刚度系统1的前4阶共振峰分别对应系统前4阶固有频率ω1=14.3 Hz、ω2=50.9 Hz、ω3=95.3 Hz和ω4=139.1 Hz，与系统2相比，该系统的1阶共振峰得到显著抑制，但其他各阶共振峰均明显较高。经多次计算，发现增加安装节中的可变阻尼能有效抑制系统1的1阶共振，对其它各阶共振则没有明显的抑制效果。对于飞机发动机启动、停机必须经历的低频共振区，选取适当的安装节可变阻尼，可有效降低该系统的1阶共振峰值。

表1 0～300 Hz安装节和连杆的可变阻尼取值

2）与变阻尼变刚度系统1相比，0～200 Hz范围内变阻尼变刚度系统2的1阶共振峰值明显较高，而其它各阶共振峰却得到显著抑制，多次计算均发现增加连杆中的可变阻尼能显著抑制除系统1阶共振以外的其它各阶共振。具体应用时，可通过选取适当的连杆可变阻尼来抑制系统的高阶共振。

3）图4中200 Hz～300 Hz范围内，变阻尼变刚度系统1和2的振动传递率随着激励频率的增加而下降，系统1的振动传递率大于系统2。为了对比和分析调节可变阻尼对系统振动传递率的影响，下面计算可变阻尼取值减小时变阻尼变刚度系统1和2的振动传递率。

2.2 调节可变阻尼对系统振动传递率的影响

0～300 Hz范围内发动机安装节和吊挂连杆中的可变阻尼均取较小值，具体阻尼参数如表2所示。

将表中相应各参数分别代入式（1）和式（3），得到变阻尼变刚度系统1和2的振动传递率如图5和图6所示。

1）从图5可以看出，与图3相比0～200 Hz范围内变阻尼变刚度系统1的各阶共振峰均有升高，其中1阶共振峰值升高最为明显，即该频段内减小安装节中的可变阻尼会导致系统产生较高的1阶共振峰，使系统在低频区的隔振效果变得更差。

2）图5中0～200 Hz范围内变阻尼变刚度系统2的前4阶共振峰与图3相比也出现不同程度的升高，说明该频段内减小连杆中的可变阻尼会增加系统产生的各阶共振峰值，即不利于系统隔振。

3）图6中200 Hz～300 Hz范围内变阻尼变刚度系统1的振动传递率依然大于系统2，但与图4相比，系统1和2的振动传递率均得到了明显下降，即该频段内减小安装节或连杆中的可变阻尼会使系统的隔振效果得到进一步改善。

3 结语

分别在发动机安装节和吊挂连杆模型中添加Voig单元，从变阻尼变刚度的角度来研究和分析发动机-吊挂-机翼系统的振动传递率，通过对比和分析相同频率范围内可变阻尼在不同取值时对系统振动传递率的影响，可得到以下结论：

(1)0～200 Hz范围内可变阻尼取较大值时，发动机安装节中添加Voigt单元后系统的1阶共振得到了有效抑制，但对其它各阶共振抑制效果不明显；吊挂连杆中添加Voigt单元后系统的高阶共振得到了显著抑制，但对系统的1阶共振却没有明显的抑制效果；该频率范围内可变阻尼取较小值时，两变阻尼变刚度系统的前4阶共振峰均出现不同程度的升高，系统的隔振效果也变得更差。

表2 0～300 Hz安装节和连杆的可变阻尼取值

图3 0～200 Hz范围内系统振动传递率

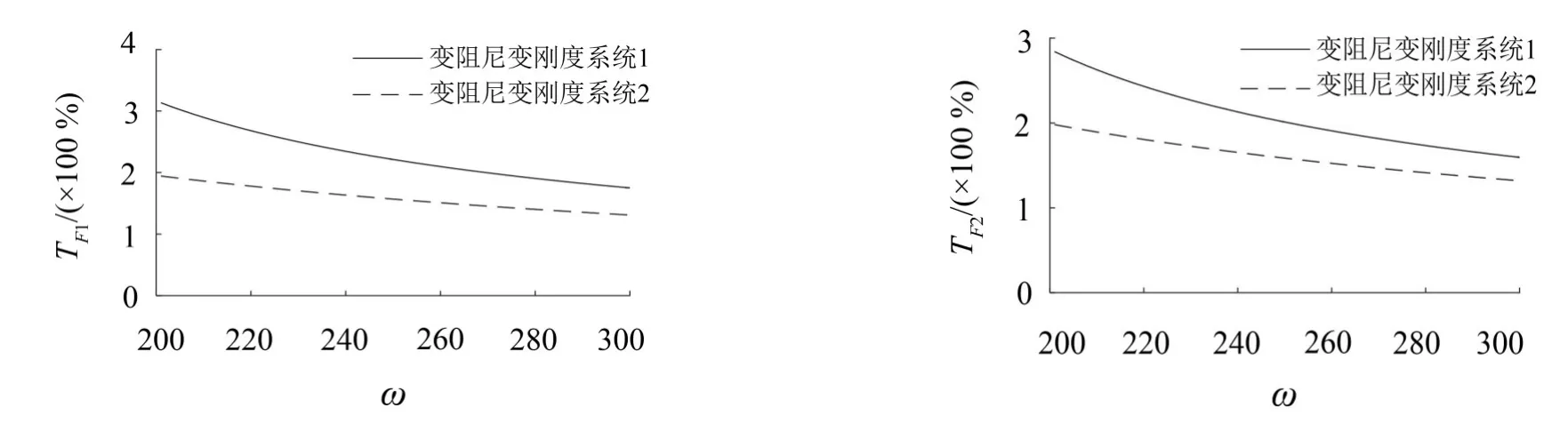
图4 200 Hz～300 Hz范围内系统振动传递率

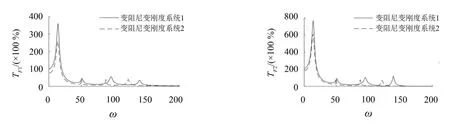
图5 0～200 Hz范围内降低可变阻尼后系统的振动传递率

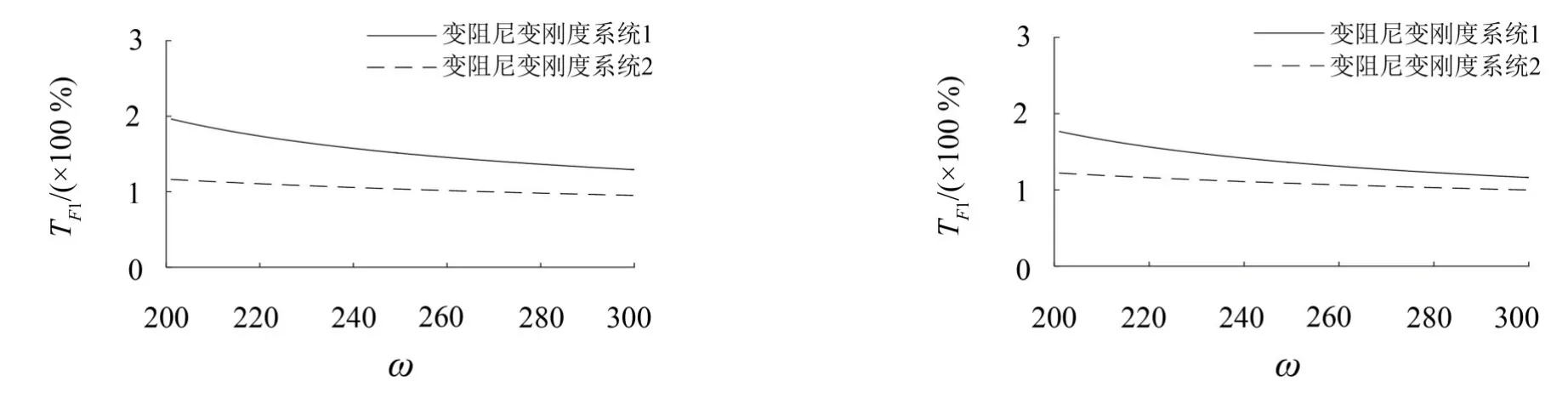
图6 200 Hz～300 Hz范围内降低可变阻尼后系统的振动传递率

(2)200 Hz～300 Hz范围内，可变阻尼取较大值时，两变阻尼变刚度系统的振动传递率较高；可变阻尼取较小值时，两变阻尼变刚度系统的振动传递率均明显下降，系统的隔振效果得到了进一步改善；该频段内与发动机安装节中添加Voigt单元相比，吊挂连杆中添加Voigt单元后系统的振动传递率始终较低，隔振效果也更好。

(3)根据本文的计算结果，今后加入主动或半主动控制，在0～200 Hz范围内自动调节安装节或连杆中的可变阻尼使其取较大值，以抑制系统产生的低阶或高阶共振；在200 Hz～300 Hz范围内自动调节安装节或连杆中的可变阻尼使其取较小值，可使系统的振动传递率得到进一步下降。在具体应用时，应根据系统的工作环境、激励频段和共振特征，选取适当的变阻尼变刚度吊挂系统结构形式，综合确定可变阻尼的取值，使变阻尼变刚度系统在不同频段均具有较好的隔振性能，这对未来新型发动机吊挂系统的研究和设计也有重要的参考价值。

[1]林国政.航空发动机的安装和振动控制[J].民用飞机设计与研究，2009(4)：44-47.

[2]刘亚奇，胡锦旋，刘星北，等.翼下发动机吊架及其与翼连接结构研究[J].民用飞机设计与研究，2009(S1)：74-76.

[3]DEPRIEST J.Aircraft engine attachment and vibration control[M].New York,NY,ETATS-UNIS:Society of Auto-motive Engineers,2000:11-19.

[4]WEIGANG AN,WEIJI L.Interactive Multi-objective Optimization Design for the Pylon Structure of an Airplane[J].Chinese Journal of Aeronautics,2007,20(6):524-528.

[5]BAKLANOV V S,ZAYAKIN A V.The calculation of structural noise in cabin for aircraft with high-by-pass ratio engines[C]//11 th AIAA/CEAS Aeroacoustics Conference(26 th AIAA Aeroacoustics,Conference).California:American,Institute of Aeronautics and Astronautics,2005,10.2514/6.2005-3034.

[6]BAKLANOV V S.Low-frequency vibroisolation mounting of power plants for new-generation airplanes with engines of extra-high bypass ratio[J].Journal of Sound and Vibration,2007(308):709-720.

[7]IUSPA L,SCARAMUZZINO F,PETRENGA P.Optimal design of an aircraft engine mount via bit-masking oriented genetic algorithms[J].Advances in Engineering Software,2003,34(11-12):707-720.

[8]许飞，贺尔铭，李景旭.翼吊发动机安装结构等效建模及其隔振设计[J].航空动力学报，2016(8)：1905-1912.

[9]宋波涛，贺尔铭，张钊，等.翼吊发动机吊架结构等效建模及隔振特性分析[J].科学技术与工程，2012，12(4)：832-836.

[10]王会利，苏尔敦.某型飞机发动机隔振系统设计与振动特性分析[J].装备环境工程，2015（6）：121-126.