基于预实验分析的箱梁模型模态测试

曾少辉，雷晓燕，罗 锟，汪振国，欧开宽

(1.华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013；2.南昌华路建设咨询监理有限公司，南昌 330013)

在对结构进行模态识别时，测点位置布置的恰当与否直接影响着最终的识别结果。而模态识别的基本思路是利用有限个自由度（即测点数量）去描述无限自由度结构尽可能多的模态，因此传感器位置的布置必须准确、合理以保证识别数据的有效性。

以往人们在制定测点布置方案时，大多根据经验来确定。但随着时代的发展，人们意识到仅凭经验确定的布点方案往往存在一定的缺陷，有时可能需要多次实验结果进行验证及修改，才可能得到较准确的结果。因此，人们开始对布点方法进行研究并提出许多方法用于确定测点位置。李兆霞等提出通过建立结构的有限元模型分析结构的动力特性，并根据得到的振型初步确定测点的方法来确定布点方案[1]。Kammer在对大型空间结构进行模态识别时，运用了一种有效独立法确定测点位置[2–4]。李戈等在对香港青马悬索桥健康监测中，分别采用广义遗传算法及经典遗传算法寻找最优测点，结果显示广义遗传算法不仅结果稳定且收敛速度快[5]。刘斌等在对斜拉桥的监测当中，分别运用了有效独立法及MAC法进行布点研究，并探讨了振型阶数对测点布置的影响[6]。戴航等提出了一种基于多种算法的混合算法：利用MAC法确定初始测点，有效独立法确定候选添加点确定最终布点，并以实验梁为研究对象对该方法进行了应用，且将结果与其他方法进行了比较[7]。

以上方法虽然确定了最优测点，但没有相应的方法确定激励点位置。而在模态试验中，大多需要对结构施加激励，而激励位置的确定也是十分关键的，它决定着所施加的激励能否激起所关心的模态。本文以箱梁模型为例，运用预实验分析[8]方法确定最优布点方案及最优激励点位置，以此对箱梁模型进行模态识别。

本文思路是先建立箱梁模型的有限元模型进行模态分析，得到箱梁模型的振动特性，根据所得模态分析结果初步确定布点位置；再由预实验分析对布点位置进行MAC验证，评价布点位置的合理性，确定最优布点；并运用预实验分析确定最优激励点位置；接着，按照预实验分析结果进行模态试验；最后，将实验模态与有限元模态进行相关性分析验证实验结果的正确性。图1为预实验分析流程。

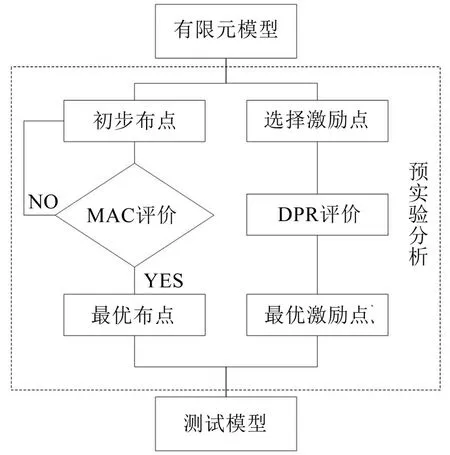
图1 预实验分析流程图

1 箱梁模型预实验分析

本文模态识别的对象为高架箱梁10:1缩尺模型，模型桥长3.2 m，顶板宽1.2 m，底板宽0.55 m，高0.305 m。模型浇筑材料为灌浆料，模型材料的弹性模量为：30 Gpa，密度为2 203.7 kg/m3。

该模型是用于研究高架箱梁振动特性所浇筑的缩尺模型，最终目的是利用在缩尺模型得到的实验结果反演至原型，以此来研究高架箱梁的振动特性。为保证模型试验顺利进行，必须要确保所制作的缩尺模型的正确性。通过识别缩尺模型的模态与有限元分析结果对比，以验证模型与原型之间的相关性。本文的内容主要以缩尺模型模态识别为主。

1.1 箱梁模型有限元模态分析

箱梁模型有限元模型采用实体单元进行模拟，并将灌浆料参数代入模型。箱梁模型有限元模型是处在自由边界条件下，进行自由模态分析，分析共提取箱梁模型前5阶模态（为去除前6阶刚体模态后的前5阶），分析结果见表1。

表1 箱梁模型有限元模态

可以看到箱梁模型的自由模态前5阶固有频率都在300 Hz以内，包含2阶竖弯，2阶扭转及1阶侧扭。

1.2 预实验分析原理

1.2.1 测点布置位置评价

有限元模态分析结果中可以得到所关心阶数的数据，因而在有限元模型上进行布点，所布测点相应地包含各阶模态数据。而模态实验最终是利用所选的测点描述所要识别的各阶模态，为避免所选的测点过少使得模态识别结果产生混淆，需要对这些测点进行评价。预实验分析利用所选测点包含的有限元模态数据进行模态置信度验证（MAC），通过得到的MAC矩阵对布点方案评价。通常认为理想的布点方案得到的MAC矩阵中，对角线值应为1，非对角线值则应尽可能的小。式（1）为MAC计算公式

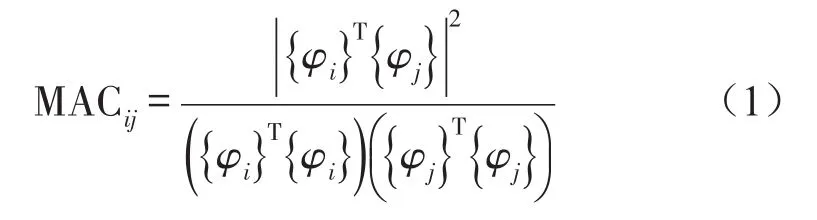
其中{φi}表示第i阶模态向量；{φj}表示第j阶模态向量。

1.2.2 激励点位置评价

对于激振器法模态试验中，理想激励点应满足在该点施加激励时，能将所关心的模态完全激起。但对于如何确定这样一个理想的激励点，一直很少有合理且有效的方法进行确定。预实验分析中，提供了一种驱动点残差值[8]（DPR）对各候选激励点进行评价的方法确定最理想的激励点。其原理是通过计算各激励点在各阶模态振型下的原点传函，每阶振型响应的原点传函值，由其值的大小来确定各激励点的优劣。DPR计算公式如下

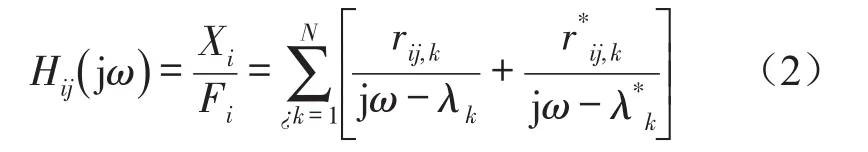
其中Hij(jω)表示在j点激励i点的频响函数；rij,k表示第k阶模态的留数；λk表示第k阶模态的极点；*表示共轭。

其中极点值，λk=δk+jωdk，

ωdk表示有阻尼时的第k阶模态频率值，ωnk表示无阻尼时的第k阶模态频率值，δk表示第k阶模态的阻尼因子，ζk表示第k阶模态的阻尼比。

第k阶模态的留数rij,k=υikυjk，ak为换算系数，

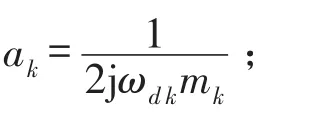
υik表示第k阶模态响应点i点的模态形状系数；υjk表示第k阶模态激励点j点的模态形状系数。

1.3 箱梁模型预实验分析

图2（a）为预实验分析确定的测点布置位置，每截面布置8个测点，沿桥纵线方向每0.4 m布置一截面，布置9个截面共72个测点；图2（b）为初步选定的7个激励点。

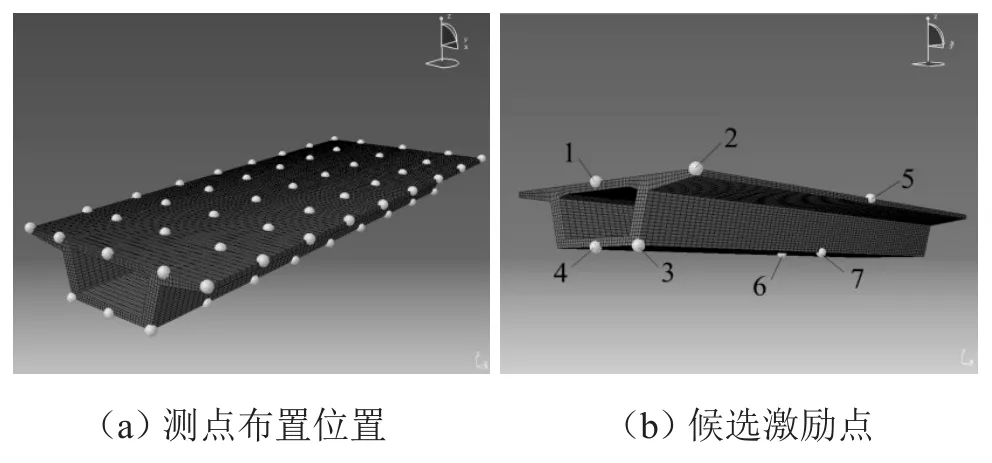
图2 测点及激励点位置示意图

图3为预实验分析对测点位置做出的MAC评价，图中对角线的值都为1，而非对角线的值都为0。说明该布点方案，完全能够描述所需识别的5阶模态，且识别出的模态之间出现混淆的可能性也很低，即各阶模态之间具有较高的独立性。

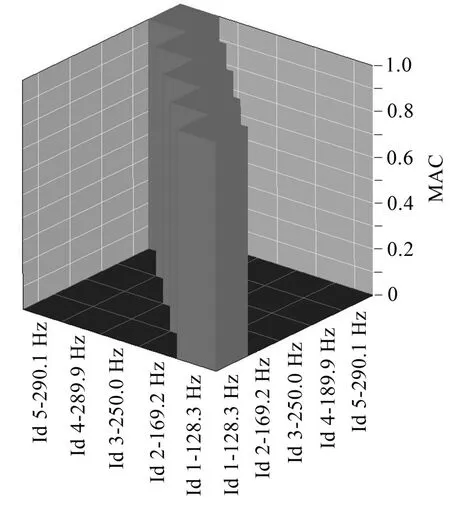
图3 测点MAC矩阵

图4为候选激励点各个方向的DPR值，考虑到试验时，其中有些测点的某些方向无法进行激励，图4仅列出能实现激励的候选点方向的DPR值。

图中还列出各点各方向DPR值的最小值、最大值、平均值及加权平均值。候选激励点2的+Z方向的DPR值不论是平均值或是加权平均值都远大于其余各点，说明2号点+Z方向的激励是最优的，由此确定其为实验激励点。

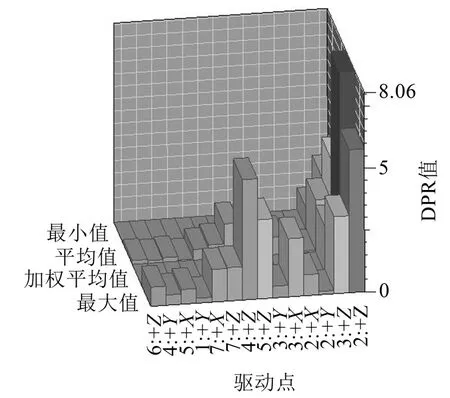
图4 各候选激励点各方向DPR值

2 箱梁模型模态测试

2.1 箱梁模型模态测试

试验概况：支撑方式：使用起重吊带穿过浇筑时在模型顶板预埋的构件将箱梁模型悬挂，以使箱梁模型处于自由支撑状态，见图5。

图5 箱梁模型支撑状态

激励位置及信号：由预实验分析结果可知2号点+Z向激励最优，实验时，按照预实验分析结果在翼缘板顶端部位垂向施加激励，见图6。

图6 激励点位置

由于猝发随机信号既有周期性，同时又具有随机性，而且还具备瞬态性，使得测试速度加快，实验过程中为提高实验效率采用猝发随机信号作为激励信号进行实验，激励频带宽为：0～1 024 Hz。

实验设备：加速度传感器：PCB 356A16三向加速度传感器；力传感器：PCB 208C02；数采仪器：比利时LMS公司310数据采集系统；分析软件：LMS TEST.Lab软件，MIMO FRF Testing模块。

考虑到传感器数量的不足，分批次进行采集，每次采集4个测点。在数据采集过程为保证获得频响函数的质量，应使在所关心的频率范围内相干函数的值大于0.8。本次试验采集的相干函数数据显示，在测试频率范围内相干函数值基本保持在0.8以上，尤其在分析频率段：120 Hz～300 Hz范围内其平均值达到0.88以上。由此测得的频响函数进行分析得出的稳态图也能清晰地识别各阶模态参数。

2.2 模态测试结果分析及对比

通过测量得到频响函数，进行模态参数识别，采用Poly MAX方法进行拟合识别各阶模态参数。预实验分析时识别目标为箱梁模型的前5阶模态，在进行参数识别时，将分析范围设置为120 Hz～300 Hz。此次试验共识别出4阶模态，分别对应有限元模态的第1、2、3、5阶模态。图7为识别的4阶模态MAC矩阵图，可以看到在对角线其值都为1，而在非对角线最大值不超过0.2，说明所识别的模态之间的独立性较好。

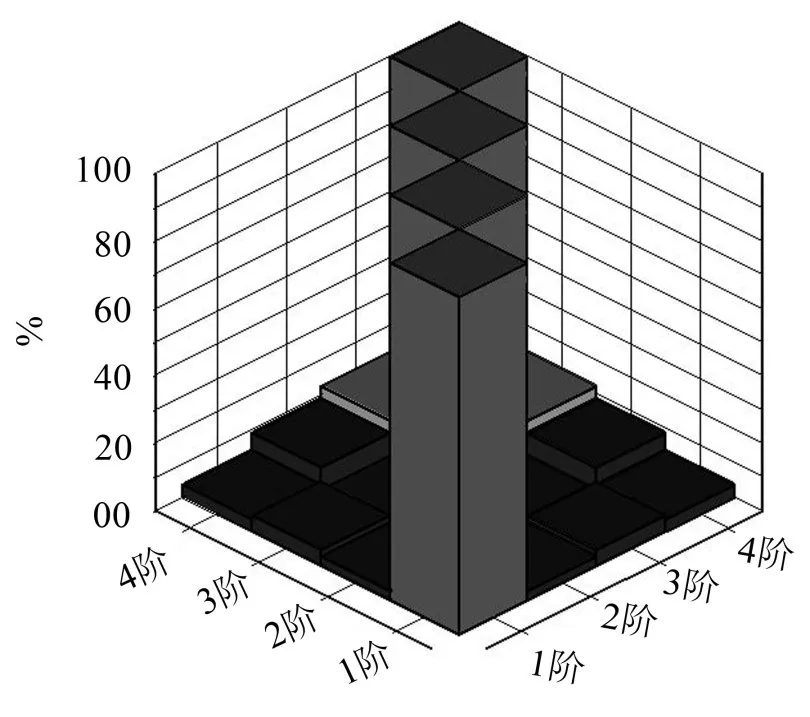
图7 实验模态MAC矩阵

图8为模态测试所识别的4阶模态振型图，从振型图可看到识别出的振型与有限元分析得到的振型基本相似，特别是前2阶。

表2列出了本次模态识别的结果，共识别出4阶模态，有限元模态的第4阶模态未识别出，从其振型可以看出该阶模态振型表现出较明显的横向扭转，因此，要识别出该阶模态需要施加横向激励。从整体来看，识别率还是比较高的。从实验模态与有限元模态频率值的误差来看，前3阶的误差都在5%以内，第5阶误差较大为8.083%。

图8 识别模态振型

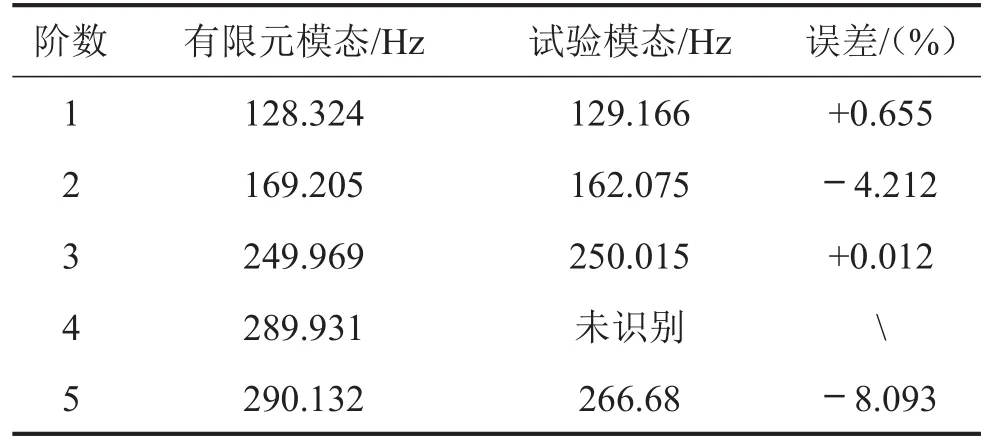
表2 模态识别结果

为进一步确定有限元模态振型与试验模态振型之间的相关性，对两者的振型进行相关性分析，分析结果见图9。

识别的4阶模态与对应的有限元模态的MAC值分别为：0.927、0.944、0.691、0.709。在实际工程中，通常认为MAC＞0.7的2阶模态相似程度好，而MAC＜0.5说明2阶模态相似程度差。从此次模态试验识别结果来看，识别的模态与有限元分析结果吻合程度较高，说明实验模态数据的正确性，同时也表明预实验分析的有效性。

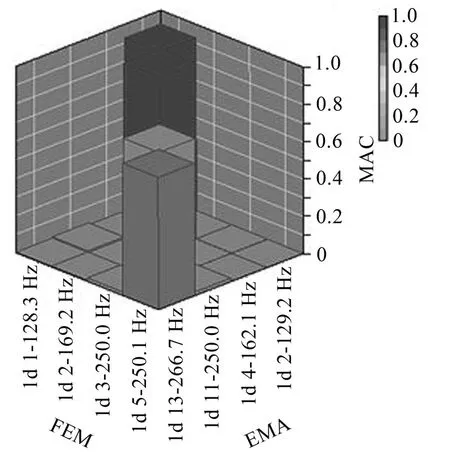
图9 有限元模态与实验模态MAC图

3 结语

本文采用激振器法对箱梁模型进行模态识别，识别过程中通过使用预实验分析对测点布置位置进行评价确定最终测试测点的布置，再由DPR值确定最优激励点。最后将实验模态与有限元模态进行对比，得到如下结论：

（1）使用预实验分析对测点方案进行评价，不仅能使识别效果大大提高，且能防止模态混淆；

（2）使用预实验分析确定的最优激励点进行实验，模态识别率较高；

（3）实验模态与有限元模态之间的相关性分析可以确定两者相关程度，确保实验模态的正确性。

[1]李兆霞，李爱群，陈鸿天，等.大跨度桥梁结构以健康监测和状态评估为目标的有限元模拟[J].东南大学学报(科学版)，2003，33（5）：562-572.

[2]KAMMER D C.Sensor placement for on-orbit modal identification and correlation of large space structures[J].Journal of Guidance Control Dynamics,1991,14(2):251-259.

[3]KAMMER D C.Effect of modal error on sensor placement for on- orbit modal identifiaction and correlation oflarge space structures[J].Journalof Guidance Control Dynamics,1992,15(2):334-341.

[4]KAMMER D C.Effect of noise on sensor placement for on- orbit modal identification and correlation of large space structures[J].JournalofGuidanceControl Dynamics,1992,15(2):341-352.

[5]李戈，秦权，董聪.用遗传算法选择悬索桥监测系统中传感器的最优布点[J].工程力学，2000(1)：25-34.

[6]刘斌，姚永丁，叶贵如.斜拉桥传感器优化布点研究[J].工程力学，2005(5)：171-176.

[7]戴航，袁爱民.基于灵敏度分析的结构模型修正[M].北京：科学出版社，2011.

[8]LMS Virtul.Lab 7ASoftware Manual．