高层建筑简化振型及在结构风振计算中的应用

王国砚， 张福寿

(同济大学 航空航天与力学学院， 上海 200092)

风荷载是高层建筑的主要水平荷载之一.目前，工程上普遍采用基于振型分解法的随机振动理论计算风振系数[1]，由此确定风荷载，并据此进行结构风振响应计算.可见，振型在整个结构风振计算中扮演着重要的角色，尤其是平动基阶振型.然而，实际结构的振型复杂多变，难以直接应用于结构风振计算.各国在编制风荷载规范时，往往采用弯剪型悬臂梁模型来模拟等截面匀质高层建筑，并据此建立高层建筑振型的计算式.即使这样，得出的振型表达式仍十分复杂.因此，仍需要对高层建筑振型做进一步的简化.简化振型的表达式能否准确反映高层建筑的实际基阶振型，是在设计阶段预估响应的一个重要环节[2].

在早期，为计算简便，通常将高层建筑基阶振型简化为如式(1)所示的线性振型[3]:

φ1=z/H

(1)

式中:φ1为归一化振型；H为建筑总高；z为各楼层高度.在风洞实验中，利用高频动态天平直接测量模型的基底弯矩来获得广义气动力时也是基于这一假定[3].Vickery分析了当简化的直线振型偏离建筑物的实际振型时所造成的误差[3].Holmes、周印等[4-6]对线性振型进一步做出修正，给出幂函数形式的简化振型如下：

φ1=(z/H)β

(2)

其中，β为控制振型形状的量纲一参数，并分别给出对应于结构风致响应计算的不同修正方案.目前，美国风荷载规范[7]依旧沿用式(1)给出的线性振型；欧洲规范[8]则采用式(2)，其β值按照结构类型来划分；日本规范[9]也采用式(2)，并根据结构实际振动模态与参考模态的一致性和结构质量分布特征取修正系数φD[10].

我国风荷载规范[11]则是给出了两类简化振型.一类是考虑结构弯剪变形特点的正切函数形式:

(3)

另一类是基于框剪协同工作原理针对框架剪力墙结构给出的当弯剪均起主要作用的振型，如荷载规范[11]中表G.0.3所示.梁枢果[2]经过对大量高层建筑振型曲线的观察和总结，发现现有的高层建筑平动一阶振型大部分是上剪下弯的弯剪型，与规范[11]中上弯下剪的正切形式有很大差异，认为采用如下的简化振型：

(4)

较符合.徐永林等[12]对金茂大厦进行实测，得到其基阶振型,认为此振型用式(2)拟合更为贴切，并指出不同建筑结构体系的振型形态各不相同，应在荷载规范中对此进行分类.李永贵等[13]分析了因简化振型的不同对风振计算结果的影响,认为：当结构振型与规范振型式(3)相差较大时，若仍采用规范振型计算，风致基底剪力偏差可达5%以上.

可见，各文献给出的简化振型都存在差异，依据不同简化振型求得的风致响应也存在较大偏差，而且目前对振型形状控制参数的研究也很少见.因此，本文对简化振型做进一步改进，给出能更准确反映高层建筑实际振型的简化振型，从而提高风荷载和风振响应计算的精度.

1 基于弯剪梁模型的高层建筑理论振型

对高层建筑风荷载分析时，一般将其简化为一维竖向悬臂梁结构.对于质量和刚度沿高度比较均匀的高层建筑,考虑整体剪切变形影响 ,对应梁模型的自由振动微分方程为[1]

(5)

式中:y为梁横向挠度；EI为弯剪梁的弯曲刚度；GA为剪切刚度；m为单位梁长质量；χ为考虑切应力沿截面分布不均匀而引入的修正系数，简称剪切系数.对于不同形状的截面，剪切系数χ可按文献[14]中给出的相关公式计算；其中，矩形截面可取5/6，圆形截面可取9/10.

求解方程(5)，结合悬臂结构边界条件，可解得频率方程[1]如下：

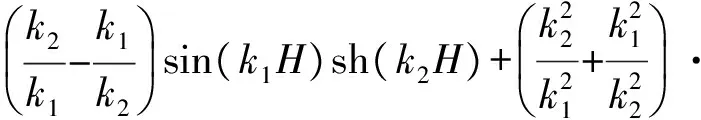
cos(k1H)ch(k2H)=0

(6)

以及振型函数：

(cos(k1z)-ch(k1z))

(7)

式中:k1，k2为参数.且

(8)

令

(9)

H为梁长,则由式(6)可得弯剪梁的频率为

(10)

由式(8)和(9)可得:

(11)

令X=z/H，并对振型作如下归一化:

φ1(X)=φ(z)/φ(H)=φ(XH)/φ(H)

(12)

将k1H、k2H分别看成整体，当λ确定时，联立式(6)和(11)即可解出k1H、k2H.k1H、k2H有无穷多组解，每一组解对应每一阶固有频率和振型.将第一组解(k11H、k21H)代入式(12)即可得到对应的归一化基阶振型.在整个求解过程中，一旦λ确定，后续求解振型φ1(x)就不再与高度、质量密度、刚度、剪切系数χ等结构参数有关.因此，控制任意等截面匀质弯剪梁振型形状的影响参数可归结为λ这一结构特征参数，这给弯剪梁的振型分析带来很大便利.

从式(9)看出，λ反映的是结构的变形特征，为量纲一参数.λ值越小，结构越呈剪切变形特征；λ值越大，结构越呈弯曲变形特征.本文参照文献[1]，取16个λ值，求解得到与基阶振型对应的16个k11H值，如表1所示.

表1 结构特征参数λ与k11H之间的关系

进一步，由式(11)得到相应的k21H值，代入式(12)得到每个λ值对应的基阶振型，对应的振型曲线族如图1所示.

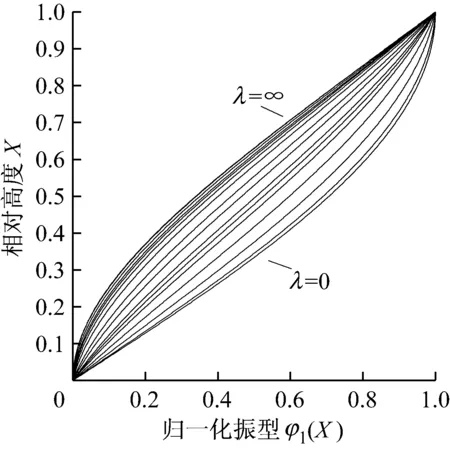
图1 弯剪梁基阶振型曲线族

可见，当λ取0时可退化为纯剪切梁，其基阶振型为图1中最下部的曲线.随着λ值增大，振型逐步向弯曲型过渡，在过渡区，基本呈现出上剪下弯的弯剪型变形特点.弯曲变形在振型中所占的优势随λ呈递增关系，当λ趋于无穷大时，可退化为纯弯曲梁，其基阶振型为图1中最上部的曲线.当λ的取值在30到无穷大区间时，基阶振型的变动幅度很小.

值得注意的是：本文的λ与框架剪力墙结构协同工作的刚度特征值λ[15]有所区别，本文λ体现的是建筑结构整体等效抗剪刚度与抗弯刚度的比值，是从结构整体性出发，适用于多种结构体系，而框剪协同工作的λ体现的是框架抗剪刚度与剪力墙抗弯刚度之间的比值，主要针对框架剪力墙结构.

由式(12)可得出高层建筑基阶振型的理论解.它的特点是，可理解为是在满足题设条件下的精确解，对具有任意形状对称截面(质心与刚心重合)的等截面高层建筑均适用；但计算表达式复杂，不便于工程应用.在实际工程应用中，往往选择既能满足精度要求又便于工程计算的实用简化振型.

2 基阶振型简化方案

2.1 本文提出的基阶振型简化模型

引言部分给出的式(1) ～ (4)为目前国内外常见的几种高层建筑基阶振型简化模型.在此，本文先选择其中的三个简化模型，即：

式中:X=z/H，振型的指数统一用β表示.通过非线性拟合，分析它们的振型曲线族与图1的曲线族之间的近似程度.以式(13)为例，将β作为待定参数，通过非线性最小二乘法对图1中16个λ值对应的16条振型曲线分别进行拟合，确定每一曲线的最优β值，从而得到图2a中近似的振型曲线族.每个λ确定的振型对应一个由简化振型拟合的参数β.再将拟合振型与图1的振型比较，如图2b所示，为便于观察，选取图1中λ1=∞、λ2=3、λ3=1.6、λ4=0对应的4个振型和与之对应的拟合振型进行比较.图2b中的4条线从上到下依次对应于λ1=∞、λ2=3、λ3=1.6、λ4=0的弯剪梁振型，β1～β4的4条曲线则依次是与之对应的拟合曲线；图2c～图2f也是如此.可看出，采用式(13)对弯曲型振型拟合效果较好，对偏剪的则误差较大而且体现不出下弯上剪的振型特点.同理，以式(14)、(15)为简化模型，进行拟合分析，并将所得简化振型与图1的振型比较，如图2c和图2d所示.可见，虽然它们都能体现弯剪型，但拟合效果也不是很好.

经此分析后发现，在这些简化模型的基础上，还有一定的改进空间.为此，本文从兼顾精确性与实用性出发，在式(13) ～ (15)基础上，通过变形、组合、退化处理后，得出以下两个简化振型表达式：

将由式(16)和式(17)给出的简化振型与图1比较，如图2e和图2f所示.可见，每一振型曲线都能一一吻合.这表明，本文给出的两个简化振型均能够达到很好的拟合效果.其中，式(17)给出的简化振型融合了式(13)和式(14)的优点，函数形式简单，对弯曲剪切都具有很好的吻合效果，也包含了上剪下弯的振型形式.因此，本文推荐采用该简化振型模拟高层建筑的基阶平动振型，式中的β定义为振型指数.

2.2 振型指数β的确定

由弯剪梁动力特性分析可知，每一个λ对应一条振型曲线，而采用简化振型对其拟合时也有相应的一个待定系数值β，λ与β之间存在一定的映射关系.表2给出了振型简化式(17)中振型指数β与λ对应关系，二者的关系曲线如图3中实线所示.

a 由式(13)拟合的振型曲线族

b 式(13)的拟合效果

c 式(14)的拟合效果

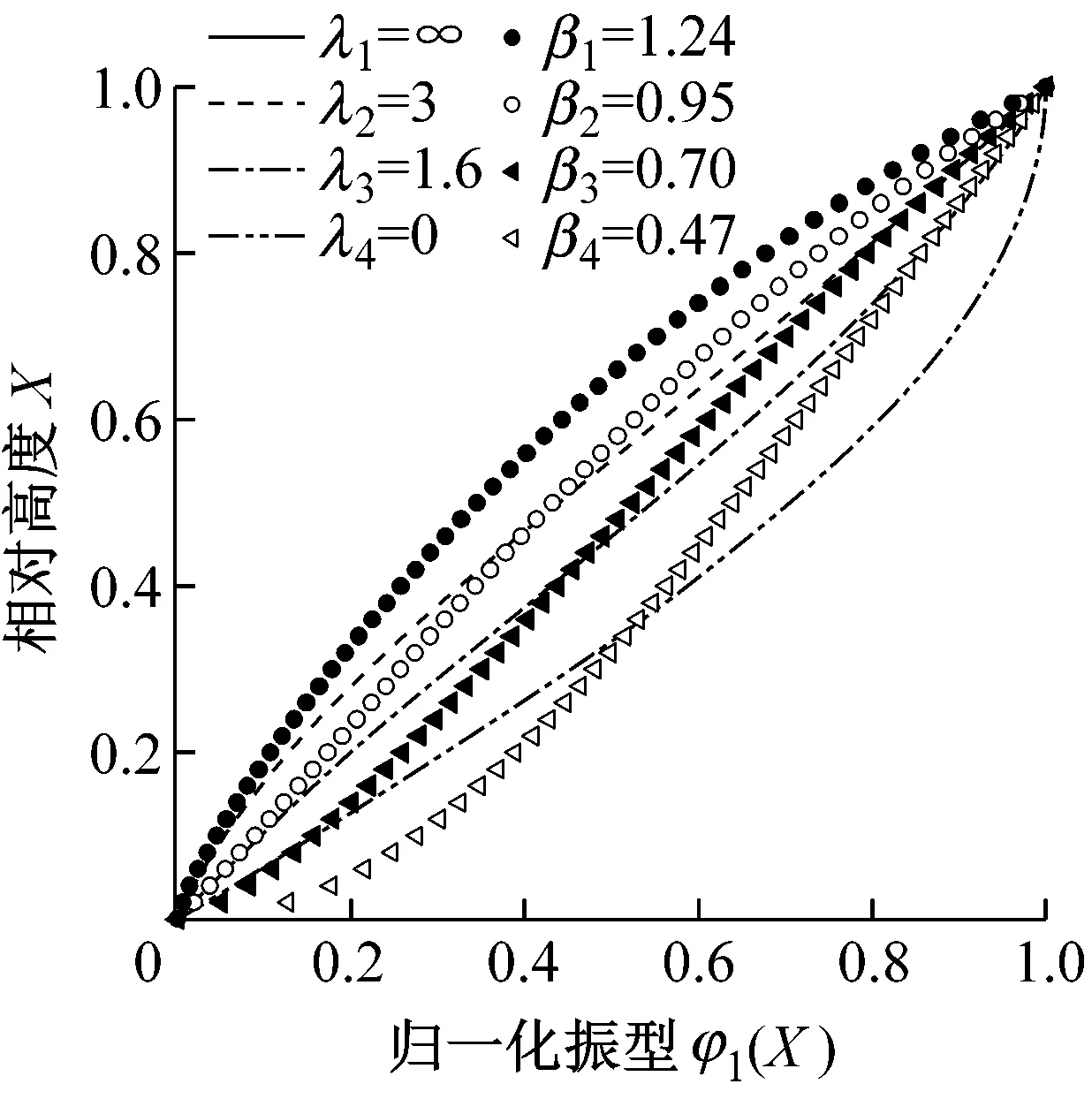
d 式(15)的拟合效果

e 式(16)的拟合效果

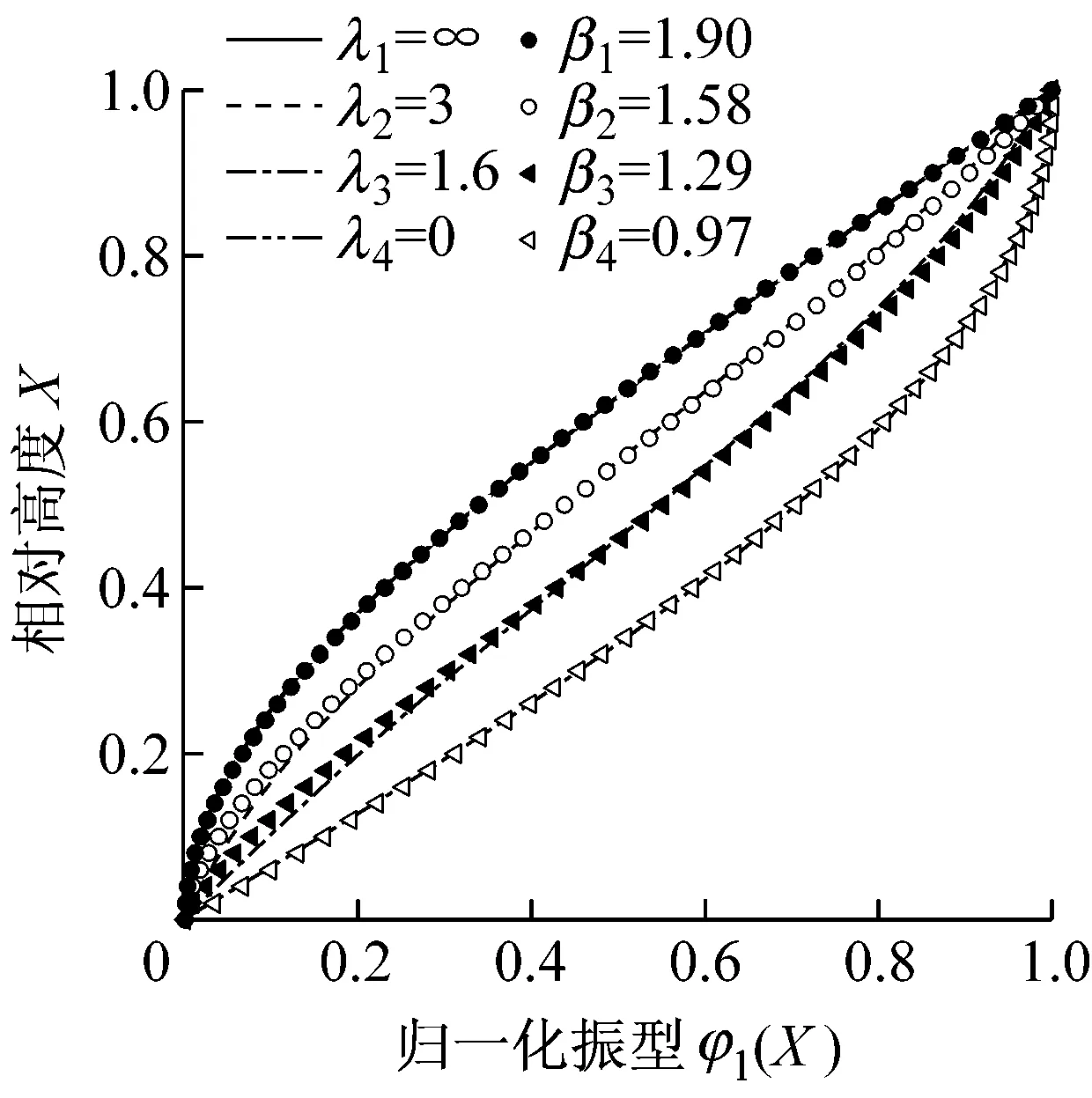
f 式(17)的拟合效果

考虑到β随λ趋于无穷时的收敛性，本文选取如下的反正切函数来拟合二者之间的近似关系式：

β(λ)=1.29+0.4arctan(0.67λ-1.1)

(18)

拟合效果如图3中虚线所示.可见，近似关系式与实际关系式误差基本都在1%内.

表2 结构特征参数λ与振型指数β之间的关系

由此，就给出了确定本文简化振型的完整方案：① 根据实际结构求出结构特征参数λ；② 将λ值代入式(18)得到振型指数β；③ 再将β代入式(17)，即可得到与实际结构更吻合的简化振型，即：φ1=1.5Xβ(λ)-0.5X3.

上述方案的前提是需要事先确定结构特征参数λ，这需要计算实际结构的整体抗弯刚度和抗剪刚度.在实际工程中，这样计算λ不一定很方便.相反，实际结构的动力特性分析已是工程结构计算的必做项目，固有频率比较容易得到.为此，本文给出第二种确定β值的方案：利用结构前两阶固有频率直接计算β值.

图3 结构特征参数λ与振型指数β的关系

从式(10)可知，结构前两阶固有频率计算式如下：

(19)

(20)

若是考虑结构的前两阶频率比γ=ω2/ω1，由于k11H和k12H都是λ的函数，则频率比γ与λ之间存在一一对应关系，根据γ值即可确定λ值，二者关系如图4所示.

为简洁起见，联立图3中的实线与图4曲线这两条关系曲线，直接根据λ这个“桥梁”，也可得出频率比γ=ω2/ω1(周期比T1/T2)与β的关系曲线，如图5所示.经拟合，二者关系可用式(21)表示:

β=15.15(γ-2.95)0.015-13.508

(21)

这样，只需知道频率比γ，即可求出β，从而确定振型.

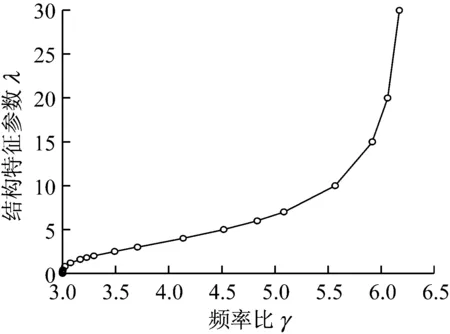
图4 频率比γ与结构特征参数λ的关系

图5 频率比γ与振型指数β的关系

3 某高层建筑风振计算实例分析

某超高层建筑，共44层，其中地面以上为38层，总高度为180.3 m，框架核心筒结构体系；矩形截面，X方向迎风宽度Lx=52 m，Y方向迎风宽度Ly=59.2 m.结构的建设场地为C类地貌，基本风压为w0=0.601 KN·m-2；取结构的体型系数为μs=1.38，一阶振型阻尼比为0.04.根据设计单位通过有限元软件计算提供的结构动力特性资料，其一阶周期分别为T1x=4.709 s、T1y=4.550 s，二阶周期分别为T2x=1.434 s和T2y=1.108 s.

将通过有限元计算得到的振型作为实际振型，以地面处为固定端，沿X、Y方向的振型如图6中的实线和虚线所示.根据已知周期计算出沿X、Y方向的频率比γ分别为3.284、 4.107，代入式(21)可得振型指数βx= 1.395、βy= 1.675，再由式(17)分别可得到两个方向的基阶简化振型，如图6中圆点曲线所示.可见，本文简化振型都能很好地反映实际结构沿X、Y方向的振型.

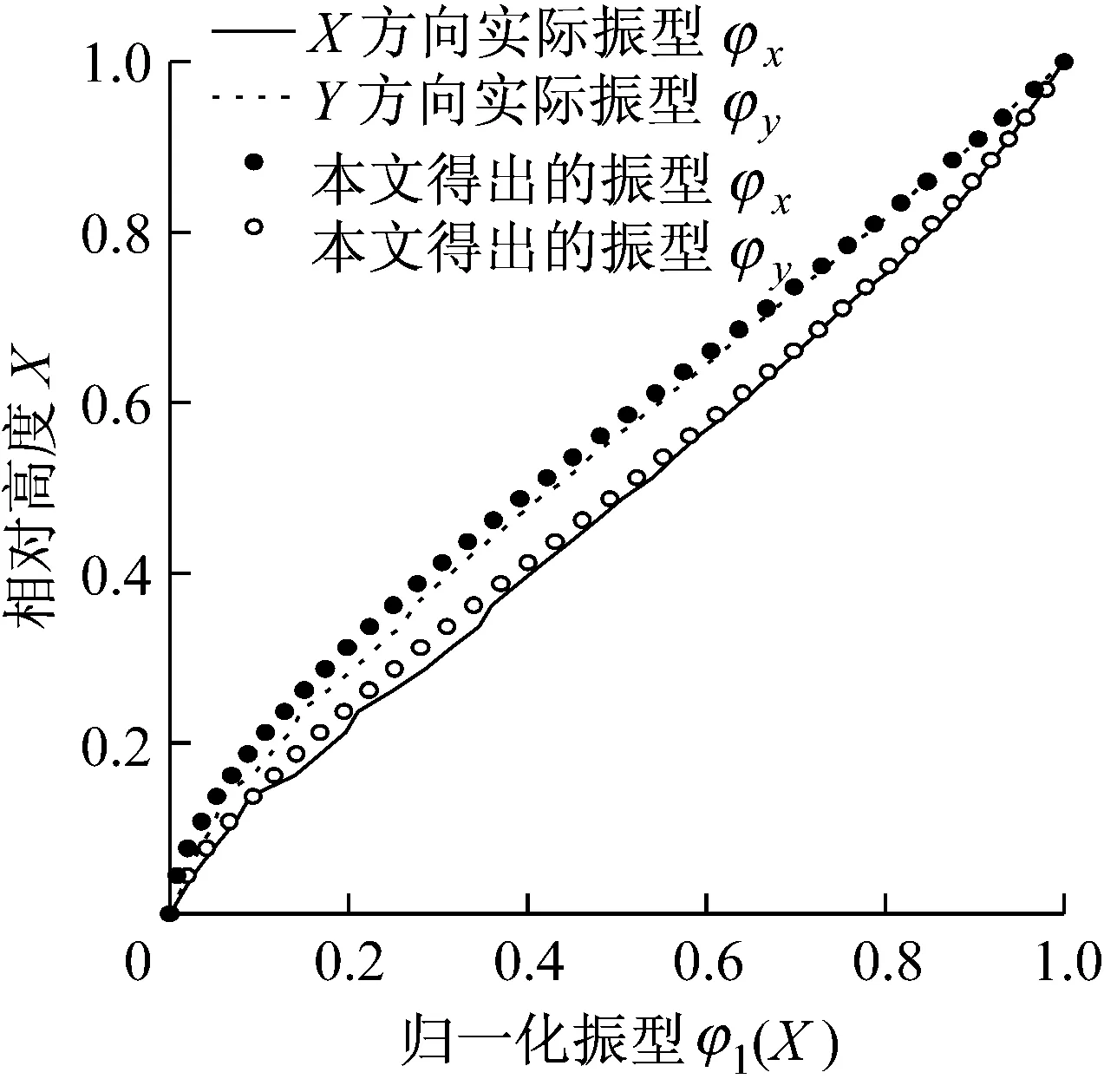
图6 本文振型与实际振型的比较

Fig.6Comparisonbetweenstructuralmodesobtainedbyfiniteelementmethodandbysimplifiedmodelofthispaperrespectively

分别选用实际结构基阶振型、荷载规范[11]的两种振型(即式(3)和规范[11]中表G.0.3给出的振型)、线性振型(即式(1))、正弦振型(即式(4))以及本文简化振型，按我国荷载规范[11]计算该建筑顺风向的等效静力风荷载(ESWL)、底部总剪力和总弯矩.

根据规范[11]的式(8.4.3)可求得不同振型下的风振系数，并进一步得到顺风向等效静风荷载沿高度的分布.图7a给出了分别采用5种简化振型得到的X方向等效静风荷载与采用实际振型所求得的等效静风荷载之间的误差；图7b则为Y方向的误差.图7曲线标注中编号1～5依次代表基于规范[11]表G.0.3给出的振型、正切振型、线性振型、正弦振型、本文振型计算风荷载的误差.可见，采用本文简化振型求得在X、Y两个主轴上各高度处的等效静风荷载最大误差均在3.5%之内，而采用其他4种振型的最大误差均大于11%，甚至可达20%.显然，采用本文的简化振型更能精确地体现风荷载沿高度的分布情况.

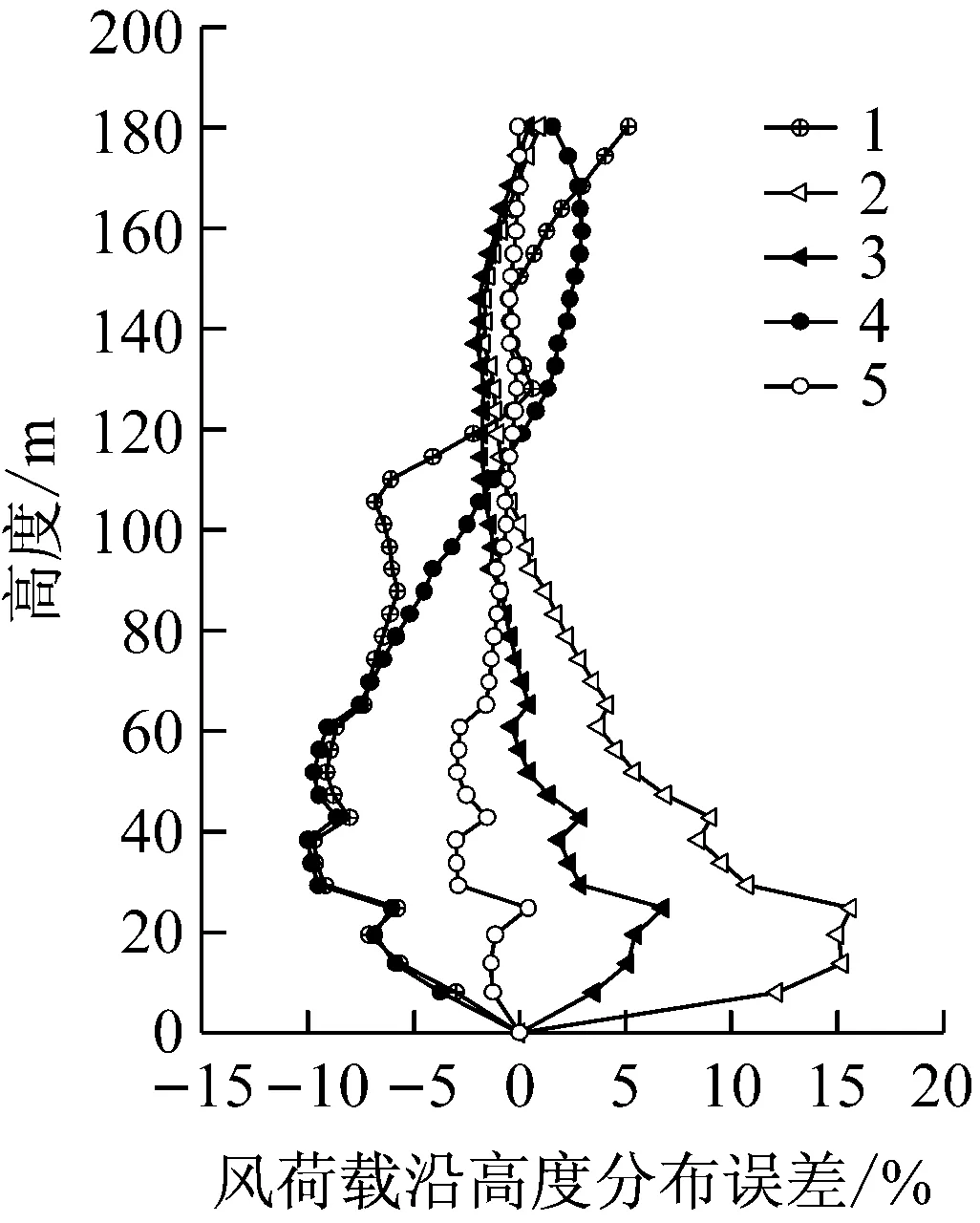
a X方向

b Y方向

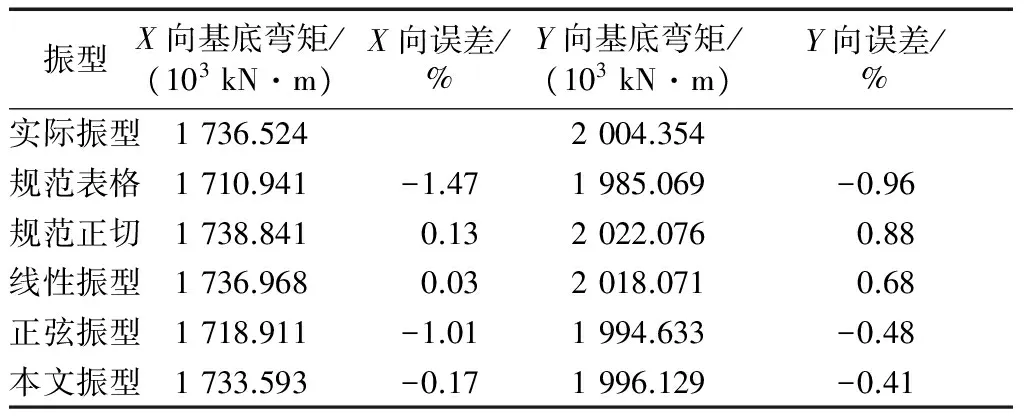
表3、表4给出了基底剪力和基底弯矩的计算结果.可见，采用本文简化振型时，两个方向的计算结果误差都在1%之内，而采用规范表格振型、规范正切振型、线性振型、正弦振型时，基底剪力最大误差依次为3.04%、3.34%、2.08%、2.56%.因此，采用本文的简化振型可以明显地提高风荷载计算的精度.

表3X、Y方向基底剪力比较

Tab.3ComparisonofbaseshearsinXandYdirectionscorrespondingtovarioussimplifiedmodes

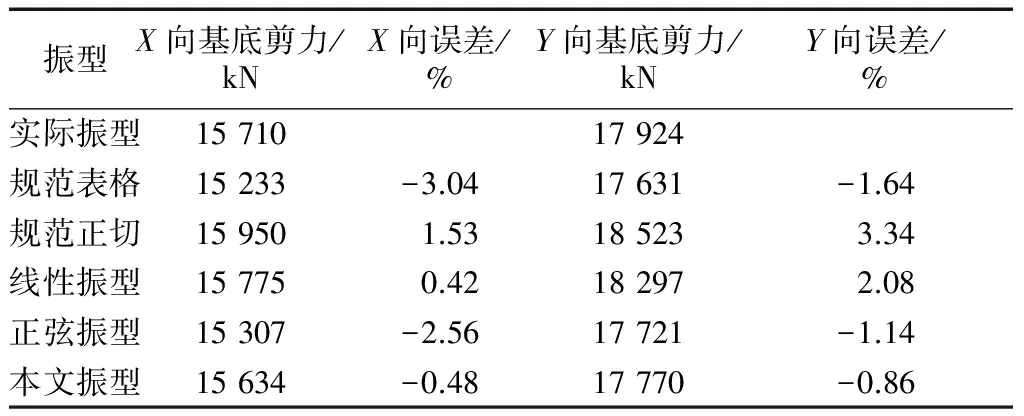
振型X向基底剪力/kNX向误差/%Y向基底剪力/kNY向误差/%实际振型1571017924规范表格15233-3．0417631-1．64规范正切159501．53185233．34线性振型157750．42182972．08正弦振型15307-2．5617721-1．14本文振型15634-0．4817770-0．86

表4X、Y方向基底弯矩比较

Tab.4ComparisonofbasemomentsinXandYdirectionscorrespondingtovarioussimplifiedmodes

振型X向基底弯矩/(103kN·m)X向误差/%Y向基底弯矩/(103kN·m)Y向误差/%实际振型1736．5242004．354规范表格1710．941-1．471985．069-0．96规范正切1738．8410．132022．0760．88线性振型1736．9680．032018．0710．68正弦振型1718．911-1．011994．633-0．48本文振型1733．593-0．171996．129-0．41

事实上，为验证本文简化振型的通用性，本文作者另外从有关资料收集了10组由有限元计算得到的高层建筑基阶振型，建筑高度在60～300 m之间，近似满足等截面均质假定.分析结果表明，根据式(17)直接对这10组振型拟合，也十分吻合；基于本文给出的简化振型确定方案进行风振计算，结果误差也都很小.限于篇幅，在此不一一展示计算结果.

4 结束语

本文通过弯剪型悬臂梁模型的自由振动分析，得出可用于高层建筑的振型函数和控制振型形状的结构特征参数λ；通过对不同λ值得出的基阶振型曲线进行非线性拟合，给出式(17)的简化振型.其形式简单，融合了以往文献中简化振型的优点，对实际高层建筑的基阶振型也具有很好的吻合度.同时，给出了控制简化振型形状的参数β的确定方案，使简化振型能够有效地反映不同建筑结构的基阶振型.将本文简化振型运用到实际高层建筑的风振计算中，结果表明，该振型能更为精确地反映风荷载沿建筑高度的分布情况，明显提高风荷载和风振响应的计算精度.

基于本文振型简化思路，可以再进一步分析高层建筑的扭转振型以及二阶平动振型的简化形式，从而为我国高层建筑结构的风荷载和风振计算提供更科学的依据.同时，对高层建筑抗震设计中地震力的初步预估也有参考价值.

需要说明的是，本文的研究成果只适用于具有任意形状对称截面(质心与刚心重合)的等截面高层建筑.对于变截面、具有弯扭耦合效应、非悬臂型等其它形状的高层建筑，则还有待进一步研究.

[1] 张相庭. 结构风工程:理论·规范·实践[M]. 北京: 中国建筑工业出版社, 2006.

ZHANG Xiangting. Structural wind engineering: theory, code, practice [M]. Beijing: China Building Industry Press, 2006.

[2] 梁枢果, 李辉民, 瞿伟廉. 高层建筑风荷载计算中的基本振型表达式分析[J]. 同济大学学报(自然科学版),2002, 30(5):578.

LIANG Shuguo, LI Huimin, QU Weilian. Analysis of fundamental mode shape expressions of tall buildings for evaluating wind loads [J]. Journal of Tongji University (Natural Science), 2002, 30 (5): 578.

[3] 周印. 高层建筑静力等效风荷载和响应的理论与实验研究[D]. 上海:同济大学, 1998.

ZHOU Yin. Theoretical and experimental study of high-risebuilding static equivalent wind loads and response [D]. Shanghai:Tongji University, 1998.

[4] HOLMES J D．Mode shape corrections for dynamic response to wind [J]．Engineering Structures，1987，9(3)：210.

[5] ZHOU Y, GU M, XIANG H. Alongwind static equivalent wind loads and responses of tall buildings. part II: effects of mode shapes[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1999, 79(1-2):151.

[6] 周印, 顾明, 江欢成,等. 高层建筑气动模型的模态形状修正[J]. 工程力学, 1999, 16(4):33.

ZHOU Yin, GU Ming, JIANG Huangcheng,etal. Mode shape corrections for aerodynamic model of tall buildings [J]. Engineering Mechanics , 1999, 16(4):33.

[7] American Society of Civil Engineers (ASCE). Minimum design loads for buildings and other structures [S]. Reston (VA): ASCE, 2010.

[8] European Committee for Standardization (CEN). Eurocode 1: actions on structures-part 1-4: general actions—wind actions: EN 1991-1-4:2005/ AC:2010 (E)[S]. [S.l.]: European Committee for Standardization (CEN), 2010.

[9] Architectural Institute of Japan (AIJ). RLB recommendations for loads on buildings [S]. Tokyo: Structural Standards Committee, Architectural Institute of Japan, 2004.

[10] 张军锋, 葛耀君, 柯世堂,等. 中美日三国规范高层结构风荷载标准值对比[J]. 湖南大学学报(自然科学版), 2011, 38(10):18.

ZHANG Junfeng, GE Yaojun, KE Shitang,etal. Comparative study on the nominal value of wind loads on tall buildings among the codes of China，American and Japan [J]. Journal of Hunan University(Natural Science), 201l, 38(10) :18.

[11] 中华人民共和国国家标准.建筑结构荷载规范:GB50009—2012[S]. 北京:中国建筑工业出版社, 2012.

China National Standard. Load code for the design of building structures: GB 50009—2012[S]. Beijing: China Building Industry Press, 2012.

[12] 徐永林, 朱元清, 周晶矛,等. 超高层建筑风荷载计算中的振型函数[J]. 地震地磁观测与研究, 2010, 31(3):111.

XU Yonglin, ZHU Yuanqing, ZHOU Jingmao,etal. Model function for computation of wind load on the skyscraper [J]. Seismological and Geomagnetic Observation and Research, 2010, 31(3):111.

[13] 李永贵，李秋胜. 基本振型对高层建筑等效静力风荷载的影响分析[J]. 地震工程与工程振动, 2016, 1(6):38.

LI Yonggui, LI Qiusheng. Influence of fundamental mode shapes on equivalent static wind loads of tall buildings [J]. Earthquake Engineering And Engineering Dynamics, 2016, 1(6):38.

[14] S. 铁摩辛柯，J. 盖尔.材料力学[M]. 北京：科学出版社, 1978.

TIMOSHENKO S, GERE J. Mechanics of materials[M]. Beijing: Science Press, 1978.

[15] 陈国兴, 金永彬, 宰金珉. 高层建筑随机地震反应的简捷计算[J]. 南京建筑工程学院学报(自然科学版), 1999(1):29.

CHEN Guoxing, JIN Yongbin, ZAI Jinmin. A simple method of random earthquake response analysis for high-rise buildings [J]. Journal of Nanjing Architectural and Civil Engineering Institute(Natural Science), 1999 (1): 29.