高等代数在数学分析极值问题中的应用

何林海

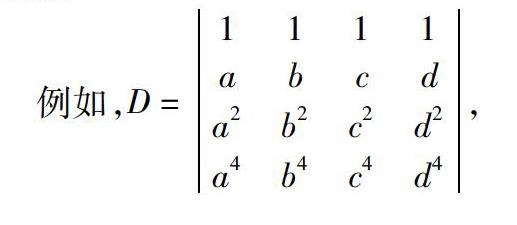
【摘要】 在我国的高等教育中，高等数学是一门基础学科，高等数学的学习较为复杂，难度系数相比初高中数学学习来说也较大.本文通过高等代数在数学分析极值中的研究，提出更适合高等学校数学教学的方案和教学内容，提高教学质量，提升学生学习效率.

【关键词】 高等代数;数学分析;极值

高等代数在数学分析极值中的应用是为了更简单的计算出函数极值，传统的极值计算方法，较为复杂，容易出错，耗费大量的时间，通过高等代数的方式，可以使极值的计算变得相对简单，提高学习效率，避免浪费教学时间，提高教学质量.关于高等代数求极值的方式很多，需要学生掌握一定的基础知识.高等代数本就是一门较难的学科，学生在学习过程中会因为难度较大，课程枯燥，失去学习的信心和兴趣，产生厌学的心理，不利于教学质量的提高.在教师进行教学研究时，应该注意学生学习兴趣的培养，让高等代数在数学分析极值中的应用发挥其真正的作用，全面地提高学生学习效率，达到提升教学质量的效果.

一、高等代数

高等代数是高等数学教学的重要组成部分，主要由两大部分构成.多项式代数，也就是二次以上的一元多项式方程.关于一元多项式方程的概念，一元多项式代数的定义：a nx n +a  n-1 x n-1 +…+a 1x+a 0，其中a 0，a 1，…，a n∈P，叫作数域P上的一元多项式代数，通常用f（x），g（x），h（x）等来表示，即f（x）=a nx n +a  n-1 x n-1 +…+a 1x+a 0.线性代数，在高等代数的学习中，线性代数是一次方程组的延伸，是高等代数中的一个重要分支.线性代数中的“线性”所指的是一种数学关系，其变形形式为f（x+y）=f（x）+f（y），线性代数由多个内容组成，其中包括矩阵和行列式，矩阵和行列式 都是高等代数学中的常用工具，对高等代数的学习十分重要.

二、数学分析极值

极值是在高等数学分析中，求函数的最小值或最大值，也就是数学函数的一个稳定值.极值作为一个稳定值，在数学分析中有一个具体的定义，通常情况下，如果函数f（x）在x 0的区域P中具有定义，并且在区域P内除x 0的所有的点，都符合f（x）f（x 0），那么在数学分析中把f（x）极小值称作f（x 0）.极值的应用广泛，并在数学学科上具有重要意义，因此，数学分析极值的应用，一直是重要的研究课题.高等教育的数学分析极值含义较深，学生对数学分析极值理论难以理解，学习难度高，目前，在极值的计算中，高等代数的方式可以有效地提升函数极值的计算速度.

三、高等代数在数学分析极值问题中的应用

（一）线性代数中行列式的应用

运用行列式求极值，格式明了，算法相对简单，简单举例说明.

例如，D=  1 1 1 1a b c da2 b2 c2 d2a4 b4 c4 d4  ，

解作，D1=（b-a）（c-a）（d-a）（c-b）（d-b）（d-c）（x-a）（x-b）（x-c）（x-d）.

故D=（a-b）（a-c）（a-d）（b-c）（b-d）（c-d）（ a+ b+c+d）.

行列式在数学分析极值问题中的应用较多，行列式的数学分析极值运算，注意其行列式的规律和特点，寻求科学有效的方法，提高效率.

（二）多项式代数在极值问题中的应用

多项式代数在极值问题中的应用，是求函数极值的多种方式里的一种，其出现的机会不多，但对于高等数学教育的学习来说，掌握多项式代数在数学分析极值中的应用，也是必要的.多项式代数在极值问题中的应用无论是在学科理论上还是实际的运用中都具有十分重要的位置，加强多项式代数的教学是高等数学教育的重要内容.

例题  假如函数f（x）=x3+x+1可约，则函数f（x）具有一个一次因式和一个二次因式，问该如何证明？证明： f（x） 的导数f′（x）=3x2+1>0恒成立，所以f（x）为单调递增函数 f（0）= 1，f（-1）=-1，f（0）f（-1）<0，所以f（x）在（-1，0）上有唯一实数根，设为a，f（x）=（x-a）g（x），且 g（x）= 0在 R 上无解，则f（x）=（x-a）（x2+bx+c）.

加强多项式代数在极值问题中的实际应用，提高學生对高等代数的运用，提升教育教学质量，实现高等教育培养学生全面发展的目标.

（三）正交变换在数学分析极值问题中的应用

在多元函数的极值应用上，正交变换的应用，可以有效地提高学习效率，提高学生学习成绩.在部分多元函数的计算上，因为多元函数的计算量大，过程复杂，因而，在多元函数的教学课堂上，学生经常出现听不懂课堂内容，解答不出课堂习题的情况，这种情况下适当引用正交变换的解答方法，可以把复杂的多元函数简单化，让学生更容易理解其解题思路，了解多元函数，从而可以在课堂上轻松地完成课堂内容，提高学生的课堂学习效率，实现教学的目的.

四、结 语

随着国家现代化的发展，国家对人才的需求量日益增大，国家重视人才的全面发展，意味着高校的教育也需要注重学生的全面发展.在经过小学到高中的数学学习后，为高等教学中的数学学习打下了良好的基础，高等数学的学习是对数学的深入研究学习.其学习难度较大，需要对教学方法进行不断的研究和革新，以达到最佳的教学效果，提高教学质量，促进学生的全面发展.为了实现这些目标，研究高等代数在数学分析极值中的应用，并将研究结果运用到教学实际中，对教学事业起到了重要作用.

【参考文献】

[1]旷雨阳.谈谈数学分析与泛函分析的某些递进关系[J].科技通报，2013（3）：20-22.

[2]严子谦，尹景学，张然.数学分析中的方法与技巧[M].北京：高等教育出版社，2009.