部分非线性指标模型的降维及在医疗费用评估中的应用*

冯 彦 徐 璇 赵晓兵△

·方法介绍·

部分非线性指标模型的降维及在医疗费用评估中的应用*

冯 彦1徐 璇2赵晓兵2△

分析和研究医疗费用最重要的目的是寻找和确定与医疗费用密切相关的重要变量,以达到通过控制这些变量减少医疗费用支出的目的。然而，由于医疗费用数据结构复杂、附加信息(协变量)的高维、以及医疗费用数据往往是严重偏斜、异方差、非正态等等,给医疗费用的研究带来了巨大的统计挑战。因此,寻找一种创新的统计建模方法和统计分析技术来分析医疗费用显得非常必要。

就目前已有的文献而言,对医疗费用的建模主要可分为两类,一类对于医疗总体费用进行建模,另一类是对于纵向医疗数据进行建模。其中对于纵向医疗数据分析,很多学者提出了不少相关的模型[1],例如,边际模型[2-3]、马尔科夫转换模型[4]以及随机(固定)效应模型[5]等等。近年来,广义线性模型也引起了很多学者的广泛讨论[6]。但是,这种方法不能很好地考虑医疗费用的相关性,并且对与时间有关的变量的作用不能够很好地进行解释[7]。最近,Chen等拓展了经典的广义线性模型[2-3],将一些随着时间变化的协变量通过非线性函数的形式加到广义线性模型中,却仍然假设该模型中的连接函数是已知的。

为了使得上述模型更加灵活,最大效率地利用收集到的医疗费用的高维辅助信息,本文尝试将Chen等的广义线性模型中的连接函数放松为未知函数[3],进而提出了“部分非线性指标模型”(PNIM)如下:

(1)

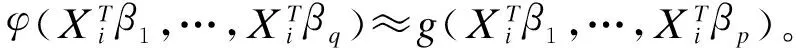
估计方法

对于给定的维数q，MAVE降维的思想就是通过局部线性光滑技术同时估计参数和非参数部分,再比较不同维数下的回归函数的残差，从而挑选出合适的维数。该方法极大地提高了对复杂数据的有效维空间的估计。下面介绍具体参数βj(j=1,2,…,p)以及非参数部分g(·)和f(·)的估计方法和子空间维数及窗宽的确定方法。

1.降维空间基方向和非参数部分的估计

(2)

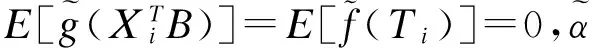
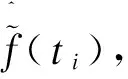
(3)

文献[7]指出wij的选择对降维结果至关重要,通常选取

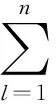
(4)

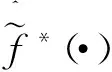
(5)

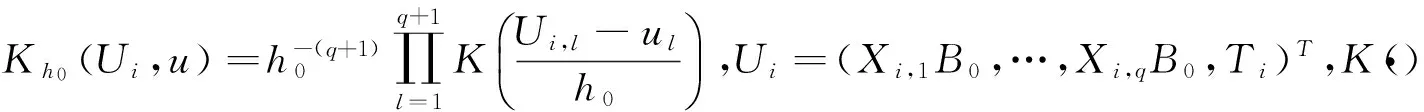
(6)

正如Zeger和Liang指出的那样[7]，权重wij会依赖于B。本文参照Xia给出两种权重的选取[8]：

(1)初始权重

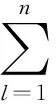
(7)

(2)精确权重

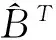
(8)

2.降维子空间的维数及窗宽

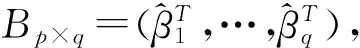
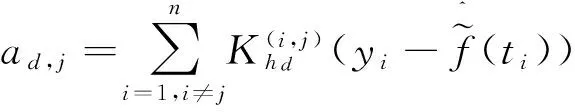
3.算法及修正

下面给出利用改进的MAVE方法求解的算法：

Step1(基):对于任意q，1≤q≤p,则在q维子空间的基可由下面步骤求出:

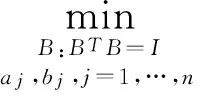
(9)

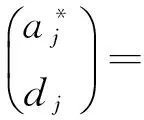
Step2(维数)：求得CV(d),0≤d≤p,找出最小的CV(d)所对应的维数d,由此对应的Step1-(3)求出的B即为估计的子空间的基。

数值模拟

我们采用MATLAB软件考虑如下两个模型的数值模拟。

情形一：考虑一维的情形q=1,我们利用下面模型来产生样本

其中,Ti服从[0,1]均匀分布,Xi分两种情况讨论,εi独立同分布服从N(0,1)。故此时模型满足E[f(T)]=E[1.5sin(2πT)]=0,同时假设(X,T)与ε相互独立。

下面根据Xi的两种分布情况进行讨论:

情形二：考虑二维情形q=2，β1=(1,0,…,0)∈R10，β2=(0,0,…,1,0)∈R10,此时,我们利用下面模型

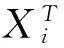
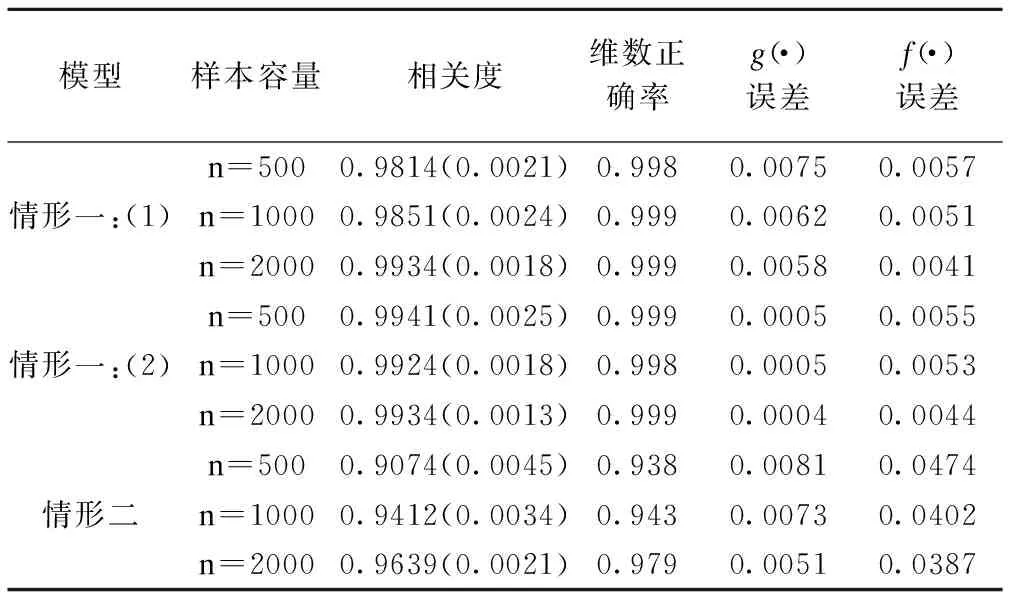
表1 推广的MAVE的数值模拟结果

由表1,可以发现β的估计值与真值有很高的相关性。同时可以发现本方法对于结构维数有很好的估计。第四列显示,维数选择的正确率非常高。与此同时,对非参数部分g(·)与f(·)的估计误差也比较合理。

下面给出对非参数部分的估计图像。图1至图6分别为情形一非参数部分g(·)、f(·)的估计,以及情形二的非参数部分f(·)在γ=0.2在γ=0.8的估计。图中实线为非参数部分的真实曲线,点画线为其相应的估计曲线,虚线为95%的置信曲线。从图3～6可以发现,本文提出的估计方法也能够很好地估计出非参数部分。

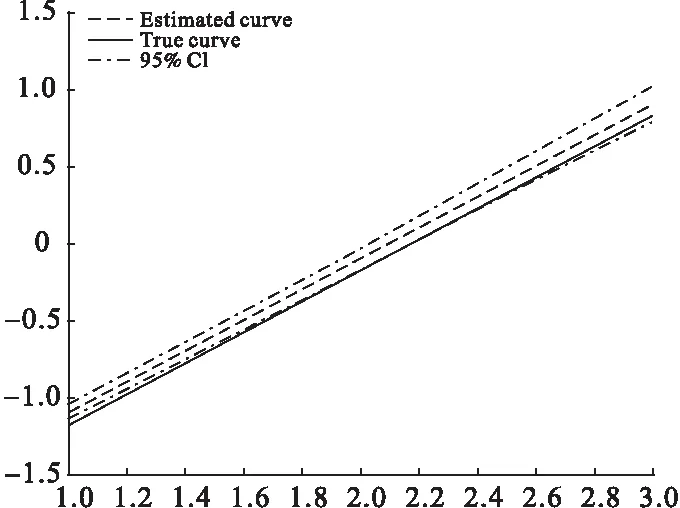
图1 情形一(1)的g(·)的拟合图

实例分析

下面针对收集得到的医疗费用纵向数据进行分析。医疗费用数据是美国全国性医疗卫生服务抽样调查得到的,包括受访者的健康状况、基本信息、医疗卫生服务、卫生支出、医疗保险等信息。通过对这些数据分析有助于保险公司制定方案，也有助于政府制定医疗政策。

图2 情形一(1)的f(·)的拟合图

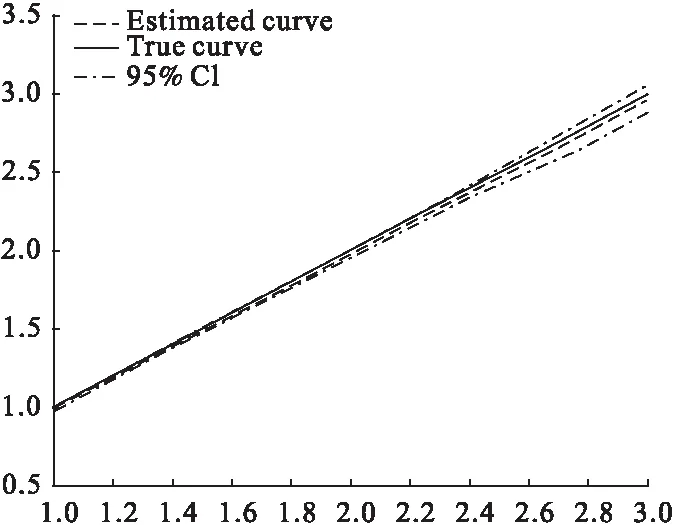
图3 情形一(2)的g(·)的拟合图

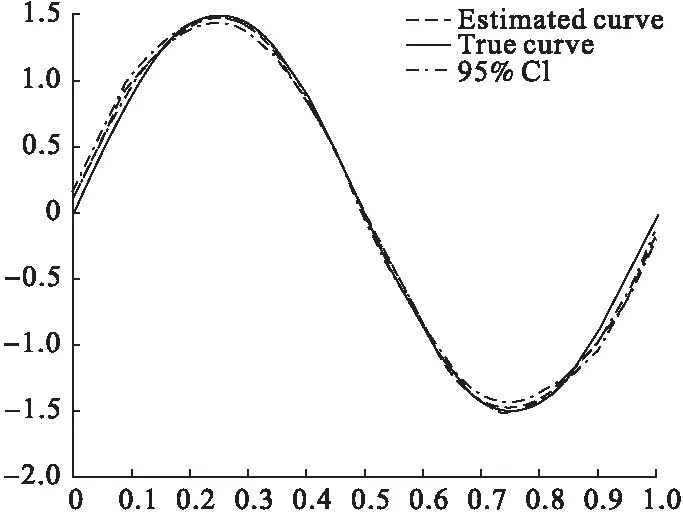
图4 情形一(2)的f(·)的拟合图

图5 情形二γ=0.2的f(·)的拟合图

图6 情形二γ=0.8的f(·)的拟合图

本文研究的MEPS(TheMedical Expenditure Panel Survey,MEPS)是2010年全年调查中老龄化家庭的医疗数据，这些家庭的成员年龄都在65岁至84岁之间，总共收集到医疗数据样本2139个。通过对医疗数据的简单分析，医疗费用数据往往是高度右偏的，均值很大(9235美元)，但是中位数很小(3955美元)。Chen等在建立模型分析医疗费用数据时[2]，只选取了部分协变量分析，例如性别、种族、疾病等。但是我们发现收集到的医疗费用数据含有大量的信息，拥有大量的协变量，选取部分协变量不能全面进行医疗费用的分析。因此，本文除了考虑年龄对医疗费用的影响即模型中的f(·)，还考虑了14个协变量对医疗费用的影响，即种族、性别、死亡、住院情况、心血管疾病、呼吸道疾病、身体运动障碍、癌症、糖尿病、家庭成员情况、附加保险情况、家庭收入等级、医疗保险报销情况、教育程度。通过建立部分非线性多指标模型，充分考虑14个协变量以及年龄对医疗费用的影响。

利用本文提议的模型和方法对美国MPES-2010数据进行分析，根据CV(q)最小，选出维数为q=2。从而得到降维子空间的基(即模型(1)中的β1,β2) 见表2。通过表2中列向量数值的大小和正负，我们发现,“是否住院”的情况对医疗费用的影响最大。此外,死亡、心血管疾病、呼吸道疾病、癌症、医疗保险情况、医疗报销情况都对医疗费用有着较大的影响。

与此同时，我们还得到年龄对医疗费用的影响，如图7,虚线为年龄对医疗费用的影响估计曲线，点画线为95%的置信曲线。

表2 降维子空间(降维结果)

从图7可以发现一开始随着年龄的增加,医疗费用有所降低，而后在67岁到69岁,医疗费用有着较大的上升；随后在69到73之间，医疗费用会随着年龄的增长在一定的范围内波动，随后到74附近达到一个小峰值；之后有所下降，在75岁到80岁附近，随着年龄的增长波动向上递增；然后在81岁到82岁附近医疗费用会有所下降，随后医疗费用又随即快速上升。

图7 实例的f(·)估计图

[1] 曲艺,吴晶.骨质疏松髋部骨折患者医疗资源使用与医疗费用研究.中国卫生统计，2016,33:430-432.

[2] Chen JS,Liu L,Zhang D,et al.A flexible model for the mean and variable functions,with application to medical cost data.Statistics in Medicine,2013,32:4306-4318.

[3] Chen JS,Liu L,Shih,YCT,et al.A flexible model for correlated medical costs with application to medical expenditure panel survey data.Statistics in Medicine,2016,35:883-894.

[4] Castelli C,Combescure C,Foucher Y，et al.Cost-effectivenessanalysis in colorectal cancer using a semi-Markov model.Statistics in Medicine,2007,26:5557-5571.

[5] Liu L.Joint modeling longitudinal semi-continuous data and survival,with application to longitudinal medical cost data.Statistics in Medicine,2009,28:972-986.

[6] Carroll RJ,Fan JQ,Gijbels I,et al.Generalized partially linear single-index models.Journal of the American StatisticalAssociation,1997,92:47-489.

[7] Zeger SL,Liang KY.An overview of methods for the analysis of longitudinal.Statistics in medicine,1992,11:1825-1839.

[8] Xia YC.A multiple-index and dimension reduction.Journal of the American Statistical Association,2008,103:1631-1640.

[9] Xia YC.Hardle W.Semiparametric estimation of partially linear single-index models.Journal of Multivariate Analysis,2006,97:1162-1184.

[10] Kim W,Linton OB,Hengartner NW.A computationally efficient oracle estimator for additive nonparametric regression with bootstrap confidence intervals.Journal of Computational and Graphical Statistics,1999,8:278-297.

国家自然科学基金资助项目(11271317)；浙江省自然科学基金资助项目(LY16A010007)

1.山西医科大学第一临床医学院，公共卫生学院，护理学院(030001) 2.浙江财经大学数据科学学院

△通信作者：赵晓兵，Email:maxbzhao@126.com

张 悦)