Cox比例风险回归模型的贝叶斯估计方法研究*

张继巍 高文龙 李学朝 拉扎提·木拉提 秦天燕 李娟生

兰州大学公共卫生学院流行病与卫生统计学研究所(730000)

Cox比例风险回归模型的贝叶斯估计方法研究*

张继巍†高文龙†李学朝 拉扎提·木拉提 秦天燕 李娟生△

兰州大学公共卫生学院流行病与卫生统计学研究所(730000)

Cox比例风险回归模型是目前进行多因素生存分析最常用的半参数模型，由于其兼有参数模型和非参数模型的优点，并可以在数据不完全的情况下分析研究对象生存时间的影响因素，因而得到了广泛的应用[1]。而贝叶斯统计分析方法可以有效利用先验信息，在小样本数据推断中具有明显优势[2]，其在生存分析中也得到了广泛应用，比如Jennifer和Mike实现了贝叶斯在Weibull模型中的应用[3]，Lee等人实现了贝叶斯方法在生存数据指数分布中的应用[4]。因此将两者结合对Cox回归模型进行贝叶斯估计可以有效的处理小样本、数据不完全和运行环境复杂等问题[5]，在生存分析中具有广阔的发展前景。

本文对生存分析模型中的Cox比例风险回归模型基于贝叶斯条件下的无信息先验分布，对小样本、随机截尾和删失的不完全数据，结合马尔科夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)方法中Gibbs抽样思想，利用OpenBUGS软件[6]进行估计，研究该模型在OpenBUGS环境下的建模过程，最后结合生存数据对该模型进行应用研究。

贝叶斯Cox比例风险回归模型原理

贝叶斯Cox比例风险回归模型是在原Cox回归模型[7]的基础上，利用贝叶斯统计分析方法的基本原理对其回归参数进行估计。该方法将模型中各估计参数看成随机变量，并对其指定适当的先验分布，再结合样本信息，通过Gibbs抽样MCMC模拟计算其后验分布，最终实现模型参数的估计。我们假设有i个观测对象和p个潜在影响因素，则Cox回归模型的基本形式为[8]：

h(t,Xi)=h0(t)exp(β1X1+β2X2+…βpXp)

(1)

式中h(t,X)是具有协变量X的个体在时刻t时的风险函数；第i个对象的生存时间为ti；协变量X=(X1，X2，…,Xp)是影响生存时间的p个有关因素，这些变量可以是定量的，也可以是定性的，在整个观测期间内不受时间的影响；h0(t)是所有协变量取值为0时的风险函数，称为基线风险函数；βi=(β1,β2,…,βp)为Cox模型的回归系数，是一组待估计的回归参数；在贝叶斯分析中，需要先对这些参数指定适当的先验分布，通常不合适的先验会对结果产生影响。因此，按照Kalbfleisch and Prentice (1980)，Clayton (1991)，Clayton (1994)等人[9]的建议将Cox回归模型系数βi设定无信息正态先验分布。

βi(i=1,2,…,p)～N(μ,τ)

(2)

式(2)中τ=1/σ2，考虑到该先验分布对参数后验分布的影响，因此设定μ=0，精度τ=0.000001。生存结局Y为0-1指示性变量(如果观测对象的生存时间删失，则Y=0，否则Y=1)。

在OpenBUGS中对该模型进行参数估计时，为了得到更加可靠的后验参数估计，需要设定不同初始值的多条链进行模拟迭代，并且先要确定模型的退火参数burn-in的值，以保证模型在收敛状态下对后验参数进行抽样估计；为了降低各条初始值链之间的自相关性和蒙特卡洛误差，需要设置参数thin值大于1，并需要更多的抽样样本用于参数估计；模型的收敛情况可以通过观测遍历均值、迭代轨迹图和BGR图直观的判断，当它们都趋于稳定时，可以认为模型收敛[9]。

实例分析

Cox比例风险回归模型主要用于影响因素分析、校正协变量后的组间比较和多变量生成预测[8]。本研究选取文献[7]中介绍的例19-5，利用收集的63例某种恶性肿瘤患者的生存数据，通过构建Cox比例风险模型，结合贝叶斯统计分析方法试进行其生存情况的影响因素分析。变量的赋值和数据见原文献[7]。利用贝叶斯统计方法进行Cox回归模型参数估计的步骤如下：

第一步：生存时间的设定

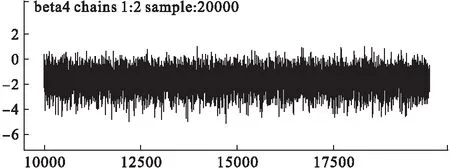
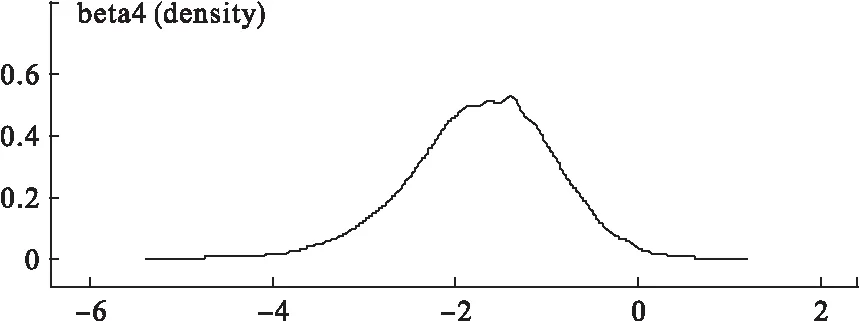
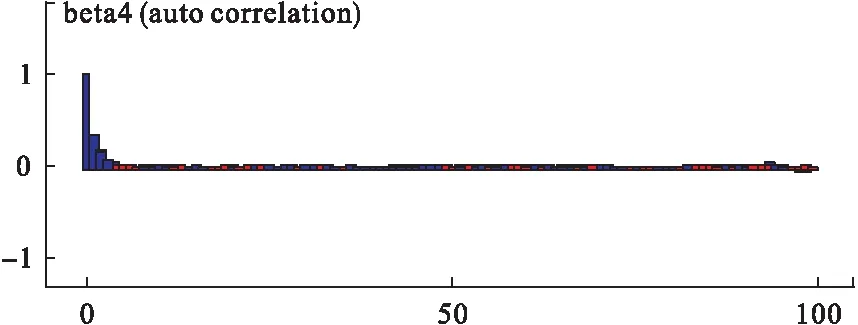
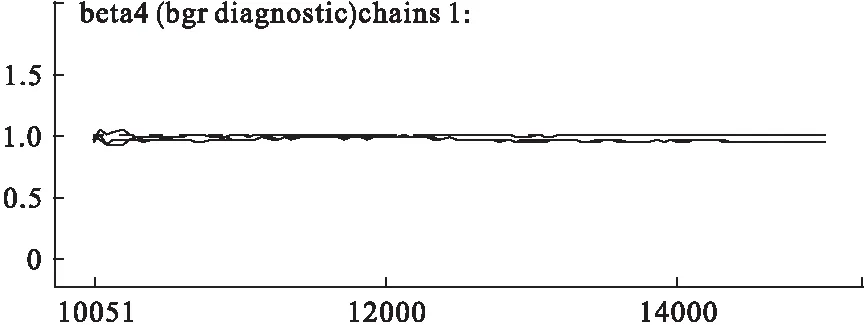
基于贝叶斯条件下的Cox回归模型建立时，我们通常需要把生存时间ti分成J个等距离的时间区间0=a0

本例中，将生存时间ti∈[2,120]分成了16个等距离的区间，即T=16。

第二步：Cox回归模型在贝叶斯条件下的建立：

定义指示变量dNij为第i个观察对象在第j个区间的“生存”情况，则当dNij=0时，个体i在第j个区间的数据是删失的；否则，dNij=1，并取dNij服从参数为Idtij的泊松分布，此时我们建立的Cox模型为：

model{

#指示变量的设定

for(i in 1:N) {

for(j in 1:T) {

O[i,j] <- step(obs.t[i] - t[j] + eps)

# O[i,j]为研究对象i在第j个时间区间的观测情况，通过step(e)这个函数来表示，如果e>=0，O[i,j]=step(e)=1，表示研究对象能被观测到；否则O[i,j]=0，表示已删失。

dN[i,j] <- O[i,j] * step(t[j + 1] - obs.t[i] - eps) * Y[i] } }

# dN[i,j]为O[i,j]在时间区间[t,t+dt)上的增量，和O[i,j]意义一样，当dNij=0时，个体i在第j个区间的数据是删失的；否则，dNij=1。

# Y[i]表示第i个研究对象的生存结局，取值为0或1。如果Y[i]=1，表示出现生存结局；否则Y[i]=0，表示删失。

# Doodle模型的构建

for(j in 1:T) {

for(i in 1:N) {

dN[i,j] ～ dpois(Idt[i,j])

#假设dN[i,j]服从均值为Idt[i,j]的泊松分布

Idt[i,j] <- O[i,j] * exp(β′X) * dh0[j]

#dh0[j]=h0[j]dt为基线风险函数在第j个时间区间上的增量，则有 h0[t]=sum(dh0[1:j])，j=1，2，…，T。

S[i,j] <- pow(exp(-sum(dh0[1:j])),exp(β′X)) #Cox回归模型的生存率函数，其中函数pow(e1,e2)=e1^e2

}

dh0[j] ～ dgamma(mu[j],c) }

mu[j] <- dh0.e[j] * c # dh0.e[j]是未知风险函数dh0[j]的一个先验猜测，c为该先验猜测的精度。

c <- 0.001

r <- 0.1

for (j in 1:T) {

dh0.e[j] <- r * (t[j+1] - t[j]) }

#在该例中，我们设dh0.e[j] <- r *Δt，其中r是对研究对象在每个单位时间内删失率的猜测，Δt表示生存时间分段区间的尺寸，即Δt=t[j+1] - t[j]

#其他先验信息

for (k in 1:6)

Beta[k] ～ dnorm(0.0,0.000001) }

第三步：利用OpenBUGS软件对模型进行贝叶斯估计：通过步骤二构建的模型，结合贝叶斯统计分析工具OpenBUGS软件[6]，对模型中的未知参数进行贝叶斯估计。本例的数据结构如下：

list( N=63,T=16,eps=1.0E-10,

t=c(2,3,4,5,7,12,15,16,18,19,24,26,29,35,40,66,120),

obs.t=c(52,51,35,103,7,60,58,29,70,67,66,87,85,82,76,74,63,101,100,66,93,24,93,90,15,3,87,120,120,120,120,120,120,40,26,120,120,120,3,120,7,18,120,120,15,4,120,16,24,19,120,24,2,120,12,5,120,120,7,40,108,24,16),

X1=c(54,57,58,43,48,40,44,36,39,42,42,42,51,55,49,52,48,54,38,40,38,19,67,37,43,49,50,53,32,46,43,44,62,40,50,33,57,48,28,54,35,47,49,43,48,44,60,40,32,44,48,72,42,63,55,39,44,42,74,61,45,38,62),

X2=c(0,0,0,1,0,0,0,0,1,0,0,1,1,0,1,1,1,1,0,1,0,0,1,0,1,0,1,1,1,0,1,1,0,1,1,1,1,1,0,1,0,0,1,0,1,0,1,0,0,0,1,0,0,1,0,0,0,1,0,0,1,0,0),

X3=c(0,1,0,1,1,1,1,0,1,1,1,0,1,1,1,1,1,0,1,1,0,0,0,0,0,0,1,1,1,1,0,0,0,1,0,1,1,0,0,0,1,0,0,1,1,0,1,0,1,0,0,1,0,0,1,0,0,1,0,1,0,1,0),

X4=c(1,0,0,1,0,0,0,0,1,0,0,1,1,0,1,1,1,1,0,1,0,0,1,1,0,0,1,1,1,0,1,1,0,1,0,0,1,0,0,1,0,0,1,0,0,0,1,0,0,0,0,0,0,1,1,0,0,1,0,0,1,0,0),

X5=c(1,0,1,1,0,0,0,1,0,0,0,1,0,0,0,0,0,1,0,0,1,1,1,1,1,1,1,0,0,0,1,1,1,0,1,0,0,1,1,1,1,1,1,0,0,1,0,1,0,1,1,1,1,1,0,1,1,0,1,1,1,0,1),

X6=c(0,0,1,0,0,0,0,1,1,1,0,0,0,1,1,1,0,1,0,1,0,0,0,0,0,0,1,0,0,1,0,0,0,1,0,0,0,0,0,0,1,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,1,0,0,0,0),

Y=c(0,0,1,0,1,0,0,1,0,0,0,0,0,0,0,0,0,0,0,1,0,1,0,0,1,1,0,0,0,0,0,0,0,1,1,0,0,0,1,1,1,1,0,0,1,1,0,1,1,1,0,1,1,0,1,1,0,0,1,1,0,1,1))

通过Gibbs抽样和马尔科夫迭代，最终得到的结果见表1和图1～5。

表1 基于OpenBUGS的贝叶斯估计结果

图1 迭代历史图

图2 核密度图

图3 自相关函数图

图4 迭代诊断图

图5 迭代轨迹图

本例采用初始值不同的两条链模拟迭代，抛去前10000次抽样以保证样本是从后验分布中抽取，额外的20000次抽样用于参数估计；由图2～5可以看出各链混合较好，模型收敛；因此我们可以得到该模型中的参数估计值(表1)，这与我们从SAS和SPSS[7]得到的结果基本一致。

讨 论

本文利用Cox回归模型在生存分析中的优势，结合贝叶斯统计分析方法，构建基于贝叶斯条件下的Cox回归模型，通过其统计分析工具OpenBUGS软件[6]进行Gibbs抽样和马尔科夫迭代，实现对模型中参数的贝叶斯估计。一方面，克服了小样本资料在Cox回归模型中的限制[7]；另一方面，提高了在数据删失、不完全的状态下对研究对象生存影响因素估计的精度[5]。

贝叶斯统计分析方法是近几十年来发展起来的一种数理统计方法。随着其统计分析工具OpenBUGS软件[6]的不断更新和完善，贝叶斯统计分析方法日益受到重视并在各个领域得到广泛的应用[11-13]。基于贝叶斯统计框架下的Cox比例风险回归模型将待估计的参数作为随机变量而不是常数，并对其指定适当的先验信息，再结合该参数的样本信息和总体信息，得到参数的后验信息进而实现参数的贝叶斯估计[2]。但是，值得注意的是在利用贝叶斯统计分析方法进行推断时最重要的，也是最受经典统计学派批判的是先验信息的选择以及如何利用先验信息确定先验分布[2]。由于先验信息常常会受到主观因素的影响，尽管许多统计学家提出了多种方法，但至今理论上仍然没有一个统一的确定先验信息的方法。而本文对Cox回归模型中待估计参数指定的无信息正态先验分布，已经得到了多次验证[9,14]。除此之外，本文所采用的实例满足比例风险假定的要求[7]，因此可以利用其进行实证分析。

[1] Cox DR,Hinkly DV.Theoretical Statistics.New York:John Wiley &Sons.1974.

[2] 韦来生编著.贝叶斯统计.北京:高等教育出版社,2016，3.

[3] Jennifer Clarke,Mike West.Bayesian Weibull tree models for survival analysis of clinico-genomic data.Statistical Methodology,2008,5(3):238-262.

[4] Jaeyong Lee,Jinseog Kim,Sin-Ho Jung.Bayesian analysis of paired survival data using a bivariate exponential distribution.Lifetime Data Anal,2007,13(1):119-137.

[5] 林静.基于MCMC的贝叶斯生存分析理论及其在可靠性评估中的应用.南京:南京理工大学,2008.

[6] 张继巍,高文龙,李娟生，等.OpenBUGS软件介绍及应用.中国卫生统计,2017,34(1):170-172.

[7] 孙振球,徐勇勇主编.医学统计学.第4版.北京:人民卫生出版社,2014,291-294.

[8] 方积乾主编.卫生统计学.第7版.北京:人民卫生出版社,2012,420-422.

[9] Spiegelhalter D,Thomas A,Best N,et al.Open BUGS user manual (version 3.2.3).Cambridge:MRC Biostatistics Unit,2014.

[10] Congdon P.Applied Bayesian Modelling.England:John Wiley and Sons,2003.

[11] Lyle W,Konigsberg,Frankenberg.Bayes in Biological Anthropology.American Journal of Physical Anthropology,2013,152(57):153-184.

[12] Du Changde,Luo Ali,Yang Haifeng.Adaptive stellar spectral subclass classification based on Bayesian SVMs.New Astronomy,2017,51:51-58.

[13] Spence GT,Steinsaltz D,Fanshawe TR.A Bayesian approach to sequential meta-analysis.Statistic in Medicine,2016,35(29):5356-5375.

[14] 张尧庭,陈汉峰.贝叶斯统计推断.北京:科学出版社,1991.

教育部人文社科项目(15XJC910001)；兰州大学高校基本科研业务费(LZUjbky-2016-025)

†张继巍，高文龙为共同第一作者

△通信作者：李娟生，E-mail：lijsh@lzu.edu.cn

张 悦)