关于丢番图方程x3+1=413y2*
2021-04-27华程
华 程
(泰州学院 数理学院,江苏 泰州 225300)
1 引言
有许多学者研究过如下形式的丢番图方程:
x3+1=Dy2,D>0.
(1)
文献[1]证明了,当D>2无平方因子且不含6k+1型的素因子时,方程(1)只有平凡解(x,y)=(-1,0).但当D含6k+1型的素因子时,求方程的非平凡解十分困难,其中一类典型的不定方程为
x3+1=7qy2,q为奇素数.
(2)
对方程(2)的研究到目前只有一些零散的结果[2~7].本文讨论了q=59的情形,证明了如下定理:
定理1 不定方程
x3+1=413y2
(3)
只有平凡解(x,y)=(-1,0).
2 主要结果的证明
引理1[8]设p是奇素数,则方程4x4-py2=1除p=3,x=y=1和p=7,x=2,y=3外,无其他的正整数解.
引理2[8]方程x2-3y4=1仅有整数解(x,y)=(±2,±1),(±7,±2),(±1,±0).
引理3[8]设p是奇素数,则方程x4-py2=1除p=5,x=3,y=4和p=29,x=99,y=1820外,无其他的正整数解.
定理1的证明因为(x+1,x2-x+1)=1或3,故方程(3)可分为以下8种情形:
情形Ix+1=59u2,x2-x+1=7y2,y=uv,(u,v)=1;
情形IIx+1=7u2,x2-x+1=59y2,y=uv,(u,v)=1;
情形Ⅲx+1=u2,x2-x+1=413v2,y=uv,(u,v)=1;
情形Ⅳx+1=413u2,x2-x+1=v2,y=uv,(u,v)=1;
情形Ⅴx+1=177u2,x2-x+1=21v2,y=3uv,(u,v)=1;
情形Ⅵx+1=21u2,x2-x+1=177v2,y=3uv,(u,v)=1;
情形Ⅶx+1=3u2,x2-x+1=1239v2,y=3uv,(u,v)=1;
情形Ⅷx+1=1239u2,x2-x+1=3v2,y=3uv,(u,v)=1.
下面分别讨论.
情形Ⅰ由第一式得x=59u2-1,代入第二式,整理得
(118u2-3)2-7(2v)2=-3.
(4)
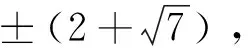
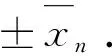
118u2-3=±xn.
(5)
容易验证下式成立:
xn+2=16xn+1-xn,x0=2,x1=37.
(6)
若n为偶数,则由(6)知xn是偶数,此时(4)不成立.若n为奇数,则由(6)知xn≡1(mod 3),此时(5)成为
u2=±1(mod 3).
(7)
由(7)知,只需考虑(5)中的118u2=xn+3,其中n为奇数.
对递归序列(6)取模5,得周期为6的剩余类序列:2,2,0,3,3,0,2,2,…,且当n≡3(mod 6)时,xn≡3(mod 5),此时有3u2≡1(mod 5),即(3u)2≡3(mod 5),但3是模5的平方非剩余,故排除,剩下n≡1,5(mod 6),即n≡1,5,7,11(mod 12).
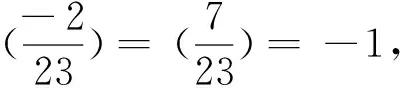
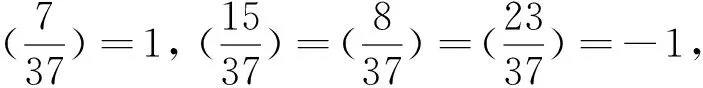
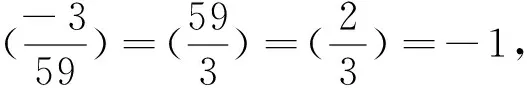
情形Ⅲ由第二式得(2x-1)2+3=413×4×v2=7×59×(2v)2,故(2x-1)2≡-3(mod 683),由情形Ⅱ知,不可能,故在该情形方程(3)无整数解.
情形Ⅳ解第二式得x=0,1,均不适合第一式,故在该情形方程(3)无整数解.
情形Ⅴ由第一式得x=177u2-1,代入第二式,整理得
(354u2-3)2-21(2v)2=-3.
(8)
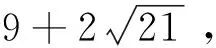
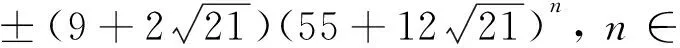
因此根据(8)有
354u2-3=±xn.
(9)
容易验证
xn+2=110xn+1-xn,x0=9,x1=999.
(10)
对递归序列(10)取模16,得剩余类序列的周期为2,且n≡0(mod 2)时xn≡9(mod 16),n≡1(mod 2)时xn≡7(mod 16).此时式(9)成为
354u2-3≡±9,±7(mod 16).
(11)
由式(11)得354u2≡12,-6,10,-4(mod 16) ,即2u2≡12,10(mod 16),也即u2≡6,5(mod 8),均为模8的平方非剩余, 故在该情形方程(3)无整数解.
情形Ⅵ由第二式得(2x-1)2+3=3×59×(2v)2,故(2x-1)2≡-3(mod 59),由情形Ⅱ知,不可能,所以在该情形方程(3)无整数解.
情形Ⅶ由第二式得(2x-1)2+3=21×59×(2v)2,故(2x-1)2≡-3(mod 59),由情形Ⅱ知,-3是模59的平方非剩余,所以在该情形方程(3)无整数解.
情形Ⅷ将第一式代入第二式,整理得(2v)2-3(826u2-1)2=1,故有
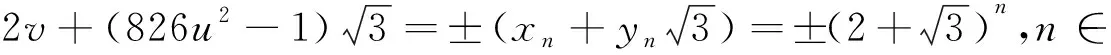
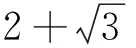
826u2=yn+1.
(12)
可验证:
xn+2=4xn+1-xn,x0=1,x1=2.
(13)
yn+2=4yn+1-yn,y0=0,y1=1.
(14)
xn+1=2xn+3yn,yn+1=xn+2yn.
(15)
x2n=xn2+3yn2,y2n=2xnyn,xn2-3yn2=1.
(16)
xn-1=2xn-3yn,yn-1=-xn+2yn.
(17)
若n≡0(mod 2),则由(14)知yn≡0(mod 2),此时式(12)不成立.
若n≡1(mod 4),令n=4k+1(k∈), 则由(15)、(16)可得
即
413u2=x2ky2k+1.
又因(x2k,y2k+1)=(x2k,x2k+2y2k)=(x2k,2y2k)=1,所以下列情形之一成立:
x2k=413m2,y2k+1=h2,u=mh,(m,h)=1.
(18)
x2k=m2,y2k+1=413h2,u=mh,(m,h)=1.
(19)
x2k=7m2,y2k+1=59h2,u=mh,(m,h)=1.
(20)
x2k=59m2,y2k+1=7h2,u=mh,(m,h)=1.
(21)
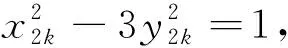
对于(20),由(15)得,y2k+1=x2k+2y2k,故有59h2=7m2+2y2k,即
59h2-7m2=2y2k.
(22)
因x2k和y2k+1均为奇数,故m和h均为奇数,从而m2≡h2≡1(mod 8).又y2k≡0,4(mod 8),故2y2k≡0(mod 8).对(22)两边取模8,得-4≡0(mod 8),不可能.
对于(21),由类似于式(20)的讨论知,它也不可能成立.
若n≡-1(mod 4),设n=4k-1(k∈),则由(15)、(16)、(17)式可得
2y2k(2x2k-3y2k)=2y2kx2k-1,
即413u2=x2k-1y2k.又因为(x2k-1,y2k)=(2x2k-3y2k,y2k)=(2x2k,y2k)=2,所以下列情形之一成立:
x2k-1=2m2,y2k=826h2,u=2mh,(m,h)=1.
(23)
x2k-1=826m2,y2k=2h2,u=2mh,(m,h)=1.
(24)
x2k-1=118m2,y2k=14h2,u=2mh,(m,h)=1.
(25)
x2k-1=14m2,y2k=118h2,u=2mh,(m,h)=1.
(26)
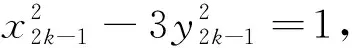
由(24)的第二式y2k=2h2得xkyk=h2,考虑到(xk,yk)=1,有xk=a2,yk=b2,故(a2)2-3b4=1,根据引理2知,a2=1,此时xk=1,从而k=0,所以(24)的第一式不成立.
由(25)的第二式得xkyk=7h2,考虑到(xk,yk)=1,有
xk=a2,yk=7b2,h=ab,(a,b)=1,
(27)
或
xk=7a2,yk=b2,h=ab,(a,b)=1.
(28)
若(27)成立,则有
a4-3(7b2)2=1.
(29)
由引理3知,方程(25)仅有整数解(a,b)=(±1,0),此时y2k=0,故k=0,所以(25)的第一式不成立.
若(28)成立,则有
(7a2)2-3b4=1.
(30)
由引理2可知方程(30)仅有整数解(a,b)=(±1,±2),所以xk=7,从而k=2.这时n=7,故由(12)可得826u2=y7+1=2912,不可能.
仿式(25)可证式(26)也不可能成立.
综上,在该情形时不定方程(3)无整数解.定理1得证.
