基于组合特征选择的目标识别算法研究

郑春红，王传聪，林稚璞，杨 刚

(西安电子科技大学 电子工程学院,陕西 西安 710071)

基于组合特征选择的目标识别算法研究

郑春红，王传聪，林稚璞，杨 刚

(西安电子科技大学 电子工程学院,陕西 西安 710071)

针对飞机遥感图像识别，对一种基于组合特征选择的目标识别算法进行了研究。考虑获取的飞机样本数量有限，且存在旋转、遮挡等现象，采用提取图像熵值、归一化转动变量、Fourier描述子、Hu矩和Zernike矩不同的不变矩描述其整体和细节特征，用离差标准化的归一化方法进行特征融合。考虑组合不变矩维数相对较高，用主成分分析(PCA)算法进行特征选择以避免维数灾难。用具参数优化的支持向量机(SVM)进行分类识别。给出了目标识别算法的流程。进行了手写数字和飞机目标识别两个仿真实验，结果表明：该特征选择方法在基于MNIST数据集的小样本手写体数字图像识别中，识别效果良好；在有限样本的飞机识别中，经特征选择后识别效果有较大改善，识别时间缩短，训练样本数据多，识别的精度会更高，但当飞机目标的不同姿态下形状发生变化时识别效果会变差。

遥感飞机图像； 目标识别； 组合不变矩； 特征选择； 主成分分析法； 支持向量机； 识别效果； 参数优化

0 引言

目标自动识别是机器视觉的一个重要研究方向，在航空、航天、医学和自动化等领域有广泛的应用前景。目前，在飞机目标识别领域，主要的方法是提取图像的不变矩进行组合。文献[1]提出将仿射矩和归一化转动变量(NMI)进行组合，用Fisher线性判别分类器实现飞机目标的识别。文献[2]提取飞机图像的Hu矩、仿射矩和归一化傅里叶描述子(NFD)三类不变量进行特征级融合，并结合支持向量机(SVM)实现飞机目标识别。文献[3]利用图像一阶直方图的颜色矩特征和由灰度共生矩阵生成的图像区域纹理特征，并采用聚类分析算法对飞机图像进行识别。文献[4]提出一种基于边缘形状特征的飞机目标识别算法，由粗到精地进行模板匹配，粗匹配过程负责定位飞机目标，精匹配过程利用主成分分析(PCA)和最近邻算法(KNN)完成目标的准确识别。文献[5]对上述方法进行改进，用圆投影特征进行粗匹配确定飞机目标，在精匹配阶段提取图像的Harris-Laplace角点、颜色不变矩和Zernike矩，并使用欧氏距离与样本图像进行加权匹配，最终实现飞机目标的识别。

上述方法都使用由多个不变性特征构成的高维组合不变性特征描述飞机目标，但由于组合不变性特征的维数较高，易产生“维数灾难”，且特征集中的冗余特征和不相关特征会降低识别效果，因此必须对组合不变性特征进行特征选择去除冗余特征和不相关特征。目前，在特征选择领域，主要的方法是利用分类器的识别结果作为评价函数选择最优特征子集。文献[6]将人工神经网络的识别结果作为评价函数，结合遗传算法进行特征选择。文献[7]组合了特征子集间的区分度和SVM的分类结果进行特征选择，取得了较好的效果。但这些方法选择出的特征通用性较弱，若改变分类器，还需重新进行特征选择。因此，本文用PCA方法根据特征集间的内部属性直接选择贡献度最优的特征子集实现特征选择。通过分析目标图像的结构特征，同时借鉴特征融合和特征选择的理念，提出了一种基于组合特征选择的目标识别方法。先提取飞机目标图像中图像的熵、归一化转动变量(NMI)、Hu矩、Zernike矩和Fourier描述子5类不变矩进行特征融合，再用PCA方法选择贡献度最优的特征子集，最后以SVM作为分类器实现目标识别。

1 组合特征描述

在飞机二值目标图像的特征提取过程中，既能反映形状又能描述局部细节的特征均是形状特征，而形状特征又分为整体描述特征和局部细节特征。针对飞机目标图像，本文选择提取图像的熵值、归一化转动变量、Fourier描述子、Hu矩和Zernike矩对目标进行描述。

1.1整体描述特征

图像的熵是一种特征的统计形式，它反映了图像中所含平均信息量的多少。在一幅二维图像中，图像的熵值常常是较稳定的，仅受图像内容复杂度的影响，因此适于将其作为一种描述整体分布的特征进行提取。由文献[8]，定义数字图像的熵为

(1)

式中：n=M×N为目标图像的大小；f(i，j)为点(i，j)处的像素值。

在物理学中，转动惯量是指刚体绕轴作旋转运动时的惯性，其量值取决于物体的形状、质量分布及转轴的位置。同理，计算图像的归一化转动变量(NMI)时，可将图像中每个像素视作是有质量的点，将每个点的灰度值看作此点的质量。因此，NMI的定义为

rNMI=

(2)

式中：(cx，cy)为图像灰度的质心，类似于物理学重心的概念[9]。因NMI特征具良好的缩放、旋转和平移不变性，且不同目标的NMI特征有明显差异，因此可用NMI特征对目标进行整体描述。

Fourier描述子是基于图像轮廓的不变量特征提取方法[10]。该法的要点是：假设图像中目标边界曲线上的点s(k)=[x(k)，y(k)]是以边界曲线周长为周期的函数，则此周期函数就可展开成傅里叶级数，并将傅里叶级数中的一系列系数称为Fourier描述子，其计算公式为

(3)

式中：u=0，1,2，…，N-1。然后以a(1)为基准将得到的Fourier描述子进行归一化，归一化后的Fourier描述子具尺度、旋转和平移的不变性。因整体形状的能量多集中于低频部分，故一般只使用归一化Fourier描述子的低频分量对目标形状的相似差异进行描述。

1.2细节描述特征

HU在1962年提出了Hu矩，并证明了Hu矩具旋转、缩放和平移不变性，且可较好地描述目标的形状细节[11]。Hu矩共由七个不变矩组成，分别为

M1=η20+η02

(4)

M2=(η20-η02)2+(3η21-η03)2

(5)

M3=(η30-3η12)2+(3η21-η03)2

(6)

M4=(η30+η12)2+(η21+η03)2

(7)

M5=(η30-3η12)(η30+η12)[(η30+η12)2+

3(η21+η03)2]+(3η21-η03)(η21+η03)×

[(3η30+η12)2-(η21+η03)2]

(8)

M6=(η20-η02)[(η30+η12)2-(η21+η03)2]+

4η11(η30+η12)(η21+η03)

(9)

M7=(3η21-η03)(η30+η12)[(η30+η12)2-

3(η21+η03)2]+(3η12-η30)(η21+η03)×

[(3η30+η12)2-(η21+η03)2]

(10)

式中：ηpq为归一化中心距，且

(11)

此处：μpq为图像的中心矩。离散化后图像的p+q阶中心距可表示为

(12)

其中：p，q=0，1，2，…。

Zernike矩是图像中的点在Zernike多项式中投影所得的一组完备正交集，可构成任意阶相互独立的多重Zernike矩特征描述图像的形状信息。由文献[12]，灰度图像中Zernike矩的定义为

(13)

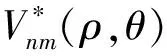
在获得的5类特征中，图像的熵、NMI和Fourier描述子可描述目标的整体形状特征；Hu矩和Zernike矩可描述图像的局部细节特征，因此需将这5类特征组成一个行向量进行处理。

1.3特征融合

因提取的特征结果中包含多类不变量，其中可能存在奇异样本数据，故需用数据归一化方法进行特征融合。本文采用离差标准化的归一化方法，这是一种对原始数据的线性变换，能使结果的值映射到区间[-1，1]中，可消除奇异数据对识别过程的影响，加快学习过程的收敛速度[2]。其具体步骤为，先设获得的组合特征向量x=[x1x2…xn]，再求取特征向量的最大值xmax和最小值xmin，最后用转换函数将特征映射到[-1，1]中。其中转换函数可表示为

(14)

2 特征选择

在上述的相关特征中，Fourier描述子序列取12维系数的模值作为特征，而Zernike矩取11阶系数 88个特征值，因此相关的整体特征和局部特征总共109个。在这些数据中不可避免会出现冗余现象，因此需采用特征选择去除冗余，避免“维数灾难”。

PCA算法是目前应用广泛的特征选择方法，主要通过对特征集的协方差矩阵进行分析，选取对方差贡献最大的特征子集，实现在降低特征维度的同时保留最大特征信息[13]。即在信息损失最小的情况下，通过将原多个指标转为一个或几个主成分，解决数据空间维数过高的瓶颈问题。

该算法的主要步骤如下：设从训样本集中提取得到的特征集为Xm×n={X1，X2，…，Xn}。此处：n为每个样本的特征数；m为训练样本数；Xl×n为测试样本集的特征集(l为总的测试样本数)。

a)计算训练样本特征集Xm×n的协方差矩阵Sn×n。

b)计算Sn×n的特征值和特征向量矩阵Cn×n，并将特征值按从大到小的顺序排列，λ1>λ2>…>λn。

c)计算累计贡献率。根据选定的贡献率，选取对应的Cn×n的前列，构成Cn×p。

d)计算训练样本集样本的主成分Xm×p=Xm×nCn×p和测试样本集的主成分Xl×p=Xl×nCn×p。

在特征选择阶段，选择保留累计贡献率超过99%的主成分。因此，对提取获得的特征用PCA算法进行特征选择后，保留前50个主成分即可，能在保留最大信息量的前提下，将特征维数从109维降低至50维。

3 支持向量机

SVM最初于20世纪90年代由VAPINK提出，是一种基于结构风险最小化原则进行参数训练的神经网络分类技术，具有出色的小样本学习性能和良好的泛化性能，可根据有限样本信息在模型的复杂度和学习能力之间寻求最佳的折中，以取得最好的推广能力[14]。

SVM的要点是将非线性可分的数据通过一个核函数φ：RN→F映射到线性可分的特征空间F，再通过解约束优化问题：

从而构造出最优超平面

H:f(x)=ωTφ(x)+b

式中：ω，b为分类超平面的参数；ξ为松弛变量；C为对分类误差的惩罚因子。因此，在SVM中，首先需考虑C，φ的选择。

3.1核函数选择

SVM中有多种核函数，选择不同的核函数得到的结果也不同。目前较常用的核函数有线性核、多项式核、径向基核函数(RBF核)和Sigmoid核等，本文选用超参数较小，但性能优异的RBF核函数：K(xi，yi)=exp(-γ|xi-xj|2)。此处：γ为和函数的参数，且γ>0；xj为核函数的中心。

3.2寻找最优参数对(C，γ)

在SVM中，C的作用是在确定的特征空间中调节学习分类器的置信范围和经验风险比例以增强推广能力，C选择合适的值会提升分类效果。在RBF核函数中，γ为核参数，可改变映射函数，进而影响样本特征子空间分布的复杂程度。

由于SVM的参数(如C,γ)对训练时间和识别结果的影响非常大，因此需选取最优参数对(C，γ)。本文通过k折交叉验证法进行网格寻优搜索实现参数的选取，具体步骤为：先固定参数对(C，γ)取值范围，并为(C，γ)取值，然后将已有样本集分为k个子集，将每个子集均作一次测试集，剩余的k-1个作为训练集，交叉验证重复k次，每次在测试集上对训练集中得到的模型进行测试得到分类准确率，并将k次的平均交叉验证分类准确率作为分类器在参数对(C，γ)时的性能指标，最后在取值范围内调整参数对(C，γ)的值，重复交叉验证过程，多次循环上述过程直至得到最佳交叉验证率，同时得到最佳参数对(C，γ)。

4 实验结果与仿真

在实验中，首先将样本集随机划分为训练样本集和测试样本集，再提取训练本集中图像的熵、NMI、Hu矩、Fourier描述子和Zernike矩五种特征，并用归一化方法进行特征融合后组成图像的组合不变性特征，随后再用PCA算法对组合不变性特征进行特征选择，将特征维度减少至50维，用选择后的特征集训练参数优化的SVM分类器，得到用于飞机目标识别的分类器模型；最后提取测试样本集的组合不变性特征并进行特征选择，输入SVM分类器进行分类，得到最终的测试结果。整体的目标识别流程如图1所示，分别对手写体数字和飞机目标进行仿真实验验证。

4.1手写数字识别

MNIST数据集是一个手写数字库，包含训练数据60 000条和测试数据10 000条，每幅图像大小为28像素×28像素，且均为灰度图像，实验数据集由MNIST数据集中的图片随机旋转任意角度构成，且从MNIST数据集的训练数据和测试数据中随机抽取一定量的数据组成新的数据集10个用于测试，新组成的数据集分别包含训练数据600，1 200，1 800，…，6 000条和测试数据100，200，300，…，1 000条。MNIST数据集中手写数字的样例如图2(a)所示，实验数据集样例如图2(b)所示。

在新生成的10个数据集中，分别用SVM识别方法和基于组合特征选择方法的目标识别系统对旋转的手写数字进行测试，所得结果如图3所示。由图3可知：本文方法的识别率高于经典SVM识别方法，特别是当样本数量较少时识别效果更好。

4.2飞机目标识别

在实验中，共收集到8类飞机遥感图像，包括A-10、B-1B、B-52、F-14、F-111、Mirage-2000、Mirage-F1和SAAB-37型号的军用飞机，每类88幅，图像共704幅，且每幅为128×128的灰度图像。从每类飞机图像中随机选择38幅作为训练图像，剩余的50幅作为测试图像，共得训练数据304条和测试数据400条。在实验数据集中，不仅包括了旋转不同角度的飞机图像，而且包括部分位置被遮挡的遥感飞机图像，用于对算法的鲁棒性进行检验。所得旋转不同角度的飞机遥感图像如图4(a)～(c)所示，尾部被遮挡的飞机遥感图像如图4(d)所示。

为测试特征选择对识别性能的影响，同时验证训练样本数量对识别能力的影响，从每类飞机图像的训练集中随机选取10，15，20，25,35幅图像分别作为训练样本集，而使用测试集中的所有图像作为测试样本集，然后分别用具特征选择和不具特征选择的目标识别系统进行测试，运行100次后得到的平均识别率结果和平均运行时间图5所示。其中：运行时间为对训练样本集(样本数×8)和测试集(50×8)进行分类识别所需的总时间。

由图5可知：提取的组合不变矩可获得较好的识别效果，而且经过特征选择后，识别效果和所需时间有较大改善。同时可发现：飞机目标的分类识别时，训练样本数据多，识别的精度会更高，但时间消耗也更多。

5 结束语

本文对飞机遥感图像的分类识别进行了研究，提出了一种基于组合不变矩及特征选择的SVM目标识别算法，实现了对飞机目标的高精度识别。仿真实验结果表明：针对样本数较少且旋转、遮挡的飞机目标进行识别时，该方法可消除目标的旋转、遮挡对识别结果的影响，其识别效果优于不采用特征选择方法；随着样本数的增加，平均识别率可提升到99%。旋转后手写数字数据集MNIST的实验结果表明：在训练样本数较少时该方法仍有较高的识别精度和速度，能在背景简单的目标识别时取得较好的效果，因此可用于多种目标识别领域。此外，本文的方法主要使用组合不变矩特征对目标的形状进行描述，当飞机目标的不同姿态下形状发生变化时识别效果将会下降，因此寻找或构建新的特征使其对目标进行更好的描述是提升识别算法性能的关键。

[1] 曾万梅， 吴庆宪， 姜长生． 基于组合不变矩特征的空中目标识别方法 [J]． 电光与控制， 2009, 16(7): 21-24.

[2] 朱旭峰， 马彩文， 刘波. 基于特征级融合和支持向量机的飞机识别[J]. 光电子·激光， 2011, 11(22): 1710-1713.

[3] 吴东华, 夏洪山, 徐波. 基于混合矩特征提取的飞机图像识别[J]. 微电子学与计算机, 2011, 10(28): 188-193.

[4] LIU G, SUN X, FU K, et al. Aircraft recognition in high-resolution satellite images using coarse-to-fine shape prior[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(3): 573-577.

[5] 曾接贤, 付俊, 符祥. 特征点和不变矩结合的遥感图像飞机目标识别[J]. 中国图象图形学报, 2014, 19(4): 592-602.

[6] LI L, WEINBERG C R, DARDEN T A, et al. Gene selection for sample classification based on gene expression data: study of sensitivity to choice of parameters of the GA/KNN method[J]. Bioinformatics, 2001, 17(12): 1131.

[7] 谢娟英, 谢维信. 基于特征子集区分度与支持向量机的特征选择算法[J]. 计算机学报, 2014, 37(8): 1704-1718.

[8] ZHANG S J, JING Z L. A novel translation,scale and rotation invariant feature extractor and its applications to target recognition[J]. Machine Learning and Cybernetics, IEEE, 2004, 6: 3678-3683.

[9] 门蓬涛, 张秀彬, 张峰, 等. 基于NMI特征的目标识别与跟踪[J]. 微计算机信息, 2004, 20(3): 24-26.

[10] JIA H T, XIE M. Improvement of Fourier descriptor using spatial normalization[J]. ISCIT IEEE, 2005(2): 1 284-1287.

[11] HU M K. Visual pattern recognition by moment invariants[J]. IRE Transactions on Information Theory, 1962(8): 179-187.

[12] ARVACHEH E M, TIZHOOSH H R. Pattern analysis using Zernike moments[C]∥ IEEE Instrumentationand Measurement Technology Conference Proceedings. [S. l.]: IEEE, 2005: 1574-1578.

[13] JOLLIFFE I. Principal component analysis[M]. New York: Springer-Verlag, 1986: 10-28.

[14] CONES C, VAPNIK V. Support vector networks[J]. Machine Learning, 1995, 20: 273-297.

TargetRecognitionAlgorithmResearchBasedonCombinedFeatureSelection

ZHENG Chun-hong， WANG Chuan-cong， LIN Zhi-pu， YANG Gang

(School of Electronic Engineering, Xidian University, Xi’an 710071, Shaanxi, China)

For remote sensing aircraft image recognition problem, a target recognition algorithm based on combined feature selection was studied in this paper. With the consideration of limited aircraft samples and rotated, occluded aircraft images, the global and local features were described using invariant moments of picture enteropy, normalized rotation variable, Fourier describer, Hu moment and Zernike moment. The feature mergence was realized by dispersion standardization of normalized method. As combined invariant moments dimension was relatively high, principal component analysis (PCA) algorithm was used for feature selection, which could avoid dimensionality curse. The aircraft classification was implemented by support vector machine (SVM) with parameter optimization. The flowchart of the target recognition algorithm was given. The two recognition samples of handwriting digital and aircraft were simulated. The results show that the recognition effect of the handwriting digital in MNIST database is good, and the recognition effect has been improved and the recognition time is shorten after feature selection for aircraft with the limited samples. The more samples training, the higher recognition accuracy. But the recognition effect will become worse when the aircraft shape has changed under different attitude.

aircraft image; target recognition; combined invariant moment; feature selection; principal component analysis (PCA); support vector machine (SVM); recognition effect; parameter optimization

1006-1630(2017)05-0059-06

2016-10-21;

2017-05-09

上海航天创新基金资助(SAST201453)

郑春红(1969—)，女，副教授，主要研究方向为智能信息处理、机电一体化等。

TP391.41

A

10.19328/j.cnki.1006-1630.2017.05.009