本征正交分解在翼型气动优化中的应用研究

李 波，龚春林，粟 华，谷良贤

(西北工业大学 航天学院 空天飞行技术研究所,陕西 西安 710072)

本征正交分解在翼型气动优化中的应用研究

李 波，龚春林，粟 华，谷良贤

(西北工业大学 航天学院 空天飞行技术研究所,陕西 西安 710072)

为降低机翼翼型气动优化的仿真代价，提出了一种基于本征正交分解(POD)的翼型自适应快速优化方法。建立气动流场数据的代理模型以预测流场。为简化求解规模和难度，采用POD代理模型优化。为进一步提高精度，提出了基于序贯POD代理模型自适应优化，在优化过程中实时更新POD基，即在优化中间结果的基础上重新采样，以更新POD空间，基于动态数据库构建代理模型。给出了不同优化方法的求解流程。以NACA0012翼型为例分别对直接翼型优化、基于代理模型的翼型优化和基于POD代理模型的翼型优化方法进行了对比分析。结果表明：与直接优化方法相比，基于POD代理模型的翼型优化能显著提升优化效率，且拟合精度更高。

翼型设计； 气动优化； 模型降阶； 本征正交分解(POD)； 代理模型； 基于序贯POD代理模型； 优化效率； 拟合精度

0 引言

改善飞行器的升阻力特性一直是飞行器设计追求的重要指标。气动优化涉及大量的气动分析，存在计算周期长、数据处理繁琐的不足。基于代理模型的气动优化是提高效率最有效的方法之一，在气动优化中获得了大量应用[1]。文献[2]将动网格引入翼型设计优化，用自编程序实现动网格生成，通过集成商业软件Pointwise，CFD计算软件Fluent 完成边界条件生成和流场解算节省大量的重复性操作；文献[3]建立了升力系数和阻力系数的Kriging自适应代理模型与支持向量回归自适应代理模型，明显提高了气动分析的计算效率；文献[4]综合Kriging代理模型和遗传算法进行了低雷诺数翼型的气动外形正优化设计。但在流体分析阶段，直接基于流体计算软件的优化过程的时间代价很大；代理模型只能建立计算状态、几何参数与升力系数、阻力系数等气动标量数据间的关系，丢弃了流场中大量的气动特征，如压强系数、摩擦因数等场量分布数据，构建的近似模型实际上已失去了描述完整流场的能力，而这些场量数据恰是构成升阻力等气动评价指标的关键，这必然会降低评价指标的拟合精度。

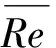
通常，应用POD代理模型需要提前获取一定数据的流场信息，即需已知流场的部分采样解。原实际物理模型信息可通过系统的若干已知试验解(或数值解)提取得到，或通过大量的仿真数据获取。基于POD的气动优化流程能尽可能全面地利用原气动数据特性以提高拟合精度。本文将POD方法引入翼型气动优化，建立气动流场数据的代理模型，对流场进行预测；提出基于POD代理模型的自适应序贯优化设计流程，在优化过程中动态修正POD代理模型拟合精度，从而弥补单次POD代理模型构建过程中的误差，以获得更高的拟合效果。用一个二维翼型设计优化对本文方法的有效性进行验证分析。

1 本征正交分解

POD方法中的本征模态是按对应本征值所含流场能量大小进行排序的，通过捕捉高能量本征模态能较好地描述和分析随机场的特性。

1.1POD基本理论

POD方法的一个重要特点就是可将相干结构及其包含的能量联系起来，即从能量的角度对场量进行分析，并识别流场中含最大能量的模态[13]。POD方法的核心是寻找函数或场量空间{vn(x)∈Ω}的一组“最优”正交基{φ1,φ2,φ3,…,φn}。假设vn(x)可由若干正交基近似，则vn(x)可用这组“最优”正交基{φ1,φ2,φ3,…,φn}近似表示，即

(1)

式中：φi(x)为vn(x)的特征函数或基函数；ηi为φi(x)的相关系数；n为基函数选取的数量。为求解φi(x)，需知道vn(x)中的部分样本点。

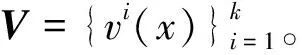
(2)

式中：〈 〉为内积运算符。

用Lagrange乘子法将约束问题式(2)转为无约束问题，再用变分法来处理。

定义

K(x,x′)=〈vn(x),vn(x′)〉

(3)

则基函数φi(x)须满足

(4)

式中：K(x,x′)为核函数，是半正定的自关联矩阵。优化问题式(2)转为式(4)中求解核函数K的特征向量和特征值，即可得到最优值。

实际情况下核函数的规模很大，直接求解较难。因此，用文献[14]提出的快照技术求解。该法的要点是将原函数空间元素vn(x)用φi(x)的线性组合进行近似处理，能一定程度减少计算内存消耗。

1.2POD计算流程

具体实现过程如下。

V=[V(1)V(2)…V(k)]T=

(5)

(6)

式中：ai为特征值的特征函数。将式(6)代入式(4)，与φ的展开式比较可得

GGTA=λA

(7)

此时将式(2)的最优化问题转换为求GGT的特征值λ。

c)用奇异值分解法求解，G的奇异值可分解为

(8)

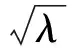
d)所得的ϑ的维数仍很高，需根据能量信息容量选择前t阶模态近似整个数据空间[15]。t应当尽量小，减小特征向量空间的规模，但应尽可能更精确地逼近原数据空间。t的选取可用以下方式确定，则有

(9)

式中：I(t)为能量信息容量或能量，I(t)越接近1，表明特征向量空间包含的原信息越完整，越接近原函数空间，通常认为I(t)大于95%即可；λi为Σ中对角线上按降维排列的特征值。一般情况下，特征值的大小以指数律下降，故只需较少的模态数即可实现对原数据空间的有效逼近。

e)基函数对应的系数可表示为

(10)

f)POD模型可表示为

(11)

2 基于POD代理模型优化设计

当t确定后，vn(x)可直接用系数η表示，用式(11)即可直接求出。此时，原vn(x)转换为t维η与φi(x)间的关系。通常η的维数仍较大，且不具直观物理意义。因此，实际使用时需建立η的代理模型，以进一步将其表示为场量对应状态变量的函数。

2.1POD代理模型优化

在长耗时和大量数据数值仿真或数值计算中，常用代理模型进行简化求解规模和难度。对如RSM，Kriging，RBF等传统代理模型，建立的代理模型时通常简化为标量处理，有

(12)

式中：“∧”表示代理模型输出[16-18]。

但当Y为场量时，需分别对每个数据点构建代理模型，代理模型则会花费极大的计算资源。且未考虑这些数据点间的联系，代理模型的精度也会有损失。

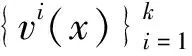
(13)

2.2优化流程

对场量构建POD代理模型，将整个优化问题用POD代理模型近似，提出基于POD代理模型优化设计流程。此时整个优化问题的设计变量变为POD代理模型基函数系数η。

2.2.1 代理模型优化流程

不同方法优化流程如图1所示。

由图1可知：在优化过程中，传统代理模型和POD代理模型都摒弃了优化代价巨大的分析计算过程，由代理模型近似，提高了计算效率；与传统代理模型相比，POD代理模型充分考虑数据间的关系，省去了对每个数据点都构建代理模型的过程，进一步提高了效率。POD代理模型优化步骤如下：

a)初始化优化问题；

c)计算POD代理模型基函数系数η；

d)基于POD代理模型得到近似输出；

e)判断是否收敛，是，退出；否，返回步骤d)。

2.2.2 序贯优化流程

整个优化流程的判断条件变为POD模型精度，每次优化结束后，若POD模型的精度不满足设计要求，则将当前最优结果加入POD数据库中重构代理模型，直至满足POD模型精度要求为止。

3 二维翼型气动优化

将本文基于序贯POD代理模型自适应优化求解方法用于二维翼型的设计优化。

3.1二维翼型气动优化模型

3.1.1 优化问题

以NACA0012经典翼型测试本文提出的序贯

POD代理模型自适应优化求解方法。令设计状态为：Ma=0.2，ρ=1.225 kg/m3，α=2.27°，Re=4.66×106。优化问题为最大化翼型升阻比Cl/Cd，同时保证阻力系数Cd小于基准翼型。优化问题数学形式可表示为

(14)

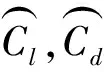
3.1.2 翼型采样

用CST参数化方法描述翼型截面信息与CST参数间的关系[19]。分别用5个设计变量描述二维翼型的上、下表面，其中包括2个形函数控制因子和3个Bernstein多项式权重控制因子bi。有

(15)

(16)

3.1.3 气动分析

用xfoil软件对翼型气动进行分析[20]。该软件是针对低雷诺数条件下翼型的数值模拟而专门开发的流场求解的开源程序，是国外用于低雷诺数翼型计算的主要工具，其准确性和可靠性在多篇文献中得到了验证。

3.1.4 优化算法

优化采用梯度算法(SNOPT算法)。SNOPT适于大规模、二次和非线性规划。在气动分析中，数据的维数和规模通常均是超线性的，故本文选择基于梯度的SNOPT非线性规划方法进行优化。

3.1.5 实验设计

数据库样本点采样用拉丁超立方(LHS)实验设计方法。LHS实验设计方法每个因子的水平等于点数，并进行随机组合，有能力拟合二阶或更非线性的关系。本文在设计初期，采用LHS在设计空间内抽取样本点100个，用xfoil软件进行翼型气动分析，生成各采样翼型流场解空间，用于构建POD代理模型和RBF代理模型。

本文使用的计算工具配置为：主频2.1 GHz的Intel双核处理器，内存4 GB；在vs2010平台上，采用C++自编程序计算。

3.2POD模型精度分析

在优化过程中，POD代理模型的误差会对最终优化结果精度产生影响。因此，在优化前，对POD代理模型的精度进行分析，折中求解计算过程中模型拟合精度和计算代价。

不同基函数阶数t时的POD代理模型构建时间和能量信息容量见表1。由表1可知：t=3时模型精度已高于95%，表明当前代理模型构建时所用数据库中的样本点数已足够；在POD模型拟合精度随t增加的同时，构建代价也随之增加。最终t=19时，POD代理模型的拟合误差达到0.01%，但其构建代价也最大。因此，在优化过程中需平衡模型精度与效率。POD代理模型的构建虽然花费时间长，但与CFD等高时耗的计算相比，几乎可忽略不计，本文在后续优化过程中取t=19进行分析计算。

表1 POD代理模型能量信息容量和构建时间

3.3二维翼型气动优化求解

分别对直接翼型优化、基于代理模型的翼型优化和基于POD代理模型的翼型优化方法进行分析。直接翼型优化，即建立基于xfoil的直接优化方法，每步优化气动分析用xfoil软件直接计算；基于代理模型的翼型优化，用RBF代理模型近似得到翼型的升阻比。

3.3.1 优化结果

将POD代理模型和RBF代理模型的优化结果生成的翼型代入xfoil软件计算分析，验证模型精度。不同优化方法气动优化结果见表2。由表2可知：与基准翼型NACA0012的升阻比44.4112相比，均有大幅提升，其中基于POD代理模型的提升较另两种方法更显著。表1中的误差为不同方法优化结果与xfoil验证计算结果的对比误差，优化时间仅为优化过程开始至优化迭代结束的时间，不包含代理模型构建时间。

表2 不同优化方法气动优化结果

自适应POD代理模型优化过程中，对POD代理模型进行11次重构能达到POD代理模型精度设计要求0.01%。序贯优化过程中，在每步优化迭代过程中，由于式(11)的维度较大导致优化变量增加，从而导致优化效率降低；代理模型每更新一次代理模型数据库，整个POD模型将重构一次，一定程度上增加了整个过程的计算代价，但提升了优化结果的精度；整个POD代理模型序贯优化的时间较直接基于xfoil软件的优化过程大幅减少，优化效率明显提升；但与RBF代理模型相比，POD代理模型序贯优化的效率有所降低，降低优化效率的同时增加了优化过程和结果的拟合精度。

3.3.2 结果分析

不同方法最后优化结果生成的翼型与基础翼型NACA0012如图3所示。由图3可知：三种方法的优化结果均是增加翼型上表面的厚度、减小下表面的厚度，以及改变基准翼型的弯度增加升阻比。图3中：c为弦长。

POD代理模型序贯优化结果代入xfoil软件中计算所得的翼型表面压强系数分布如图4所示。由图4可知：在整个翼型截面分布中，除前缘部分的误差较大外，其余部分的拟合精度均较高。前缘部分即在翼型头部的误差因翼型头部的压强分布梯度变化较大，代理模型难以精确拟合，而有翼型节点在前缘分布相对较少也是拟合精度降低的原因。

三种方法目标函数升阻比系数的迭代收敛结果如图5所示。由于本文使用基于梯度的优化算法SNOPT，导致不同方法在迭代过程中均出现了一定程度的振荡，但整个优化过程中收敛趋势仍很明显。

4 结论

本文提出了一种基于POD代理模型的高效自适应序贯优化方法，可为场量数据的拟合或优化提供一个有效的解决方法，不仅仅局限于气动场量数据。用二维翼型设计优化进行了比较分析，结果发现：第一，对比分析了基于直接法、POD代理模型和RBF模型的翼型优化方法，基于POD代理模型的翼型优化相比于直接优化方法能显著提升优化效率，且较代理模型有更高的拟合精度。第二，用基于动态数据库POD代理模型的自适应优化模型提升模型构建精度，但此过程会增加优化代价，降低优化效率；与CFD等高时耗的计算相比，整个过程计算量已很小。第三，POD代理模型构建需已知一定的采样解空间；因此，在构建POD代理模型前，需已有一定的采样解以便构建POD代理模型；如已有大量的工程试验数据，将其构建为POD代理模型进行优化可很大程度提升优化效率。随着对气动优化要求的提高，本文所用的评价指标升阻比并不能完全描述飞行器的气动性能，后续研究应加入更多有实际意义的评价指标和约束。

[1] 段焰辉, 蔡晋生, 刘秋洪. 基于代理模型方法的翼型优化设计[J]. 航空学报, 2011, 32(4): 617-627.

[2] 朱雄峰, 郭正, 侯中喜, 等. 基于动网格的翼型设计优化[J]. 国防科技大学学报, 2013, 35(2): 1-6.

[3] 夏露, 王丹, 张阳, 等. 基于自适应代理模型的气动优化方法[J]. 空气动力学学报, 2016, 34(4): 433-440.

[4] 陈学孔, 郭正, 易凡, 等. 低雷诺数翼型的气动外形优化设计[J]. 空气动力学学报, 2014, 32(3): 300-307.

[5] SIROVICH L. Turbulence and the dynamics of coherent structures[J]. Quarterly of Applied Mathematics, 1987, 45(3): 561-571.

[6] 杜娟. 流体力学方程基于POD方法的降维数值解法研究[D]. 北京: 北京交通大学, 2011.

[7] FRENO B, BRENNER T, CIZMAS P. Proper orthogonal decomposition applied to the Reynolds-averaged Navier-Stokes equations: AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition[C]∥ AIAA, 2013.

[8] TAN B T, DAMODARAN M, WILLCOX K E. Aerodynamic data reconstruction and inverse design using proper orthogonal decomposition[J].AIAA Journal, 2004, 42(8): 1505-1516.

[9] EVERSON R, SIROVICH L. The Karhunen-Loeve procedure for Gappy data[J]. Journal of the Optical Society of American, 1998, 12(8): 1657-1664.

[10] 白俊强, 邱亚松, 华俊. 改进型Gappy POD翼型反设计方法[J]. 航空学报, 2013, 34(4): 762-771.

[11] 王迅, 蔡晋生, 屈崑, 等. 基于改进CST参数化方法和转捩模型的翼型优化设计[J]. 航空学报, 2015, 36(2): 449-461.

[12] 曹长强， 蔡晋生， 段焰辉. 超声速翼型气动优化设计[J]. 航空学报, 2015, 36(2): 3774-3784.

[13] JOHANSSON P B V. Analysis of large data sets using proper orthogonal decomposition[R]. AIAA, 2006-3299, 2006.

[14] EVERSON R, SERVICE L. Karhunen-Loeve procedure for Gappy data[J]. J Opt Soc Am, 1995, 12(8): 1657-1664.

[15] BERKOOZ G, HOLMES P, LUMLEY J L. The proper orthogonal decomposition in analysis of turbulent flows[J]. Annual Review of Fluid Mechanics. 1993, 25: 539-575.

[16] MYERS R H, MONTGOMERY D C. Response surface methodology: process and product optimization using designed experiments[M]. New York: Wiley, 1995.

[17] SACKS J, WELCH W J, MITCHELL T J, et al. Design and analysis of computer experiments[J]. Statistical Science, 1989, 4(4): 409-423.

[18] HARDY R L. Multiquadratic equations of topography and other irregular surface[J]. Journal of Gelhysics Research, 1971, 76(8): 1905-1915.

[19] KULFAN B, BUSSOLETTI J. “Fundamental" parametric geometry representations for aircraft component shapes[C]∥ AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. [S. l.], AIAA, 2013: 1-45.

[20] DRELA M. XFOIL: an analysis and design system for low reynolds number airfoils[C]∥ Conference on Low Reynolds Number Airfoil Aerodynamics. Notre Dame: University of Notre Dame, 1989: 1-12.

ResearchandApplicationonProperOrthogonalDecompositioninAerodynamicOptimizationofAirfoil

LI Bo， GONG Chun-lin， SU Hua， GU Liang-xian

(Institute of Spaceplanes and Hypersonic Technologies, School of Astronautics, Northwestern Polytechnic University, Xi’an 710072, Shaanxi, China)

In order to reduce the simulation cost, an adaptive rapid optimization method based on proper orthogonal decomposition (POD) was proposed in this paper. The surrogate model of aerodynamic flow field data was established to predict the flow field. To simplify the solving and difficulty, POD surrogate model was adopted. To improve the accuracy more, based sequential POD surrogate model was used for adoptive optimal, which would renew POD basis in real time in the optimization process. It meant that the sampling was carried on again to renew POP space based on the intermediate results. The surrogate model was constructed based on dynamic data base. The influence of the POD surrogate model on the direct wing optimization, approximate model optimization and airfoil optimization based on POD surrogate model were compared and analyzed with NACA0012 airfoil as an example. The results showed that the airfoil optimization based on the POD surrogate model could improve the optimization efficiency significantly compared with the direct optimization method, and had higher fitting accuracy than the surrogate model.

airfoil design; aerodynamic optimization; reduced order model; proper orthogonal decomposition(POD); surrogate model; sequential based POD surrogate model; optimal efficiency; fixing accuracy

1006-1630(2017)05-0117-07

2016-12-29；

2017-02-27

国家自然科学基金资助(51505385)；上海航天科技创新基金资助(SAST2015010)

李 波(1992—)，男，硕士生，主要研究方向为多学科设计优化。

粟 华(1985—)，男，讲师，主要从事飞行器总体设计、多学科设计优化研究。

V211.412

A

10.19328/j.cnki.1006-1630.2017.05.019