基于数值实验的航行体流体动力参数研究

李 杰，李小林，傅惠萍

(1.上海交通大学 船舶海洋与建筑工程学院,上海 200240； 2.上海机电工程研究所,上海 201109)

基于数值实验的航行体流体动力参数研究

李 杰1，李小林2，傅惠萍1

(1.上海交通大学 船舶海洋与建筑工程学院,上海 200240； 2.上海机电工程研究所,上海 201109)

基于数值实验对用于航行体轨迹预报的航行体附加质量、位置导数及旋转导数等重要流体动力参数进行了研究。提出了基于物体摇荡运动的附加质量确定方法，根据傅里叶分析，给出了物体受到的附加质量力的分离方法和附加质量的计算方法；水动力数据是用CFD软件模拟物体周期摇荡运动的流场而得。基于上述方法，提出了基于运动状态突变流场模拟的附加质量和旋转导数计算方法。用两种方法分别计算了圆球和椭球的附加质量，两种方法的计算结果与势流理论结果一致。对细长水下航行体的旋转导数进行了计算，结果发现：头、尾附近的两个连接面对升力、力矩变化的贡献最大；两连接面及附近两单元面对应的升力旋转导数为负值；中间其他各面对应的升力旋转导数为正值。对细长圆柱体，改变头尾部形状可引起旋转导数的较大改变。用所提方法不仅可得到细长航行体包括附加质量和旋转导数的多种流体动力参数，而且能获得流体动力参数的空间分布特征。相较而言, 基于运动状态突变流场模拟的流体动力参数计算方法更为简便，且更便于分析流体动力的分布特性。

航行体； 流体动力； 附加质量； 旋转导数； 数值实验； 摇荡运动； 运动状态突变； 圆球

0 引言

物体流体动力参数一直是流体力学研究的主要对象。在基于试验、理论或数值的研究中，流体动力参数的研究往往是流体力学的研究基础。附件质量、位置导数和旋转导数等流体动力参数是航行体轨迹预报的重要参数[1]。采用势流方法可得物体附加质量的理论解，但该法仅限于规则外形物体。对复杂外形或受边界影响的非无界区域工况下流体动力参数研究常需要依赖于大量的模型实验研究，而基于物体摇荡运动测量附加质量是较成熟的试验方法[2-7]。一般情况下，实验研究结果能满足工程需要，但须投入较多人力、物力，而且实验结果较难体现流体动力参数的分布特征。随着数值模拟技术的发展，物体运动流场求解方法日益成熟，通过数值试验获得包括旋转导数的流体动力参数的方法已取得了丰富的研究成果[8-11]。这些方法往往是基于物理实验流场的再现，过程较复杂，计算周期较长。数值模拟具强可控性，可获得丰富的流场信息，利于细致地研究流体动力特性。开展基于流场数值模拟的流体动力参数研究有广泛的工程需求和较重要的理论意义。

本文对基于数值实验的航行体流体动力学参数进行了研究，给出了基于物体摇荡运动数值实验确定附加质量的方法，根据物体变速运动流体动力的变化规律，提出了相对更简便的基于运动状态突变流场模拟的附加质量和旋转导数计算方法。本文方法的所有流场的数值模拟基于商用软件Fluent完成，其过程更简洁，只要经过短期的非定常流场的模拟就可获得相应的流体动力参数，且易得到流体动力参数的空间分布，便于研究流体动力特性。

1 流体动力参数的数值研究方法

1.1基于摇荡运动的附加质量数值计算方法

设物体在均匀来流中作强迫摇荡运动，v为来流的速度，vi为摇荡运动的脉动速度，i=1～6。此处，假定来流速度与脉动速度满足关系

(1)

式中：L为物体的特征长度。摇荡运动遵循正弦规律

vi=voisin(ωit)

(2)

式中：ωi为摇荡的圆频率；voi为各方向速度脉动幅值(包括角速度)。

通过流场监控，得到物体所受到的力(力矩)为Fj(t)。 根据附加质量的概念，有

(3)

参照物理实验的处理方法，可通过对物体受到的流体作用力进行傅里叶分析获得附加质量。则

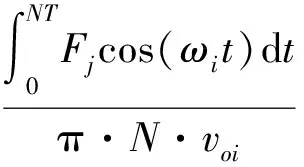
(4)

式中：T为摇荡运动对应的周期；N为周期数。

1.2基于运动状态突变流场模拟的附加质量和旋转导数计算方法

物体所受的流体动力与其所处的位置、姿态、运动速度和加速度等均相关。当其中的某些运动状态参数突然发生变化时，其受力也会出现相应的跳跃式变化。通过对物体运动状态突变流场的模拟，并监控比较受力的变化可获得相应的流体动力参数。

1.2.1 附加质量

当来流速度为v时，原静止的航行体在某方向突然获得一给定加速度a，可表示为

(5)

a引起的速度分量变化在短时间内相对v为小量，时刻t0前后流体动力的变化量等于航行体加速运动引起的惯性力，因此可直接根据该差值计算附加质量。

附加质量分量

(6)

1.2.2 旋转导数

为获得旋转导数，可模拟物体某方向转动分量突变的流场，有

(7)

式中：Ω为角速度。过程中保持质心沿轴向的线速度v不变，法向及侧向速度为零，如图1所示。

Ω引起的诱导速度相对v为小量，时刻t0前后流体动力的变化量等于航行体旋转诱导的流体动力，因此可直接根据该差值计算旋转导数。

旋转导数近似表示为

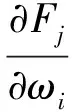
2 数值计算

2.1数值方法验证

分别采用两种方法计算了圆球和椭球附加质量，通过与理论解的比较，对两种数值方法进行验证。

对圆球(半径R=0.4 m)，在无界水中附加质量的理论解为133.8 kg，用基于摇荡运动的附加质量计算方法(方法1)算得的结果为134.5 kg；用基于运动状态突变流场模拟方法(方法2)算得的结果为132.7 kg，两个计算解与势流理论解的误差均小于1%，表明两种方法均可用于计算流体动力参数，并均能获得较高的精度。

对椭球(长轴0.8 m，短轴0.4 m)的附加质量矩阵中，有λ11，λ22，λ33三个独立的非零分量。两种方法得到对应的各附加质量分量见表1。由表1可知：计算结果与势流理论结果也非常一致。

表1 椭球计算得到附加质量

2.2水下航行体的旋转导数

对细长体的附加质量已有较充分的认识，但对其旋转导数还缺乏细致的研究。

本文以一长细比L/D为15的细长柱体为例(如图2所示)，其质心位于航行体形心(几何中心)，头部及底部皆为圆平面，与中段采取光滑过渡。为对各部分受力进行分析，将航行体表面分为14部分，包括头部、底部2个平面，中段平分的柱面10个及连接面2个。

设航行体的航行速度v=10 m/s，在1.0 s之前航行速度方向与航行体轴向一致；从1.0 s开始，航行体绕远处一固定点旋转(定常拉升)(如图1所示)，质心线速度保持10 m/s不变，俯仰角速度ωz=v/R′(此处：R′为航行体质心距离旋转中心的距离)；当ωz=0.1 s-1时，R′=100 m。在短时范围内(如0.988～1.002 s之间)，航行体俯仰角变化较小，可直接用竖直方向的受力代替升力。

数值计算所得叠加转动前后航行体及各部分升力、俯仰力矩系数分别如图3、4所示。不同下标代表图2中航行体表面的不同部分。升力、俯仰力矩系数分别基于垂直于来流方向的流体作用力及绕质心的俯仰力矩的无量纲化获得。由图3、4可知：在t=1.0 s时升力存在一个明显的脉动式振荡，但之后快速趋于稳定。

从各部分对旋转导数的贡献来看，头、尾附近的两个连接面对升力、力矩变化的贡献最大；两连接面及附近两单元面对应的升力旋转导数为负值；中间其他各面对应的升力旋转导数为正值。对细长圆柱体，改变头尾部形状可引起旋转导数的较大改变。

3 结束语

本文参照物理实验构建了通过模拟物体摇荡运动的确定附加质量的方法。通过规则物体附加质量的计算，证明该方法有较好的计算精度。算例结果也间接表明对变速物体绕流流场的数值模拟是有效的，所得的流体动力准确。根据物体变速运动流体动力的变化规律，本文进一步提出了更易于操作的基于运动状态突变流场模拟的附加质量和旋转导数计算方法。通过算例，不但得到了细长航行体包括附加质量和旋转导数的多种流体动力参数，而且获得了流体动力参数的空间分布特征。后续可用本文方法对不同航形体的流体动力特性进行更细致的研究。

[1] 黄祥鹿, 俞湘三, 张东. 振荡圆柱流体动力系数测量[J]. 海洋工程, 1991, 9(4): 29-38.

[2] 王基盛, 杨庆山. 流体环境中结构附加质量的计算[J]. 北方交通大学学报, 2003, 27(1): 40-43.

[3] 刘丹, 王晓亮, 单雪雄. 平流层飞艇的附加质量及其对飞艇运动的影响[J]. 计算机仿真, 2006, 23(6): 52-56.

[4] 勾莹, 滕斌, 宁德志. 波浪与两相连浮体的相互作用[J]. 中国工程科学, 2004, 6(7): 75-80.

[5] 林超友, 朱军. 潜艇近海底航行附加质量数值计算[J]. 船舶工程, 2003, 25(1): 26-29..

[6] 苏海东, 黄玉盈. 求半无限域流场中物体附连水质量的一种简便解法[J]. 土木工程与管理学报, 2003, 20(4): 14-16..

[7] 陈玮琪, 颜开, 史淦君, 等. 基于TSK智能技术的物体垂直出水水动力参数辨识研究[J]. 动力学研究与进展, 2005, 20(4): 446-451.

[8] 庞永杰, 李斌. 支撑方式和模型尺度对轴对称体旋转导数的影响[J]. 哈尔滨工程大学学报, 2005, 26(3): 288-291.

[9] 杨波, 万林, 王骁, 等. 纯横荡和旋臂试验的数值模拟[J]. 舰船科学技术, 2008, 30(4): 138-141.

[10] 肖昌润, 刘瑞杰, 许可, 等. 潜艇旋臂回转试验数值模拟[J]. 江苏科技大学学报, 2014, 28(4): 313-316.

[11] 詹成胜, 刘祖源, 程细得. 潜艇水动力系数数值计算[J]. 船海工程, 2008, 37(4): 1-4.

StudyonHydrodynamicParametersofVehicleBasedonNumericalExperiments

LI Jie1， LI Xiao-lin2， FU Hui-ping1

(1. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China; 2. Shanghai Electromechanical Engineering Institute, Shanghai 201109, China)

The hydrodynamic parameters of vehicle based on numerical experiments were studied in this paper, which were added mass, position derivative and rotational derivative used in trajectory prediction of vehicle. According to Flourier analysis, the inertial force was separated from hydrodynamic force and the method to calculate the added mass was presented. The numerical simulation of flow was finished by using CFD software. On the basis of the above research, another computational method of added mass and pitching dynamic derivative was developed by the numerical simulation of flow around an object undergoing a sudden change of motion state. The calculation samples of sphere and ellipsoid were carried on by the two methods proposed. It showed that the results obtained by the two methods were agreed with the result of potential flow theory. The rotational derivative of underwater vehicle with slender body was computed. The results showed that the two joint planes at the head and tail had the most contribution to the change of lift force and moment and the lift derivatives of the two joint planes and their nearby units were negative but the lift rotation derivatives of other mediate planes were positive. It is possible to obtain not only various hydrodynamic parameters of underwater vehicle with slender body such as added mass and rotational derivative but also the spatial distribution of the hydrodynamic parameters. It is easier to operate and analyze the distribution character of hydrodynamic parameters by numerical simulation of flow around a body with sudden change of motion state.

vehicle; hydrodynamic force; added mass; rotational derivative; numerical experiments; vibrative motion; sudden change of motion state; sphere

1006-1630(2017)05-0105-05

2016-11-28；

2017-03-08

国家自然科学基金资助(11572194)；航天先进技术联合研究中心基金资助(USCAST2015-31)

李 杰(1977—)，男，博士，副研究员，主要研究方向为物体入水、空泡流、水弹道等。

O352

A

10.19328/j.cnki.1006-1630.2017.05.017