自由漂浮柔性航天器的非线性扰动观测器设计
2017-11-04孙凯鹏赵艳彬许域菲毕振瀚
孙凯鹏,廖 鹤,赵艳彬,陈 提,许域菲,毕振瀚
(1.上海卫星工程研究所,上海 201109;2.南京航空航天大学 机械结构力学及控制国家重点实验室,江苏 南京 210016)
自由漂浮柔性航天器的非线性扰动观测器设计
孙凯鹏1,廖 鹤1,赵艳彬1,陈 提2,许域菲1,毕振瀚1
(1.上海卫星工程研究所,上海 201109;2.南京航空航天大学 机械结构力学及控制国家重点实验室,江苏 南京 210016)
为提高控制策略的效率,考虑航天器的平动和转动与柔性附件的振动相互耦合作用,对一种用于估计柔性附件对自由漂浮航天器主体平动和姿态转动影响的非线性扰动观测器(NDO)设计进行了研究。将自由漂浮航天器简化为自由运动的中心刚体柔性梁(FHB)系统,用浮动坐标系建立了系统的动力学模型,并用假设模态法对柔性附件进行离散以方便计算。将与不可观测状态相关的项作为等效扰动项,并假设其为慢变且有界,设计了扰动观测器。因考虑了柔性附件对航天位姿的扰动,设计的扰动观测器具渐近收敛性和鲁棒性。构建了Lyapunov函数,从理论上证明了该观测器的收敛性。用无外力输入的自由运动和受迫运动两个数值仿真算例验证扰动观测器的有效性,结果表明设计的扰动观测器估值与真实值基本一致。研究为后续包含扰动补偿的控制器设计奠定了基础。
自由漂浮; 柔性航天器; 扰动观测器; Lyapunov稳定性; 中心刚体; 柔性梁; 扰动估计; 渐近收敛
0 引言
现代航天工业对柔性航天器控制精度和鲁棒性的要求越来越高,柔性航天器中柔性附件的振动与航天器的平动、姿态运动相互耦合[1-3]。柔性附件的存在会影响航天器定位及姿态指向精度。一种有效的方法是将柔性附件的影响作为对主体的扰动处理,并设计合理的扰动观测器,用于在控制器设计中补偿该部分扰动[4-5]。对非线性扰动观测器进行了大量研究[6-10]。文献[11]对可能存在的噪声、未建模部分设计了扰动观测器,并给出了行星着陆过程的控制器设计。文献[12]设计了一种非线性扰动观测器,并理论证明了该观测器具半全局稳定特性。文献[13]解决了针对非线性系统的未知外部扰动自适应补偿问题,并针对不同情况理论证明了相应的收敛特性。在柔性航天器动力学与控制领域,扰动观测器也得到了广泛关注,如文献[7]基于非线性扰动观测器理念研究了带柔性附件航天器的姿态控制问题;文献[14]针对柔性航天器姿态机动设计了一种基于扰动观测器的反馈线性化控制律。文献[15]研究了柔性机械臂的扰动观测与边界控制问题。但上述研究只考虑了柔性航天器姿态运动中的扰动观测器设计。实际上,在柔性航天器工作过程中,航天器的平动与附件的振荡也相互耦合,在部分高精度航天任务中,必须考虑附件对航天器平动的影响。针对自由漂浮的柔性航天器,本文对一种考虑对航天器平动和姿态转动影响的非线性扰动观测器设计进行了研究,用浮动坐标系方法建立了自由漂浮柔性航天器的动力学方程,将与不可观测状态有关的项作为等效扰动项处理,设计扰动观测器,并用Lyapunov方法理论证明其收敛性,由两个数值仿真算例验证了设计的扰动观测器的有效性。
1 数学模型
自由漂浮柔性航天器模型在航天工业中得到广泛应用,如图1所示。该模型可合理地简化为自由运动的中心刚体柔性梁(FHB)系统。设FHB系统运动速度慢且附件变形小,可用浮动坐标系方法对该系统进行建模。浮动坐标系的核心是将附件的小变形直接叠加到刚体运动上。为便于研究,用假设模态法对柔性附件进行离散。
忽略梁的轴向变形,建立惯性系O-XY和随动坐标系o-xy。设中心刚体的位置矢量ro=[xoyo]T;中心刚体的姿态角为θ;梁上任一点的位置矢量为rA。此处:xo,yo分别为中心刚体质心在惯性系中的X、Y轴坐标。则FHB系统的动能和势能可分别表示为
(1)
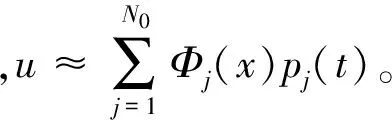
设仅梁的位置姿态可测、可控。则根据Lagrange方程可得系统的动力学方程为
(2)
式中:M,C分别为质量矩阵和阻尼矩阵;g(q)为刚度项,且g(q)=∂V/∂q=Kq;τ为广义外力矢量,且
τi=[FxFyT00]T=[(τi1)T0]T

2 扰动观测器设计
为便于设计观测器,将式(2)改写为以下形式
(3)
式中:M1,C1分别为刚体运动质量矩阵和阻尼矩阵;M4,C4,K4分别为弹性变形质量项、阻尼项和刚度项;M2,M3分别为刚体运动与弹性变形的耦合质量矩阵;C2,C3分别为刚体运动与弹性变形的耦合阻尼矩阵;X为由刚体位置和姿态决定的矢量。
分析式(3)中的第一部分方程
(4)
(5)

(6)
航天器附件尺度一般很大,频率很低,因此假设等效扰动项d为慢变且有界。为估计系统式(6)中的d,构建扰动观测器
(7)
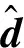
(8)
定义de为扰动观测误差,则
(9)
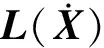
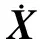
(10)
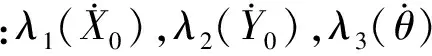
证明:选择Lyapunov函数
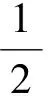
(11)
计算其导数
(12)
3 数值算例
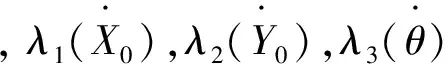
算例1:设无外力输入状况下,给定初始旋转角速度0.1 rad/s和梁末端初始变形0.1 m,使系统自由运动,计算所得扰动矢量的第一、第二、第三项分别如图2~4所示。由图2~4可知:扰动矢量三个方向的分量估值与真实值较吻合,误差很小。
算例2:设三个控制输入均为幅值0.01、圆频率0.1的正弦信号,即Fx,Fy,T0均为0.01sin(0.1t),计算所得扰动矢量的第一、第二、第三项分别如图5~7所示。由图5~7可知:估值与真实值几乎一致。
4 结束语
本文主要的研究对象是自由漂浮的带柔性附件航天器。将柔性附件产生的动力学影响描述成对主体航天器的扰动处理,并针对该种扰动设计了一种非线性观测器,并从理论上证明了观测器的收敛性,两个数值仿真计算结果表明:设计的扰动观测器估值与真实值基本一致,为后续包含扰动补偿的控制器设计奠定了基础。与前人研究相比,本文考虑了柔性附件对航天位姿的扰动,设计的扰动观测器具渐近收敛性,由此也有一定的鲁棒性。后续研究可考虑将该扰动观测器作为扰动补偿用于控制器设计,补偿航天器柔性附件对本体定位及姿态指向精度的影响。
[1] 黄文虎, 曹登庆, 韩增尧. 航天器动力学与控制的研究进展与展望[J]. 力学进展, 2012, 42(4): 367-394.
[2] 蒋建平, 李东旭. 带太阳帆板航天器刚柔耦合动力学研究[J]. 航空学报, 2006, 27(3): 418-422.
[3] CHEN T, WEN H, HU H, et al. Output consensus and collision avoidance of a team of flexible spacecraft for on-orbit autonomous assembly[J]. Acta Astronautica, 2016, 121: 271-281.
[4] GUO L, CAO S. Anti-disturbance control theory for systems with multiple disturbances: a survey[J]. ISA Transactions, 2014, 53(4): 846-849.
[5] YANG H, LIU J. Distributed piezoelectric vibration control for a flexible-link manipulator based on an observer in the form of partial differential equations[J]. Journal of Sound and Vibration, 2016, 363: 77-96.
[6] ZHANG R, LI T, GUO L. Disturbance observer based control for flexible spacecraft with time-varying input delay[J]. Advances in Difference Equations, 2013, 2013(1): 1-12.
[7] LIU H, GUO L, ZHANG Y. An anti-disturbance PD control scheme for attitude control and stabilization of flexible spacecrafts[J]. Nonlinear Dynamics, 2012, 67(3): 2081-2088.
[8] CHEN W H. Disturbance observer based control for nonlinear systems[J]. IEEE/ASME Transactions on Mechatronics, 2004, 9(4): 706-710.
[9] CHEN W, YANG J, GUO L, et al. Disturbance-observer-based control and related methods: an overview[J]. IEEE Transactions on Industrial Electronics, 2016, 63(2): 1083-1095.
[10] 吴忠, 黄丽雅, 魏孔明, 等. 航天器姿态自抗扰控制[J]. 控制理论与应用, 2013, 30(12): 1617-1622.
[11] CANUTO E, MOLANO-JIMENEZ A, PEREZ-MONTENEGRO C. Disturbance rejection in space applications: problems and solutions[J]. Acta Astronautica, 2012, 72: 121-131.
[12] BACK J, SHIM H. Adding robustness to nominal output-feedback controllers for uncertain nonlinear systems: a nonlinear version of disturbance observer[J]. Automatica, 2008, 44(10): 2528-2537.
[13] NIKIFOROV V O. Nonlinear servocompensation of unknown external disturbances[J]. Automatica, 2001, 37(10): 1647-1653.
[14] WANG Z, WU Z. Nonlinear attitude control scheme with disturbance observer for flexible spacecrafts[J]. Nonlinear Dynamics, 2015, 81(1-2): 257-264.
[15] JIANG T, LIU J, HE W. Boundary control for a flexible manipulator based on infinite dimensional disturbance observer[J]. Journal of Sound and Vibration, 2015, 348: 1-14.
NonlinearDisturbanceObserverDesignforFree-FloatingFlexibleSpacecrafts
SUN Kai-peng1, LIAO He1, ZHAO Yan-bin1, CHEN Ti2, XU Yu-fei1, BI Zhen-han1
(1. Shanghai Institute of Satellite Engineering, Shanghai 201109, China; 2. State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, Jiangsu, China)
To improve the control efficiency, the design of nonlinear disturbance observer (NDO) was studied to estimate the influence of the flexible appendage on the translational and rotational motions of the spacecraft’s main body for free-floating flexible spacecrafts with the coupling between the translational and rotational motion of the spacecraft and the vibration of the flexible appendage in this paper. The floating spacecraft was simplified as free hub beam (FHB). The dynamic equations of the system were established by floating coordinate system. The flexible appendage was discrete for computation convenience by assumed mode method. The all terms related with non-observed state were treated as the equivalent disturbance, and it was assumed that they were slow changed and bound constrained. The observer was designed, which had asymptotic convergence and robustness because the disturbance of the flexible appendage on the position and attitude of the spacecraft was in consideration. The Lyapunov function was given to prove the convergence of the observer designed theoretically. Two numerical simulations which were free motion without force input and forced motion were computed to verify the effectiveness of the observer designed. The results showed that the estimation by the observer designed was well agreed with the true value. The study is valuable for latter controller design including disturbance compensation.
free-floating; flexible spacecraft; disturbance observer; Lyapunov stability; hub; beam; disturbance estimation; asymptotic convergence
1006-1630(2017)05-0054-05
2016-11-10;
2017-02-20
国家自然科学基金资助(11602145);国家重点研发计划专项资助(2016YFB0500801);上海市科学技术委员会启明星计划(B类)资助(16QB1403500)
孙凯鹏(1987—),男,博士,主要从事卫星总体与结构技术研究。
V448.2
A
10.19328/j.cnki.1006-1630.2017.05.008
