一种基于推力器控制的卫星质心在轨估算方法研究
2017-11-04郭正勇张增安汪礼成何益康赵永德
郭正勇,张增安,汪礼成,何益康,赵永德
(上海航天控制技术研究所,上海 201109)
一种基于推力器控制的卫星质心在轨估算方法研究
郭正勇,张增安,汪礼成,何益康,赵永德
(上海航天控制技术研究所,上海 201109)
为准确估计地球静止轨道(GEO)卫星在轨道机动过程中因燃料消耗产生的质心位置的变化,提出了一种基于推力器连续喷气的卫星质心在轨估算方法。采用推力器在固定时间内连续喷气工作方式以形成恒定的推力器作用力和力矩,根据陀螺测量值用最小二乘法估算推力器产生的星体角加速度值,采用产生正负向相反控制力矩的两个推力器同时工作,以减小对卫星姿态的扰动和三轴间的动力学耦合。给出了卫星质心计算公式,讨论了质心估算中的推力器推力位置测量误差、推力器推力矢量方向角度测量误差、成对工作推力器推力大小偏差、陀螺组合测量噪声、整星转动惯量计算偏差,以及卫星姿态动力学耦合特性等主要误差源对估算结果的影响。基于某GEO卫星的推力器数据,计算获得了在轨质心的总测量偏差。仿真结果表明:理论计算值与仿真结果的误差在允许范围内,方法有效,可广泛用于航天器的质心位置测量,方法有较大的工程应用价值。
地球静止卫星; 卫星质心估算; 推力器; 陀螺; 连续喷气; 最小二乘法; 误差源; 测量偏差
0 引言
某地球静止轨道卫星采用双组元液体推进系统,4个燃料储箱采用并联布局方式,在轨道机动过程中约80%的燃料被消耗。由于储箱排放不均衡及混合比偏差的影响,卫星的质心位置变化较大,且地面难以实现整个变轨期间的质量特性计算,有可能导致490 N变轨发动机因推力偏心产生的干扰力矩变大,增大姿控推力器消耗的燃料。因此,有必要对卫星的质心位置进行在轨估算,为储箱的均衡排放控制和混合比调节提供参考[1]。目前,国内外对卫星在轨质量特性计算方法进行了研究,但多数采用对敏感器数据进行连续处理,数据量大、计算复杂,且未考虑敏感器测量误差、推力器推力误差等的影响[2-3]。文献[4-6]用递推最小二乘法对质心位置进行估算,以推力器作为执行机构,缺点是卫星在轨运行过程中,由于推力器喷气为随机的,导致辨识过程时间长;文献[7]提出了基于角动量装置的质心位置估算方法,不消耗星上燃料,但要求配置高精度的加速度测量装置,增加了系统配置;文献[8]提出了仅根据星敏感器测量信息,用卡尔曼滤波算法对卫星的三轴转动惯量进行估计,但不能实现对卫星质心位置的辨识;文献[9]将飞轮、推力器分别作为卫星转动惯量、质心位置辨识的执行结构,用最小二乘法分步实现对卫星质量特性的辨识,但存在与文献[3]相同的问题。
推力器产生的力矩与推力器的推力、卫星的质心位置有关,可采用推力器喷气的方式,根据卫星姿态动力学方程,利用卫星角加速度、角速度信息,结合推力器的安装可估算出卫星的质心位置[10-12]。因某GEO卫星未安装角加速度计,需利用陀螺测量值较精确地估算星体角速度值,要求质心测量过程中卫星的角加速度为常值,即推力器产生的作用力及力矩恒定。为此,在不增加额外测量装置的条件下,本文提出了一种基于推力器固定时间内连续喷气的方法以实现对卫星质心位置估算,用最小二乘法对陀螺测量数据进行处理,估计卫星角加速度,进而计算卫星的质心位置,讨论了不同误差源的影响,分析了质心估算精度。
1 问题描述
1.1坐标系定义
卫星机械坐标系:为正交坐标系且与星体固定,是卫星安装布局坐标系,星上单机的安装布局及质心位置均在该坐标系中描述。坐标原点Oj为平台承力筒分离面的几何中心;OjZj轴垂直于星箭分离面,指向卫星本体的对地面板,此轴亦为卫星的纵轴;OjYj轴垂直于指向卫星本体的南面板,与太阳电池阵驱动轴线平行;OjXj轴由右手法则确定。
卫星本体坐标系:与卫星本体固连,由机械坐标系的坐标原点平移至卫星质心后形成。坐标原点Ob为卫星质心;ObXb、ObYb、ObZb轴为卫星的三个几何轴,与机械坐标系的相应轴平行,分别称为滚动轴、俯仰轴和偏航轴。
1.2推力器安装布局
卫星姿控推力器的安装布局如图1所示。在标称条件下,推力器在卫星本体坐标系中产生的力和力矩见表1。
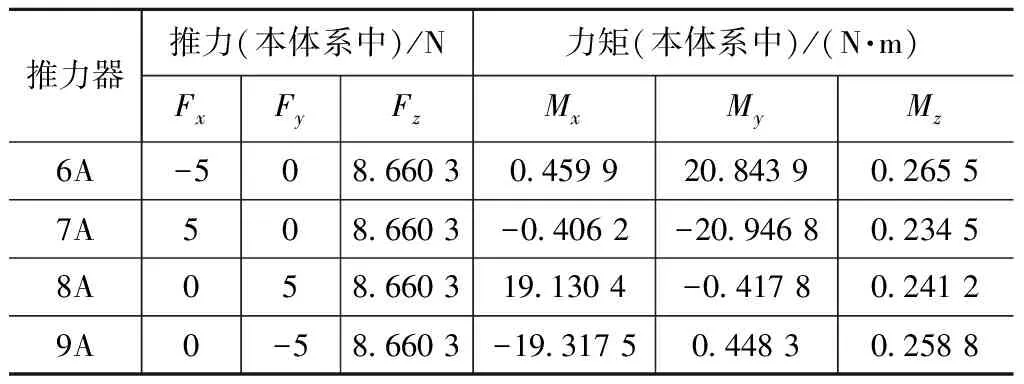
推力器推力(本体系中)/N力矩(本体系中)/(N·m)FxFyFzMxMyMz6A-508660304599208439026557A5086603-04062-209468023458A0586603191304-04178024129A0-586603-1931750448302588
由表1可知:推力器6A/7A、8A/9A主要在俯仰、滚动向产生较大的控制力矩,同时会在其他方向产生附加力矩。
2 卫星质心位置估算
2.1推力器工作方式选择
由于电磁阀动作时延的影响,推力器存在推力延时特性。在接收到喷气脉冲时间指令时,推力器实际输出的动态特性如图2所示。
由图1,因推力器自身存在的前、后时延等影响,推力器实际输出的推力与标称推力存在偏差,特别是当指令喷气时间Tn较小时,推力器实际输出的推力大小与标称值存在偏差较大,且产生推力的大小变化较大。
为保证质心测量过程中推力器产生的推力近似为恒值,在质心测量过程中采用推力器在固定时间内连续喷气的工作方式。另外,为防止卫星三轴角速度过大,减小对卫星姿态的扰动及三轴间的动力学耦合作用,选择产生正、负方向相反控制力矩的两个推力器同时工作。
2.2陀螺测量数据处理

2.3质心位置计算
卫星在轨运行过程中,环境干扰力矩(重力梯度力矩、地磁力矩、太阳光压力矩等)远小于推力器产生的力矩,可认为三轴惯性角速度变化由推力器引起。质心位置测量过程中,选择产生正、负相反的控制力矩的两个推力器同时喷气(表1中推力器6A与7A、8A与9A),对卫星产生的扰动力矩较小,因此在测量过程中卫星角速度较小,姿态动力学方程可简化为
(1)
式中:Ixx,Iyy,Izz分别为卫星滚动、俯仰和偏航向主惯量;ωx,ωy,ωz分别为卫星三轴惯性角速度;Tx,Ty,Tz分别为卫星三个方向受到的外部力矩。
推力器6A、7A同时工作,喷气时间长度为Δt1,陀螺组合测得卫星三轴惯性角速度增量分别为Δωx67,Δωy67,Δωz67,由姿态动力学方程及力矩计算公式可得



(2)
式中:py为卫星y向质心位置;F6a,F7a分别为推力器6A、7A产生的推力幅值;p6ay,α6,γ6分别为推力器6A在机械坐标系中的y向位置坐标、推力的滚动向余弦角和偏航向余弦角;p7ay,α7,γ7分别为推力器7A在机械坐标系中的y向位置坐标、推力滚动向余弦角和推力偏航向余弦角,均可在安装时测量可得。
根据假设条件,质心测量过程中推力器产生的推力大小为恒定值,对式(2)分子、分母同时求导,则式(2)可变为




(3)
通过推力标定和选择,成对工作的推力器产生的推力大小偏差≤2%,有F6a/F7a≈1,则式(3)可变为

(4)



(5)

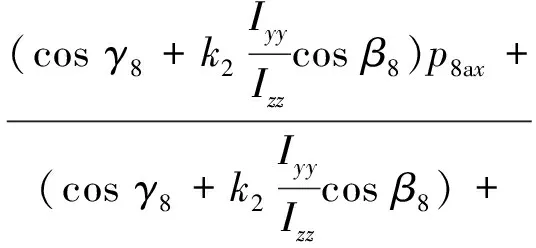

(6)
式中:p8ax,β8,γ8分别为推力器8A在机械坐标系中的x向位置坐标、推力俯仰向余弦角和偏航向余弦角;p9ax,β9,γ9分别为推力器9A在机械坐标系中的x向位置坐标、推力俯仰向余弦角和偏航向余弦角,均可在安装时测得。
3 测量误差分析
由式(5)、(6)可知:质心测量的误差源主要有推力器产生的推力位置测量误差、推力器产生的推力矢量的方向角度测量误差、成对工作的推力器的推力大小偏差、陀螺组合测量噪声、整星转动惯量计算偏差,以及卫星姿态动力学耦合特性等引起质心测量的偏差。
除整星转动惯量计算偏差外,其他误差源主要引起k1,k2值的变化。设由遥测数据算得的k1,k2的值相对标称值的偏差分别为Δk1,Δk2,卫星质心位置的估算误差Δp=[ΔpxΔpy],则在小偏差条件下有
(7)
3.1陀螺测量噪声导致的误差
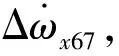

同理可得

可知当推力器工作时间长度越长,陀螺测量噪声的影响相对较小。以推力器工作时间10 s,陀螺组合随机测量噪声δω=0.06 (°)/h(3σ),可算得陀螺组合测量噪声引起的x、y向质心测量误差分别为Δpx=0.002 mm,Δpy=0.003 mm。
3.2推力器推力方向偏差导致的误差
因推力器本身的性能导致推力器的推力分量与标称值存在偏差,由k1,k2的表达式可得推力器推力矢量角度偏差引起的k1,k2偏差分别近似为

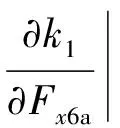
(8)


(9)
由式(8)、(9)可得推力器的推力变化对k1,k2的影响,由此可确定k1,k2值影响的最坏工况条件。
考虑推力器的推力方向角度偏差0.1°,最坏工况条件下可得推力器推力方向偏差引起的质心估算误差为Δpx=0.045 mm,Δpy=0.041 mm。
3.3推力器推力位置偏差导致的误差
因推力器产生的推力实际位置与喷管法兰中心存在偏差,由k1,k2的表达式可得推力器推力矢量角度偏差引起的k1,k2的偏差分别近似为
(10)
分析可得:推力器6A、7A的y向位置坐标存在同向偏差时引起k1的误差最大;推力器8A、9A的x向位置坐标存在同向偏差时引起k2的误差最大。则推力器的推力位置偏差为1.5 mm时,引起的卫星x、y向质心位置坐标的最大估算误差为1.5 mm。
3.4成对工作推力器推力大小偏差导致的误差
考虑成对工作的两个推力器产生的推力大小偏差对质心估算精度的影响。令推力器6A、7A产生的推力大小之比kF67=F6a/F7a,推力器8A、9A产生的推力大小之比kF89=F8a/F9a,则由式(3)可得


(11)


(12)
同时工作的两推力器产生的推力大小存在偏差,在小偏差条件下近似有
(13)
考虑成对工作的推力器产生的推力大小偏差小于2%,最坏工况条件下由式(7)、(13)可算得Δpx=0.5 mm,Δpy=0.498 mm。
3.5卫星转动惯量计算偏差导致的误差
实际工程中,卫星在轨的转动惯量理论计算值与实际值存在误差。考虑卫星的实际转动惯量与理论值间的误差为10%,考虑最坏工况组合条件

0.18k1non
(14)
0.18k2non
(15)
式中:下标non表示标称值。
代入式(5),可得最坏工况条件下卫星质量特性计算偏差引起卫星x向质心最大测量误差约0.352 mm,y向约0.62 mm。通过在轨对卫星转动惯量进行估算后,由转动惯量计算偏差导致的质心测量误差可忽略。
3.6三轴耦合运动导致的误差
由于惯量积、陀螺力矩的存在,导致三轴间的耦合会对质心测量精度产生一定的影响。三轴间耦合运动引起的k1,k2的变化可分别表示为
将上述计算值代入式(5),可算得三轴耦合运动引起的x、y向质心测量误差分别为Δpx=0.01 mm,Δpy=0.434 mm。
3.7太阳帆板振动的影响
在质心测量过程中,推力器工作会引起太阳帆板挠性振动,导致卫星三轴惯性角速度存在周期性变化,其变化为高频分量。数据处理过程中通过数据拟合的方式可基本消除帆板振动的影响,因此可忽略帆板振动对质心测量的影响。
3.8总测量误差
影响测量误差的不同因素综合结果见表2。由表2可知:三轴耦合运动导致卫星y向质心位置的测量误差相对较大,最大测量偏差约3.1 mm。
4 仿真验证
通过控制推力器6A与7A、8A与9A同时喷气,将喷气期间的陀螺测得卫星三轴惯性角速度数据遥测下传,通过对陀螺测量数据进行处理,可得推力器产生的卫星惯性角加速度,卫星三轴惯性角速度变化如图3所示。代入式(3)、(4)后可算得卫星质心位置,质心估算结果见表3。
由仿真结果可知:
a)不考虑拉偏时,卫星的质心测量精度优于0.5 mm;考虑成对工作的推力器产生的推力偏差,质心测量误差约0.4 mm;考虑卫星转动惯量误差,质心测量误差约1.5 mm。
b)数学仿真结果与理论分析结果的误差在可允许范围内,数学仿真结果表明理论分析的准确性。
5 结束语
本文提出了一种基于推力器、陀螺组合的卫星质心位置估计的方法。该方法不需配置角加速度测量装置,通过将陀螺测量数据进行遥测下传,经由地面数据处理估算出卫星的质心位置。该方法简化了数据处理过程,避免了以往利用卡尔曼滤波估计等算法时计算量大的缺点;通过采用一对产生方向相反力矩的推力器在固定时间内连续同时工作的方式,避免了推力器的推力大小变化引起的角加速度变化偏差,提高了质心测量精度。该方法可广泛用于航天器的质心位置测量,为航天器储箱混合比偏差、不均衡排放的调整提供依据,具有较大的工程应用价值。
该方法在计算过程中用到了卫星的转动惯量,由于卫星实际的转动惯量与计算值存在偏差,从而带来卫星质心位置的测量误差。在下一步研究中,应考虑对卫星转动惯量进行在轨估算,减少转动惯量计算值与实际值之间的偏差,以提高质心测量的精度。

表3 质心测量数学仿真结果
[1] 屠善澄. 卫星姿态动力学与控制(2)[M]. 北京: 中国宇航出版社, 2009.
[2] 李春华. 航天器动态质量特性分析[J]. 航天器工程, 2005, 14(3): 15-20.
[3] 张洪波, 武向军, 刘天雄, 等. 一种在轨卫星质量特性计算方法[J]. 航天器工程, 2013, 22(6): 30-36.
[4] 王书廷, 曹喜滨. 卫星质量特性的在线辨识算法研究[C]∥第25届中国控制会议. 哈尔滨: [s. n.], 2006: 524-528.
[5] WILSON E, SUTTER D W. Motion-based mass and thruster-property identification for thruster-controlled spacecraft[R]. AIAA, 2005-6907, 2005.
[6] WILSON E, LAGES C, MAH R. On-line, gyro-based, mass-property identification for thruster-controlled spacecraft using recursive least squares[C]∥The 45th Midwest Symposium on Circuits and Systems. Tuls: [s. n.], 2002: 334-337.
[7] BERGMANN E. Spacecraft mass property identification with torque-generating control[J]. Journal of Guidance Control and Dynamics, 1990, 13(1): 99-103.
[8] SU J J, BBAN H. Mass Property estimation of gyroless spacecraft[C]∥ 11thInternational Conference on Control, Automation and Systems. KINTEX, Gyeonggi-do: [s. n.], 2011: 1884-1887.
[9] 徐文福, 何勇, 王学谦, 等. 航天器质量特性参数的在轨辨识方法[J]. 宇航学报, 2010, 31(8): 1905-1914.
[10] 刘伟霞, 熊智, 郁丰, 等. 组合航天器转动惯量在轨两步辨识标定[J]. 中国空间科学技术, 2013, 33(2): 32-39.
[11] BERGMANN E V, WALKER B K, LEVY D R. Mass property estimation for control of asymmetrical satellites[J]. Journal of Guidance, Control, and Dynamics, 1987, 10: 483-491.
[12] TANYGIN S, WILLIAMS T. Mass property estimation using coasting maneuvers[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(4): 625-632.
StudyofOn-OrbitEstimationMethodofSatellite’CentroidBasedonThrustControl
GUO Zheng-yong, ZHANG Zeng-an, WANG Li-cheng, HE Yi-kang, ZHAO Yong-de
(Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China)
To identify the centroid change of on-orbit geostationary satellite caused by propellant consumption, an on-orbit centroid estimation method with thruster’s continuous jet was put forward in this paper. Constant thrust and torque of the thruster were performed through continuous jet during fixed time period. Angular acceleration of satellite produced by thruster was estimated by the least squares-based algorithms according to the gyro measurements. The two thrusters which produced control torques with opposite directions were operating at the same time, which would reduce disturbance of satellite attitude and dynamic coupling among three axes. The computation equations for centroid were given. The effects of main factors on centroid estimation error were discussed, which were thrust position measurement error of thruster, angular measurement error of thrust vector of thruster, thrust value difference between the two thrusters operated, measurement noise of gyros unit, calculation error of rotational inertia of the whole satellite, and dynamic coupled characteristics of satellite attitude. Based on the trust of some GEO satellite, the total on-orbit estimation error of centroid was obtained. The simulation results showed that the difference between the computation and simulation was allowed. The method proposed is effective and has its value in engineering application, which can be used in the measurement of spaceraft centrold.
geostationary orbit satellite; satellite centroid estimation; thruster; gyro; continuous jet; the least squares-based algorithms; error source; estimation error
1006-1630(2017)05-0076-07
2016-12-28;
2017-03-14
国家重大航天工程
郭正勇(1986—),男,工程师,主要从事卫星姿态动力学建模及高精度姿态控制等研究。
V412.4
A
10.19328/j.cnki.1006-1630.2017.05.012
