贯通“构造”之路 激活“生成”之径——以“反比例函数复习”的学材再建构为例

■徐 强

贯通“构造”之路 激活“生成”之径
——以“反比例函数复习”的学材再建构为例

■徐 强

笔者曾参加南通市组织的“自学·议论·引导”教学研讨活动，观摩了一节反比例函数复习课，在且听且思中，得到启发，形成了不同的想法。听完课笔者与同伴探讨后，又有了新的思维碰撞，产生了重新设计的欲望，现整理呈现原教学设计流程与二次教学感悟，与同行交流。

一、原设计再现与反思

1.读图。

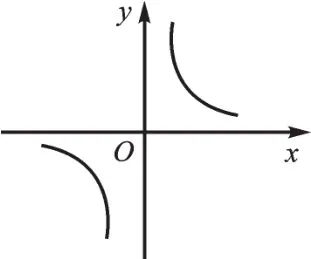
图1

图2

如图1，你能从给出的图像中获得哪些信息？

2.添点。

如图2，（1）图像上有一个点A（2，3），你能得到哪些结论？

（2）你能快速说出一个也在这个函数图像上的点吗？

（3）若m＞0，点D（m，y1），E（m+2，y2），F（-m，y3）三点在这个反比例函数图像上，则y1、y2、y3的大小关系是 。

3.添直线。

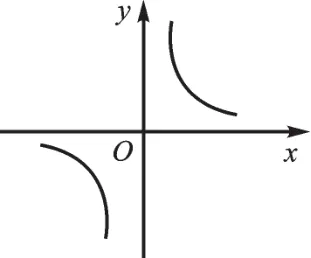
图3

图4

（2）若把第（1）问中k＞0去掉，k的值是多少？

【感受反思】

本节复习课从整体设计而言，四部分问题设置巧妙，以开放题型呈现，力求让每一个学生都有思考的空间“读图”，以开放性问题为载体，引导学生回顾已学的内容，建构知识体系。从实施效果来看，学生基本能梳理出反比例函数的图形、定义、性质，形成了本章内容的知识框架。“添点”，强化已知一点，渗透了基本技能与基本方法，可以利用待定系数法求反比例函数解析式，同时解决了“比较反比例函数值的大小”问题，从实施效果来看，学生的方法让人大开眼界，渗透了数形结合等思想方法。“添线”，进一步挖掘反比例内涵本质，如对称性、“k”的几何意义、求方程组的解、求不等式的解集、图形的面积转化等，逐层深入，不断生成。从实施来看，尤其通过添曲线，学生明白在同一象限的两支与不同象限的两支中形成的三角形面积之间的一种联系，积为3的三角形吗？

（3）画直线OA，与双曲线的另一支相交于点B，点B的坐标是多少？

（4）图像上有另一点C（6，1），画直线BC，观察图形你能得到哪些结论？

（5）过点A、C分别向x轴作垂线，垂足分别为E、F，连接OC、OA、AE与OC相交于点D，图中有面积相等的图形吗？

4.添曲线。从而体现知识的一种融合，但效果一般。

从生本角度来看，笔者感到文本设计重点不突出，学生对“添直线”中的（4）（5）问反应较差，实属问题的起点较高。另外，四个环节没有做好无缝对接与整合，问题演变过程中没有让学生在头脑中有一个整体架构，构造跳跃且生硬，没有很好地生成学一题通一类。基于此笔者将该节课进行以下优化重构并教学。

二、二次设计与意图

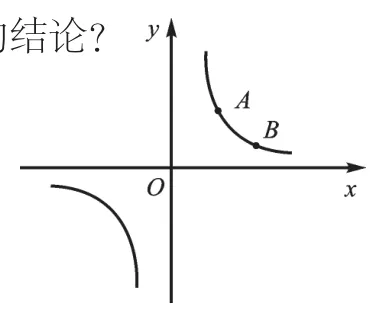
图5

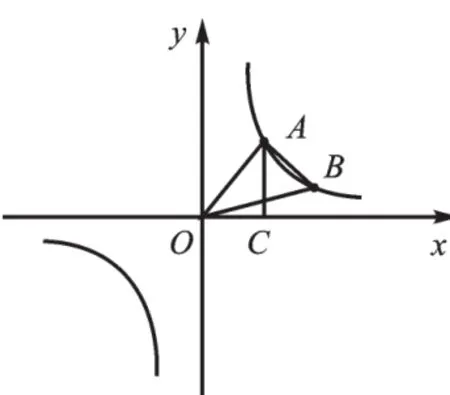
图6

【设计意图】强调反比例函数增减性，也可挖掘比较字母a、b的大小关系的三种不同路径，同时为用待定系数法求函数解析式打下伏笔。

追问1：如果想求字母k的值，原已知条件中，还需增加哪些条件？

【设计意图】强化待定系数法求函数关系式的条件，学生易得出：（1）已知一点，即给出字母a或b的值；（2）已知字母a与b之间存在某一数量关系；（3）已知某一特定图形的面积（如图6，作AC⊥x轴于点C，若S△OAC=3）。教师可进行补充与引导。

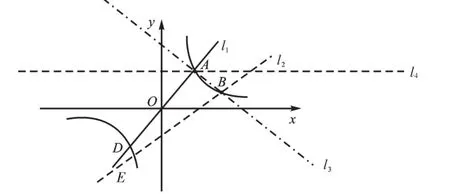
图7

追问3：如图7，如果过点A作一直线l1过原点，交另一支于点D，你能说出点D的坐标吗？

追问4：如图7，如果过点B作直线l2（不过原点），交另一支于点E，你能说出点E的坐标吗？不能的话，还需增加哪些条件？

追问5：如图7，你能比较一次函数l1与反比例函数的值的大小关系吗？

变式：如图7，（1）若过A、B两点作直线l3，一次函数l3与反比例函数的值的大小如何确定呢？

（2）若过A作直线l4‖x轴，当x≤2时，求y的取值范围。

【设计意图】探究如何求“原点三角形面积”（这里的原点三角形指一次函数与反比例函数图像交点及原点形成的三角形），旨在让学生形成基本策略，可以利用反比例函数的对称性或者方程组求交点坐标。

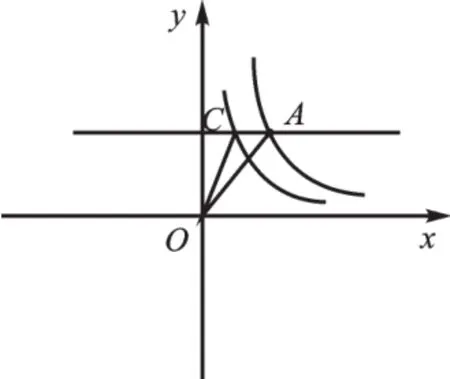
图8

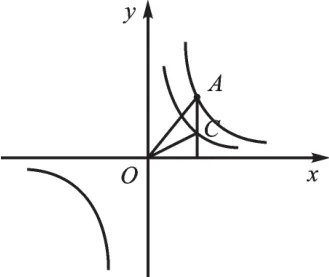
图9

变式1：如图9，平行于y轴的直线分别交两条曲线于A、C两点，求S△AOC= 。

变式3：如图11，在变式2的基础上，若点D是x轴上一动点，求S△ADC= 。

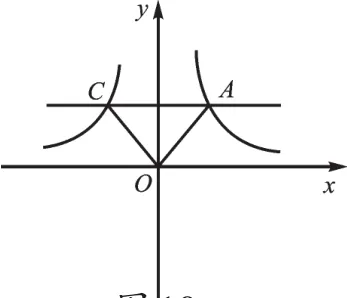
图10

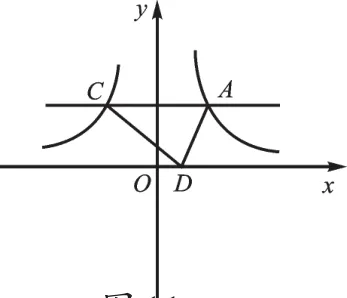
图11

图12

【设计意图】体现三大变化：（1）从双曲线的一支过渡到不同的两支；（2）从同一象限变化到不同象限；（3）平行于坐标轴的直线由一条变化为两条。意在从单纯的一条直线（曲线），进行思维的发散，形成知识的生长点，在辨析中让学生学会方法归纳、学会一题多变等。

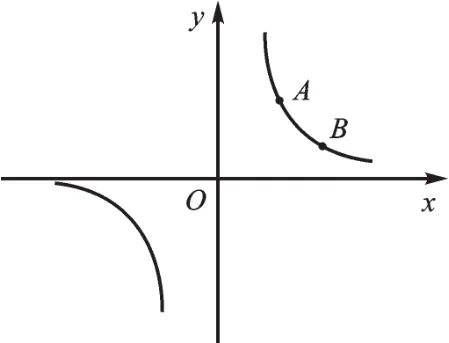
图13

追 问 7：如 图13，已知A（2，6）、B（3，b）是反比例函数的图像上两点。点P是x轴上一动点，是否存在点P，使△ABP为直角三角形？

【设计意图】在复习完反比例函数基础知识的框架下，进一步挖掘数学知识的贯通性，研究基本图形的存在性，旨在教会学生如何借助几何图形的相关性质，在反比例函数背景下有效解决问题，以此培养学生举一反三的能力，真正有的放矢，直击思维要点。

三、教学感悟

1.开放设问，构建知识框架。

本课例，从问题的不断追问中，可以让学生自觉地完成知识的巩固、方法的归纳，一节课后，学生不仅可以形成一张完整的知识框架图，而且可以积累解决问题的方法与策略，收获探究的乐趣、交流的快乐、成功的喜悦。

2.学材整合，寻求贯通融合。

我们知道复习课的关键还在于把学生零散的知识串起来，形成一根主线，加上知识的相互渗透与融合，才能让学生在“攀梯”的过程中，感觉水到渠成，不断收获。如本课中，求反比例函数解析式，不是单纯地给予一个点，而是让学生挖掘求解析式的思路有哪些，同时方程、不等式、几何图形的面积求解等自然蕴含问题之中，让本单元的知识内部有了一种贯通与迁移，构建出属于学生的有效教材。

3.变式训练，聚焦思维提升。

变式的目的是为了让学生在不同背景与不同条件下有自我的认识、解决问题的思路、转化的意识，在知识生长的过程中，思维品质得到进一步提升。如本课设计主线为添点、添线与添图，点由一个过渡到两个，线由直线变化为曲线，同时改变点与线的位置关系，变换图形的形状，不断激发学生探究的欲望，在此过程中让学生找到图形构造之路，解决问题之径。

四、结束语

二次设计实施取得了较好的教学效果，参与听课的老师一致认为，不仅借鉴了原设计的优点，让复习课“老歌”新唱，焕发生命的活力，而且从一个简单问题出发，逐步顺势延伸探究，贯通了“构造”之路，激活了“生成”之径，使问题驱动更具系列性、适切性，问题解决更具规律性、反思性。预设后，注重追问，无论形式还是内容上都能聚焦思想方法，有效突破了重、难点，实施中发挥了学生的最大原动力，主体的作用得以充分体现，把课堂还给了学生。

注：本文是江苏省教育科学“十三五”规划初中重点资助课题《初中数学“学材再建构”研究》（课题编号：E-a/2016/06；主持人：施俊进、徐强）主要研究成果之一。

（作者为江苏省海门市中小学教师研修中心初中数学教研员）