提炼生活模型 规范概念教学——苏科版“数轴”解读、设计与思考

■朱宸材

提炼生活模型 规范概念教学
——苏科版“数轴”解读、设计与思考

■朱宸材

最近，笔者在自己学校的教研组开展了一次组内公开课，课题是苏科版《数学》七年级上册的“数轴”，以下是笔者对教材素材解读、教学过程设计的整理和反思，在此进行分享与交流。

一、教材与教学分析

“数轴”一课是苏科版《数学》七年级上册第二章的核心知识。在引进了负数的概念和有理数分类的前提下，本节课通过引入实际问题而引入展开。作为重要的学习数学和研究数学的工具之一——数轴，主要的作用是对有理数进行直观的描述，比较有理数的大小，引出相反数和绝对值等重要概念，为今后有理数运算法则的推导打下基础，而数轴概念的教学又对于今后的数学概念的教学有着重要的影响和指导作用。同时，数轴是今后构建平面直角坐标系的基础，让学生充分理解对于后续函数部分的学习有着积极的作用。从另外一条主线——数学思想方法的层面来看，数轴建立起了数与形之间的重要联系，数轴可以直观地表示数，又可以进行数字之间的大小比较，在生活中也有着广泛的应用。由此，确定本节课的教学重点：（1）数轴的概念和画法；（2）通过所画的数轴进行有理数大小比较。本课的难点是数轴的建模过程，这需要学生对概念的把握和理解，比较难把握的是建立有理数与数轴上的点的对应关系。

二、教学设计及流程

环节1：创设情境，引入新知。

情境引入：

【情境一】

根据目前的勘测，珠穆朗玛峰高出海平面8844米，而吐鲁番盆地低于海平面155米。如果记海平面为0米，那么珠峰和吐鲁番盆地的高度各是多少？同学们，你会用图形表示吗？

【情境二】

小强从学校出发，向东走50米到达新华书店，如果他向西走，则行走300米可以回到家。在这里，我们明确一下方向：以向东作为正方向，那么小明从学校出发，书店的位置应该如何表示？家的位置又应该怎样表示？请在图中进行正确地表达。

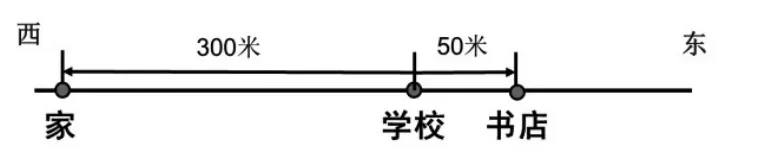
【情境三】

同学们，根据图中的温度计的显示，你能迅速说出上面的读数吗？请仔细观察温度计的构造，想一想，这样的构造具有怎样的特点？

进一步思考：

这3张温度计的图有什么共同特征？我们能否通过一张图来共同表示呢？（能否用一条直线来表示有理数？）

【问题1】什么是数轴？你能用语言来概述一下吗？

让学生通过观察与实践，自己先说出对数轴的大致理解，然后由教师进行补充和说明。

通过温度计作为演示，学生可以形象地理解数轴就像是一个横放的温度计，或者通过刻度尺来进行形象化解释也是可行的。

环节2：理解概念。

【问题2】数轴应该如何来画呢？

①画一条水平直线，在直线上取一点表示0，作为原点。

②规定水平向右的方向为正方向，向左的方向规定为负方向，标出箭头。

③取适当长度为单位长度，在直线上，原点向右每隔一个单位长度取点，依次表示数1、2、3……，从原点向左每隔一个单位长度取点，表示数-1、-2、-3……

像这样规定了原点、正方向、单位长度的直线叫作数轴，通常称原点、正方向和单位长度为数轴的3要素。

【问题2】思考：下面7张图中，哪些是数轴，哪些不是数轴，为什么？

通过辨析加强对数轴概念的理解与认识。

环节3：概念应用，数形结合。

再来看一看通过怎样的方法来表示一个有理数，通过一组问题加强思考：

（1）0与正数、负数相对于数轴分别在什么位置？

（2）如何在数轴上表示整数？

（3）如何在数轴上表示分数？

（4）思考：是否每一个有理数都可以用数轴上的一个点来表示？

概念的学习需要通过4要素来进行加深和巩固（名称、定义、示例、属性），4者缺一不可。通过本环节，学生可以进行结论的归纳：原点表示数0，正数位于原点右侧，负数在原点左侧。

【动手练习】

同学们，请建立数轴，将下列这些数在数轴上表示出来：

（让一名学生在黑板上进行板演，其他学生思考注意点。）

在上题做题过程中，学生应该要注意以下几点：

（1）建立数轴，注意3要素缺一不可；

（2）找准位置，确定对应的数；

（3）进行描点，将数也进行相应的表示。（实心圆点、标记在上方。）

思路提升：数→点（形）。

例：观察下图，A、B、C、D这4个点分别表示什么数?

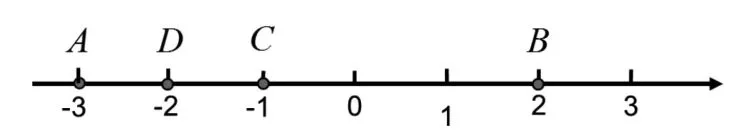
思考：数轴上每一个点与有理数是否构成一一对应的关系？我们能否可以这样来理解：有理数能够填满整个数轴吗？

思路提升：点（形）→数。

环节4：剖析概念进行有理数的大小比较。

【议一议】

观察下面的温度计，建立相应的数轴，同学们，请思考：数轴上面左右两个点之间的大小如何进行标识呢？说说原因。

（教师引导学生类比温度计上的刻度来进行有理数的大小比较。）

引导学生归纳：（1）数轴上两个点表示的数中，右边的点表示的数大；

（2）0作为分界点，正数大于0，负数小于0，正数大于负数。

三、设计说明与教学反思

1.注重教学过程的活动性。

这节课的教学设计是围绕“数轴”这一知识点来展开教学的，通过数学情境的创设和若干具体问题的逐步展开，让学生首先了解什么是数轴，数轴有什么作用，再通过类比归纳并进行动手操作，形成了数轴的相关概念。在教学设计的过程中，教师组织学生以不同形式的活动线索展开研究过程，以问题为主线，让学生通过观察与比较得到数轴的概念，学生自己画出数轴，暴露问题，教师协助进行纠正，由此加深学生对数轴3要素的认识。在数学活动展开时，学生通过数轴来表示有理数，需要将正数、负数、零及整数、分数的表示分别进行思考和分析，从而在自己心中产生对数的再理解和体验，这样既渗透了分类讨论的思想，也能够让学生更加得心应手地解决数学问题。

2.教学过程指向学生思维的发展，注重思想方法的提炼。

本课涉及数形结合的数学思想的萌芽，表现在数轴上的点与有理数之间建立联系；另外，数轴又将所学的数进行直观的分类（正数、零、负数），这里也体现了分类讨论的思想。数轴的概念是引导学生对于数轴3要素的理解，在教学中，教师应当着重对为何要引入数轴进行分析和引导，自然地形成数轴的概念：一方面通过实际问题和创设的情境，引发学生探究数轴概念的兴趣；另一方面不妨多发挥学生学习的主动性和创造性，让他们自己发现和认识到学习数轴的重要价值。值得注意的是，教师在引导学生进行有理数的分类时，需要指出数轴上的点与有理数并非一一对应的关系，还有一类数——无限不循环小数同样也可以在数轴上进行表示的。

3.数学的概念教学应深入到对本质的挖掘之中。

数学课堂的教学任务在于向学生传授知识、启迪思维，将学习所得的知识应用到实际生活中去解决实际问题。从宏观的角度来认识，数轴作为初中数学教学的重要概念，是本章进行相反数学习、绝对值理解、有理数运算等内容的基础和依据；数轴的一个作用是可以对所学的数进行分类，让学生更直观具体地认识到正数、零、负数的区分方法，有利于对于有理数进行精准地分类和比较，从而更方便地认识数的区别和联系。从教学的微观而言，本节课设计的一些探索性问题，为学生创设了良好的探索情境，教师通过这些教学活动，可以使学生的创新思维和归纳能力都有提升，更重要的是，能让学生把所学的数轴知识应用于日常生活之中，从而加深对数学概念的理解和认识，体会其中的数学味道。从教学设计的完整过程来看，数轴一课突出了概念教学的常规思路，即从具体问题过渡到抽象理解，通过类比、归纳来形成数轴概念的同时，注重对概念内涵的探究及概念的辨析。

（作者为江苏省无锡市金星中学教师）