依标据本 凸显四基——以“四基”为核心的一道中考试题的命制与思考

徐建兵

（浙江省衢州市衢江区杜泽镇初级中学）

依标据本 凸显四基
——以“四基”为核心的一道中考试题的命制与思考

徐建兵

（浙江省衢州市衢江区杜泽镇初级中学）

文章围绕着2016年浙江省衢州市中考第22题，从命题思考与阅卷情况等方面呈现了中考试题对课堂教学的导向性作用，揭示课堂教学应注重“四基”，重视对教材的研究开发，重视知识间的相互联系，重视学生思维与能力的培养.

中考试题；课堂教学；四基；数形结合

《义务教育数学课程标准（2011年版）》（以下简称《标准》）把“双基”修改成“四基”，在原有的“基础知识”和“基本技能”的前提下增加了“基本思想”和“基本活动经验”.各地中考命题都非常重视对“四基”的考查，纷纷呈现依据《标准》回归教材的趋势，很多题目源于教材，高于教材，体现背景公平的同时，引导教师重视对教材的研究和开发.笔者有幸经历了2016年浙江省衢州市中考试题的命制、磨题和阅卷的全过程，在此以第22题为例与大家一起分享.

一、源题

利用二次函数的图象求方程x2+x-1=0的解（或近似解）.

解：设y=x2+x-1，

则方程x2+x-1=0的解就是该函数图象与x轴交点的横坐标.

如图1，在直角坐标系中画出函数y=x2+x-1的图象，得到与x轴的交点A，B.

则点A，B的横坐标 x1，x2就是方程的解.

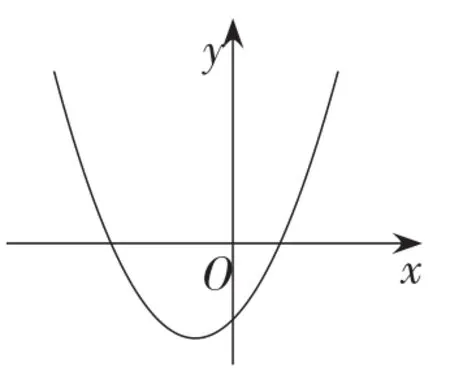
图1

观察图象得到点A的横坐标x1≈0.6，点B的横坐标x2≈-1.6.

所以方程 x2+x-1=0的近似解为 x1≈0.6，x2≈-1.6.

【思考】此题是浙教版《义务教育教科书·数学》九年级上册第一章“二次函数”第四节“二次函数的应用”的例5，题目要求利用二次函数的图象求方程x2+x-1=0的解，体现了数形结合思想中的以形助数，把直观图形数量化，把一元二次方程与二次函数知识有机地融合在一起，是函数思想在方程中的一类应用.

二、试题呈现

例 （2016年浙江·衢州卷第22题）（10分）已知二次函数y=x2+x的图象如图2所示.

（1）根据方程的根与函数图象之间的关系，将方程x2+x=1的根在图上近似地表示出来（描点），并观察图象，写出方程x2+x=1的根（精确到0.1）.

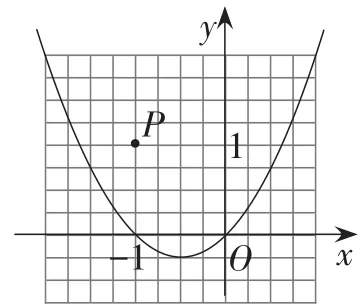
图2

（3）设点P是坐标平面上一点.试选择一种适当的平移方法，使平移后二次函数图象的顶点落在点P上，写出平移后二次函数图象的函数表达式，并判断点P是否在函数的图象上，试说明理由.

【思考】结合2016年的考试说明中二次函数板块的第（6）条考点：会利用二次函数的图象求一元二次方程的近似解，考试要求是b级，根据本卷的知识结构与特点，命题组对此题进行研究拓展，放置在第22题的位置.此题定位在考查数形结合思想，以及“四基”在课堂教学中的落实，把函数、不等式和方程等知识围绕着函数图象进行编制.

三、评分标准

解：（1）描点. …………2分

x1≈-1.6，x2≈0.6. …………1分

（2）画直线. …………1分

x＜-1.5或x＞1. …………2分

平移后表达式为y=x2+2x+2. …………1分

四、命题思考

1.第（1）小题命题思考

把方程x2+x-1=0中的常数项“-1”移到方程的右边得方程x2+x=1，再根据方程的根与函数图象之间的关系求解，这样会使解决问题的方法更加的多样化.

方法1：利用函数值求方程解.

把方程x2+x=1的解看成是二次函数y=x2+x的函数值y=1时横坐标的值.如图3，作直线y=1，与二次函数y=x2+x交于两点，分别过这两点作x轴的垂线，交x轴于两点，这两点的横坐标即为方程x2+x=1的解.

图3

方法2：利用两个函数图象的交点求方程的解.

把方程x2+x=1的解看成是抛物线y=x2+x与直线y=1两个函数图象的两个交点的横坐标.用这种方法还可以解决类似于的二次分式方程的解.

方法3：利用平移改变函数图象与x轴交点求方程的解.

把方程x2+x=1进行移项，得x2+x-1=0.把方程的解看成是函数y=x2+x-1与x轴交点的横坐标的值.考虑到学生在考试时作二次函数的图象费时又很难做标准，预计在求解时会出现很大的偏差，因此命题组给出了网格和二次函数y=x2+x的图象，以便学生解题，因此用方法3解决这一问题时就要用到图形的平移，把二次函数y=x2+x的图象向下平移1个单位长度，或是把平面直角坐标系向上平移1个单位长度，得到二次函数y=x2+x-1的图象，该图象与x轴的交点的横坐标即为方程的根.

2.第（2）小题命题思考

相对二次函数的作图，一次函数的图象要简单得多，而且误差会很小.因此，此题在放弃二次函数图象作图的同时设置了“在同一坐标系中画出一次函数的图象”的问题，所选的这个一次函数是经过多个格点的，这方便了学生标准作图，减少看图求解时的误差，一次函数，则图象的斜率就是.因此，画图时只要利用格点上的点作图，图象将会很标准.直线与二次函数y=x2+x有两个交点，命题组讨论后给出了“观察图象写出当x在什么范围内时，一次函数的值小于二次函数的值”这一问题，初稿是让学生“写出当x在什么范围内时，不等式成立”.为了降低难度，对设问进行了修改，改成了“写出当x在什么范围内时，一次函数的值小于二次函数的值”.同时防止学生去解不等式，在成题时加进了“观察图象”四个字.

3.第（3）小题命题思考

浙教版《义务教育教科书·数学》九年级上册第一章二次函数在学习和研究二次函数的图象与性质时，是从特殊到一般，由简单到复杂，先由y=ax2到，再到，二次函数的平移是其图象与性质的源头，是数形结合的又一大板块，本章中有两个课时研究学习二次函数图象的平移，因此命题组设置了第（3）小题“设点P是坐标平面上一点.试选择一种适当的平移方法，使平移后二次函数图象的顶点落在点P上，写出平移后二次函数图象的函数表达式”.为了使三个问题融为一体，命题组在第（3）小题中添加了“并判断点P是否在函数的图象上，说明理由”.二次函数图象的平移很直观，学生可以用单位长度来表述平移过程，向左移个单位长度，向上移个单位长度.在求平移后解析式时，可以根据平移后的顶点求得平移后解析式为，也可以根据向左移个单位长度，向上移个单位长度得平移后解析式.

五、典型问题

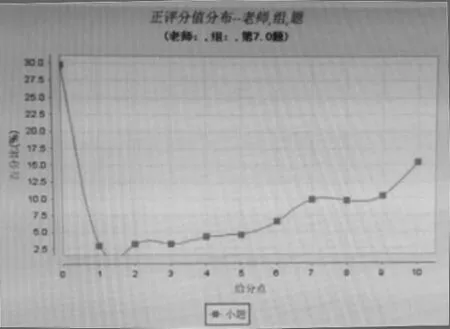
图4

如图4，是此题阅卷后正评分值分布曲线统计图，此题难度不大，但学生的失分严重，充分反映了课堂教学中“四基”落实的不到位，学生基础知识不扎实，基本技能掌握不到位，基本思想难以应用，缺乏操作与解题等活动经验，值得广大教师反思.

1.数形结合思想运用不到位

此题有近30%的学生得0分，说明这些学生不理解利用图象求根这种以形助数的数形结合思想，可以说很大程度上说明了二次函数第四节二次函数的应用的例5教学的失败.在第（1）小题中，有许多学生是先进行解方程，利用求根公式求出方程的解再进行描点.反映学生思维呆板，创新意识不够，在此题中以形助数描点求解体现了处理问题的多样化，体现了一种创新思维与能力.

2.基础知识不扎实，思维不严密

第（2）小题答题中有的写成“1＜x＜-1.5”“-1.5＜x＜1”和“x＜-1.5，且x＞1”等错误形式，可以看出学生对于不等式的正确表示存在缺陷，难以把图象中的大小关系用代数的方式来表示.在第（1）小题中有学生描点正确，但在写方程的解时，把-1.6写成1.6，在长度与坐标的转化时忘记符号，体现了学生思维的不严密性，此问题在第（2）小题答题时也出现把“x＜-1.5”写成“x＜1.5”的情况.

3.学生动手能力较弱，活动经验不足

答卷中有学生在画直线时只画出一个交点，导致写范围时只写出了一部分而出错；有的学生在取点画一次函数时，存在找的不是格点上的点，而且这两个点很近，导致画出的图象误差特别大；还有部分学生利用解方程去求两个函数值相等时x的值，而不是直接看出交点的坐标写出不等式，花费了很多时间求解.第（3）小题答题中部分学生存在格子与单位长度相混淆与格子数错等原因导致平移后解析式求错等等.这些都反映学生活动经验不足，操作能力的不强.

六、题后思考

“双基”从1953年提出到1956年写出之后，一直成为中国数学教育的核心.“基础知识”和“基本技能”功不可没，使得中国数学基础教育在世界上影响很大，但是我们缺少了创造性的东西.因此，《标准》把“双基”改成“四基”，增加了“基本思想”“基本活动经验”.此题难度不大、得分不高，它把方程、函数与不等式紧紧围绕着图象进行展开，分别从方程与函数图象、不等式与函数图象（或不等式与方程）和图形的平移这几个角度进行设问，在体现数形结合基本思想的同时把基础知识与基本技能和活动经验融入其中.例如，利用二次函数图象求一元二次方程的解、根据函数值的大小关系写出自变量的取值范围、方程（组）的解与图象的交点关系、作图求解操作技巧、图象的平移等等.在第（2）小题不等式与函数图象之间的关系中，虽然一元二次不等式没有学过，但利用这种方法同样可以求出不等式的解，这种用已有知识解决未知领域的能力也是学生自主学习和创新能力的一个重要体现.不等式问题有时也可以利用等式进行求解，再根据函数图象写出不等式的解集.第（3）小题图象的平移可以利用对应点的平移来描述和解决，也可以从函数关系式的变化规律中求得，方法的多样性让不同思维的学生得到了不同的展示.判断点是否在图象上的方法是把点代入解析式，看等式是否成立，把方程的解和函数的变量值有机的融为一体.中考的命题导向着教学，因此此题对于我们的课堂教学有着非常重要的意义，引导教师注重“四基”，重视对教材的研究开发，重视知识间的相互联系，重视学生思维与能力的培养.

［1］陈洪远.一道由教材例题改编的中考题［J］.中国数学教育（初中版），2012（3）：40-44.

［2］徐金英，胡兴余.挖掘教材中例、习题的教学功能［J］.中国数学教育（初中版），2009（12）：40-42.

［3］纪尧兵.引导探究考题优化思维品质［J］.中学数学，2013（1）：44-45.

［4］陈德前.一道源自课本的中考综合题［J］.初中生世界（九年级），2014（10）：64-66.

2017—06—27

徐建兵（1978—），男，中学一级教师，主要从事课堂教学改革与命题研究.