一道普通习题的多解多变

魏 创，黄道全

（重庆市凤鸣山中学；重庆市巫溪县天宝初级中学）

一道普通习题的多解多变

魏 创，黄道全

（重庆市凤鸣山中学；重庆市巫溪县天宝初级中学）

培养学生的解题能力是初中数学教学中的一项重要任务，而解题能力重在学生解题方法的探究，让学生学会举一反三和触类旁通才是初中数学学习的真谛.从一道初中数学教材习题的多种解答方法和多种形式的变化出发，对教材习题进行纵向或横向的展开，加强学生对诸多知识和多种方法的理解和变通，最大限度地发挥教材中习题的潜在功能，达到培养学生良好思维方式和创新意识的目的.

深度挖掘；横纵展开；创新思维

笔者在复习九年级四边形这一章时，看到了人教版《义务教育教科书·数学》八年级下册第69页第14题.它是一道几何证明题，从学生的解答中有了很多惊奇的发现.下面阐述一下笔者的经历.

一、原题呈现

如图1，四边形ABCD是正方形，E是边BC的中点.∠AEF=90°，且EF交正方形外角的平分线CF于点F.求证：AE=EF.

在学生的解答和笔者的分析中，共有四种解题方法.

图1

方法1：全等法

如图2，取AB的中点M，连接EM.

由E是BC的中点，就可以得出AM=EC.

由角平分线的性质及等腰直角三角形的性质，就可以得出∠AME=∠ECF.

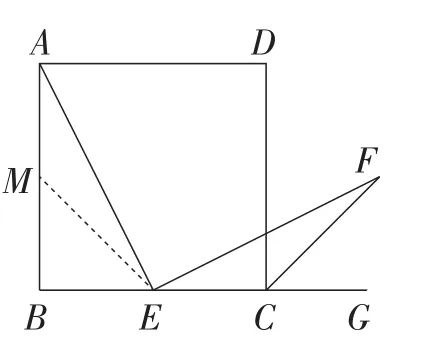
图2

由∠AEF=90°，就可以得出∠BAE=∠CEF.

从而得出△AME≌△ECF，便可以得出结论AE=EF.

【点评】作AB的中点M，构造等腰直角三角形，根据正方形的性质，证明△AME≌△ECF，由全等三角形的性质就可以得出结论.我们把这种解法称为自然解法，是大部分学生普遍运用的解法，有90%的学生使用此种方法解答.

方法2：相似法

如图3，过点F作FH⊥BG于点H，

设BE=CE=m，CH=n，

由正方形的性质，可得△ABE∽△EHF.

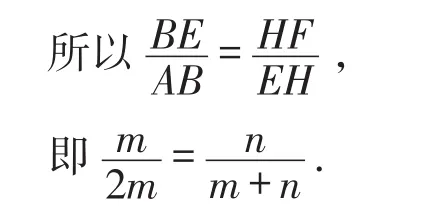
图3

所以m=n，

即BE=HF.

所以可证△ABE≌△EHF.

进而得出结论AE=EF.

【点评】过点F作BG的垂线，证明△ABE∽△EHF，由相似三角形的性质求出BE=HF，这是解答的关键，再证明△ABE≌△EHF就可以得出结论.由题先证得BE=EH是难点.

方法3：函数法

如图4，将正方形ABCD放到平面直角坐标系中，点B与原点O重合，点A在y轴上，点C在x轴上，

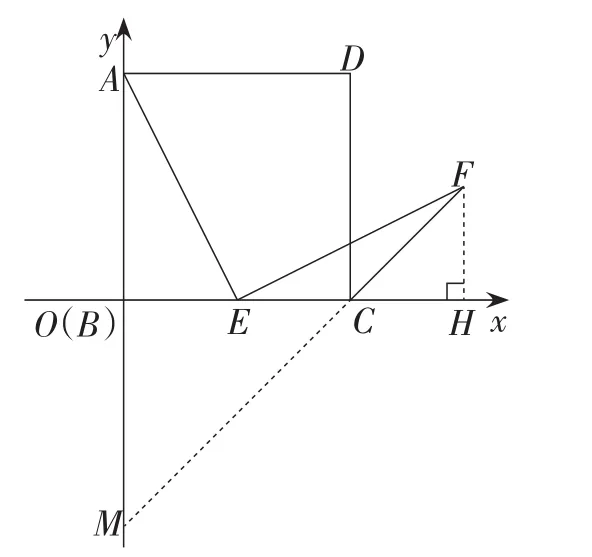
图4

设BE=CE=m，

则AB=2m.

所以点A（0，2m），C（2m，0），E（m，0）.

设直线AE的解析式为yAE=k1x+b1，直线EF的解析式为yEF=k2x+b2，直线CF的解析式为yCF=k3x+b3，

由∠AEF=90°，得AE⊥EF.

所以k1k2=-1.

将点E的坐标带入解析式为yEF=k2x+b2，就可以求出.

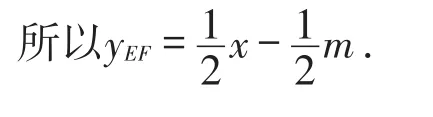
延长FC交y轴于点M，可得BM=BC=2m.

所以M（0，-2m）.

由待定系数法，可求得yCF=x-2m.

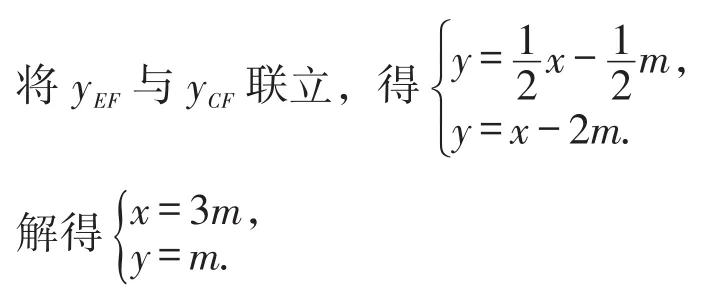
所以BH=3m，FH=m.

所以EH=2m.

从而可以得出结论AE=EF.

【点评】建立平面直角坐标系，表示出各关键点的坐标，由待定系数法求出直线AE，EF和CF的解析式，由勾股定理求出AE和EF的值，从而得出结论.这种解法比较大胆和新颖，但是比较复杂.

方法4：四点共圆法

如图5，连接AF，AC，

容易得出∠ACB=45°，∠ACF=90°.

由∠AEF=90°，就可以得出A，E，C，F四点共圆.

所以∠AFE=∠ACB=45°.

所以∠AFE=∠EAF.

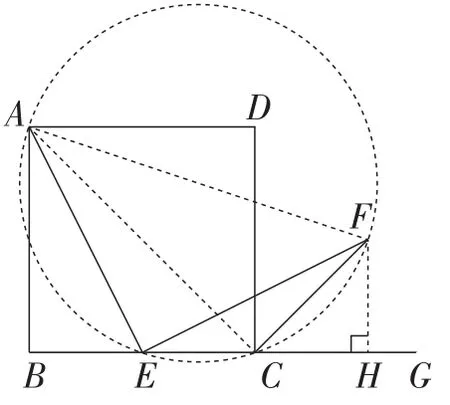
图5

从而得出结论AE=EF.

【点评】这种证明方法让人眼前一亮，思维独特、新颖，过程简洁、明了，但不容易想到.它无疑是几种证明方法中一种比较独特的好方法.如何想到这样证明呢？仔细审题，连接AC，易发现∠ACF=90°，就有E，C，F，A四点共圆，进而可以得出∠EAF=∠EFA，从而得出结论.

二、动态变化一

如果把E是边BC的中点改为点E是边BC上（除点B，C外）的任意一点，其他条件不变，结论AE=EF仍然成立.

如图6，在AB上取一点M，使得AM=EC，连接ME.

可以得出BM=BE.

所以∠BME=45°.

所以∠AME=135°.

由CF是外角平分线，

得∠DCF=45°.

所以∠ECF=135°.

所以∠AME=∠ECF.

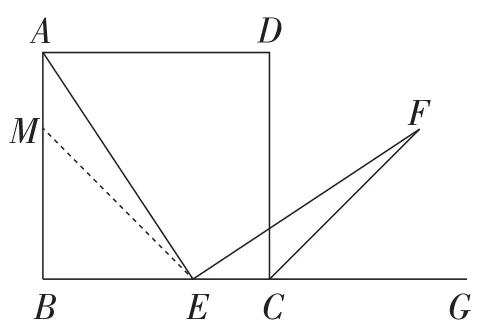
图6

由 ∠AEB+∠BAE=90°， ∠AEB+∠CEF=90°，可以得出∠BAE=∠CEF.

由ASA就可以证得△AME≌△ECF.

从而得出结论AE=EF.

同样，也可以过点F作FH⊥BG于点H，类比图3，用相似的方法证明.

如图7，设AB=a，BE=m，CH=FH=n，

所以EH=a-m+n.

由题易证△ABE∽△EHF.

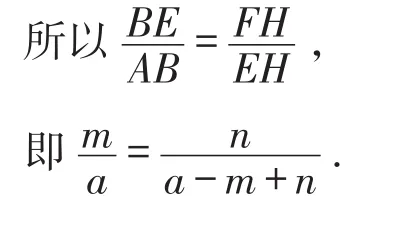
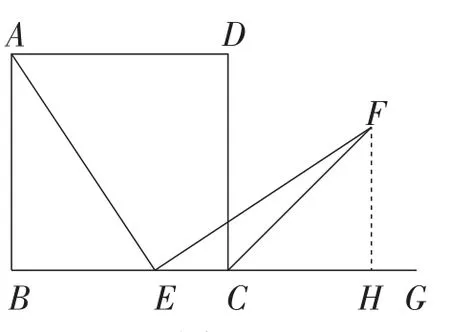
图7

所以an=am-m2+mn.

整理，得am-m2+mn-an=0.

进而得出（m-n）（a-m）=0.

因为a-m≠0，

所以m=n.

所以EH=a.

所以AB=EH.

进而由AAS得证△ABE≌△EHF.

从而得出结论AE=EF.

此种位置情况通过观察比较，同样可以在直角坐标系中运用一次函数求解.

如图8，设AB=BC=a，BE=m，延长FC交y轴于点M，

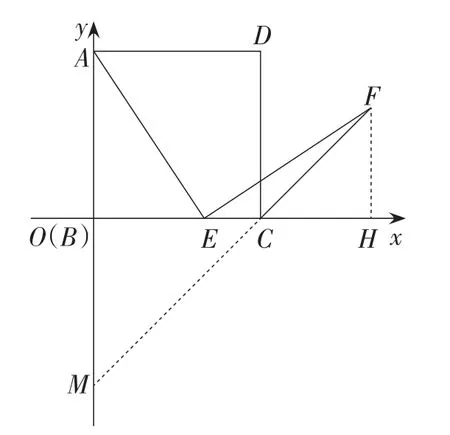
图8

可以得出BM=BC=a.

所以点A（0，a），C（a，0），E（m，0），M（0，-a）.

设直线AE的解析式为yAE=k1x+b1，直线EF的解析式为yEF=k2x+b2，直线CF的解析式为yCF=k3x+b3，

由k1k2=-1，求出.

再求出yCF=x-a.

将yCF与yEF联立，求出

所以F（a+m，m）.

所以FH=m，EH=a.

从而得出结论AE=EF.

用四点共圆定理求解.

如图9，连接AF，AC，

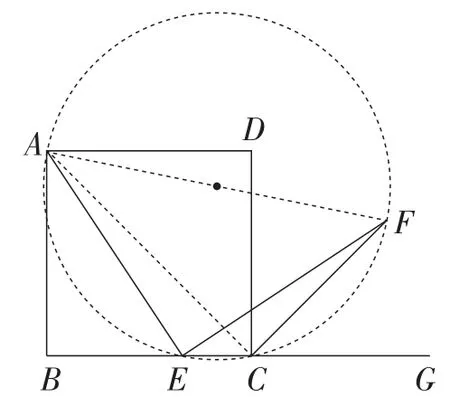
图9

很容易得出∠ACB=45°，∠ACF=90°.

由∠AEF=90°就可以得出A，E，C，F四点共圆.

所以∠AFE=∠ACB=45°.

所以∠EAF=45°.

所以∠AFE=∠EAF.

从而得出结论AE=EF.

三、动态变化二

当点E是BC的延长线上任意一点时，点E不与点C重合，其他条件不变，结论AE=EF也是成立的.

如图10，在BA的延长线上取一点M，使AM=CE，连接EM，

图10

由AB=BC就可以得出BM=BE.

进而得出∠M=45°.

由CF是外角∠DCG的平分线，得出∠GCF=45°.

得出∠M=∠GCF.

由AD∥BC就可以得出∠DAE=∠CEA.

由∠MAD=∠AEF=90°就可以得出∠MAE=∠CEF.

由ASA可以得出△MAE≌△CEF.

进而得出结论AE=EF.

同样可以用以上的另外三种方法证明结论.

如图11，过点F作FH⊥BG于点H，

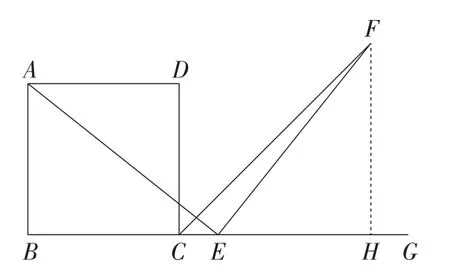
图11

设AB=a，BE=m，CH=FH=n，

则EH=n-m+a.

由题可证△ABE∽△EHF.

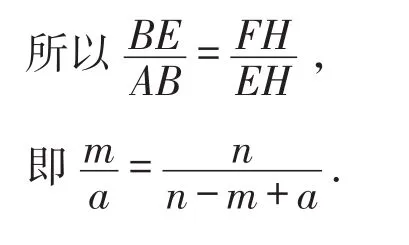
所以an=nm-m2+am.

进而得出（n-m）（m-a）=0.

由于m-a≠0，

所以m=n，

即BE=FH.

进而由AAS证得△ABE≌△EHF.

从而得出结论AE=EF.

如图12，连接AF，AC，

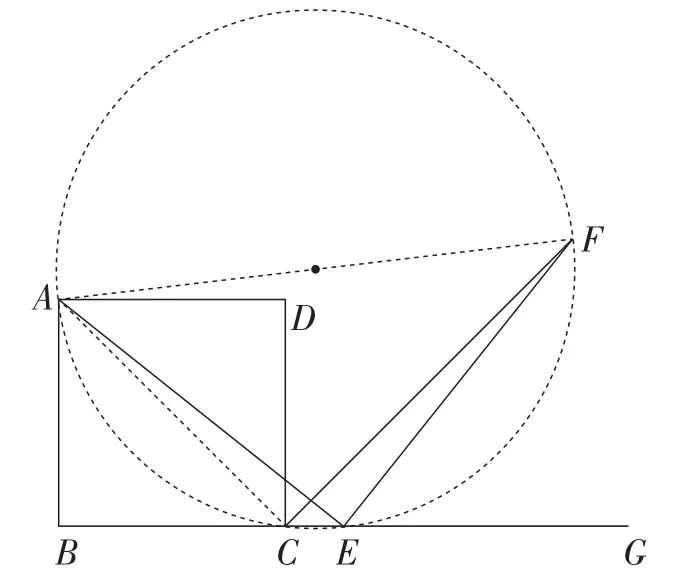
图12

很容易得出∠ACB=45°，∠ACF=90°.

由∠AEF=90°就可以得出A，E，C，F四点共圆.

由圆的内接四边形的一个外角等于内对角可得出∠AFE= ∠ACB=45°.

所以∠EAF=45°.

所以∠AFE=∠EAF.

从而得出结论AE=EF.

图13的解法与图8相同，略.

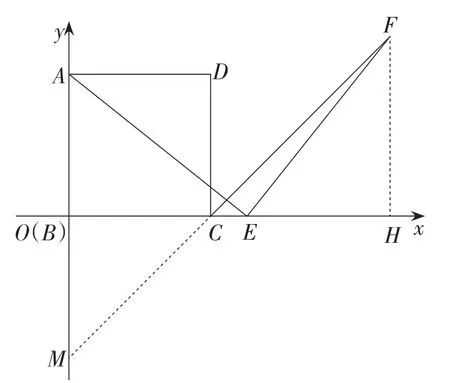
图13

四、动态变化三

根据前面的变化，笔者思考，那么当点E是CB的延长线上任意一点时，点E不与点B重合，其他条件不变，AE=EF还成立吗？原题的四种解题方法仍然适用吗？通过作图分析，AE=EF是成立的，四种解题方法同样适用.

方法1：如图14，延长AB至点M，使AM=EC，连接EM.

由等式的性质就可以得出BE=BM.

由∠EBM=90°，就可以得出∠M=45°.

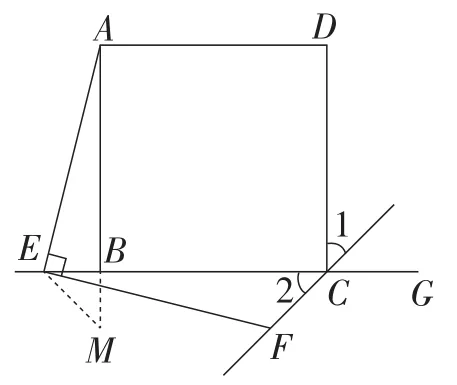
图14

由题可知∠2=∠1=45°.

进而得出∠M=∠2.

由题易得∠EAB=∠FEC.

由ASA就可以得出△AEM≌△EFC.

从而得出结论AE=EF.

方法2：如图15，过点F作FH⊥BG于点H，

设AB=a，BE=m，CH=FH=n，

则EH=m+a-n.

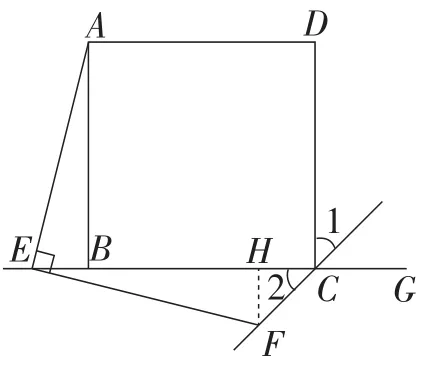
图15

所以an=m2+am-mn.

进而得出（m-n）（m+a）=0.

由于m+a≠0，

所以m=n，

即BE=FH.

进而由AAS证得△ABE≌△EHF.

从而得出结论AE=EF.

方法3：如图16，设AB=BC=a，BE=m，

FC交y轴于点M，可以得出BM=BC=a.

所以点A（0，a），C（a，0），E（-m，0），M（0，-a）.

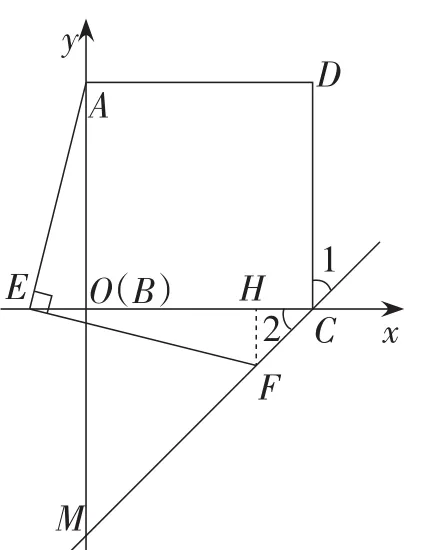
图16

设直线AE的解析式为yAE=k1x+b1，直线EF的解析式为yEF=k2x+b2，直线CF的解析式为yCF=k3x+b3，

由k1k2=-1，得.

再求出yCF=x-a.

将yCF与yEF联立方程组求出

所以F（a-m，-m）.

所以FH=m，EH=a.

从而得出结论AE=EF.

方法4：如图17，连接AF，AC，

很容易得出∠2=45°，∠ACF=90°.

再由∠AEF=90°就可以得出A，E，C，F四点共圆.

所以∠EFA=∠2=45°.

所以∠EAF=45°.

所以∠EAF=∠AFE.

从而得出结论AE=EF.

图17

五、解题启示

通过以上四种变化情况的解答，不难发现此题的点E在直线BC上移动时（不与点B，C重合），其他条件不变，而AE=EF恒成立，并且四种解法均可用.几何动点问题是中考必考问题，也是难点问题，动中求静，找到在变化的过程中的不变量是解决问题的关键.

作为教材的一道普通习题，可运用多种不同的方法进行解答，这是对习题横向研究的结果；将普通的习题实施不同形式的多种变化，这是对习题的纵向渗透.对于大多数的解答者而言，谁也不知道是怎么想出这种解法的.这实际是知识同化的结果.

教材中类似这样的例题、习题并不鲜见.但是真正能对这些习题进行纵向或横向的展开，需要施教者做出百倍的努力和探索，使之成为一种习惯，便能加强学生对诸多知识和多种方法的理解和变通，从而最大限度地发挥教材中习题、例题的潜在功能，从而达到培养学生良好思维方式和创新意识的目的.

［1］张庆华.中考科学集训［M］.沈阳：白山出版社，2008.

［2］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2017—06—11

魏创（1976—），男，中学一级教师，主要从事初中数学教育教学研究.