一道数学题的一题多变——深化价值引领，凸显数学思考

白金强

（河北省高碑店市教师发展中心）

一道数学题的一题多变
——深化价值引领，凸显数学思考

白金强

（河北省高碑店市教师发展中心）

一题多解强调多角度审视问题；一题多变则强调对原题的题干和结论的不断变化进行的深层次探索，两者的有机结合对培养学生的创造性思维和发散性思维有重要的作用.从一道题目的多种解法出发，通过不断改变习题的条件，进一步挖掘习题的思维价值，达到深化价值引领，凸显数学思考.

价值引领；一题多解；一题多变

一题多解强调从多角度审视和分析问题，对开发解题潜能，提高解决综合问题的能力有很重要的作用.而一题多变则可以使学生克服思维定势的影响，不局限于某一方面的思考，多角度、多方位地创设问题、解决问题，它有利于培养学生的数学思维和创新意识.一题多变强调不能仅仅停留在对原习题的解法探索上，而应适当地、有机地对原习题的题干和结论进行深层次的探索，把解题方法迁移到新的情境中.

数学家波利亚认为，一个有责任心的教师与其穷于应付烦琐的数学内容和过量的题目，还不如适当选择某些有意义但又不太复杂的题目去帮助学生挖掘题目的各个方面，在指导学生解题的过程中，提高他们的才智与推理能力.前苏联数学教育家奥加涅相在《中学数学教学法》中也指出，必须重视很多习题潜存着进一步扩展其数学功能、发展功能和教育功能的可能性……

下面笔者以一道习题为例，探索如何从一题多解到一题多变，培养学生学会从多层次、广视角、全方位地认识、研究问题，以及创新意识和创新能力.

原题：如图1，点O将线段DA平分，分别以OD，OA为边在线段DA的同侧作等边三角形OCD和等边三角形AOB，连接AC，DB，这两条线段交于点E，连接CB，求∠AEB.

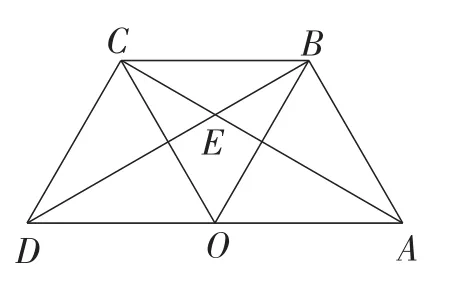
图1

针对这道题笔者总结出了三种解题思路，即分别是应用三角形全等知识、四边形相关知识、圆相关知识，其中运用圆相关知识解答最简捷.

一道数学题，由于思考的角度不同可以得到多种不同的解法，寻求多种解法，有助于拓宽解题思路，发展观察、想象、探索及思维能力.而通过变化则可以进一步深化试题的价值引领，凸显数学思考，一题多变则是课堂教学应当予以关注的重要一点.

首先从题目中的条件变化开始，思考特殊的条件，能不能不取特殊点呢？且看下面几种变化情形.

一、分点改变，三角形不变

如图2，点O为DA上任意一点（O不再是DA的中点），以OD，OA为边在DA同侧分别作等边三角形OCD和等边三角形AOB，连接AC，DB，这两条线段交于点E，连接CB，求∠AEB.

解：因为△OCD和△OAB均为等边三角形，

所以可证明△DOB≌△COA.

所以∠DBO=∠CAO.

所以∠AEB=∠BOA=∠COD=60°.

图2

二、分点不变，三角形改变

1.顶角相等的等腰三角形

如图3，O为DA中点，分别以OD，OA为腰在线段DA的同侧作等腰三角形OCD和等腰三角形AOB，∠DOC=∠AOB，连接AC，DB，这两条线段交于点E，连接CB，求∠AEB，∠COD和∠AOB之间的关系.

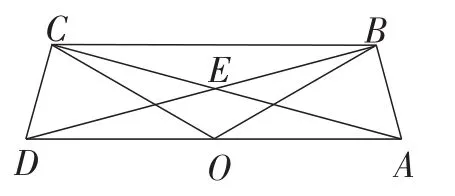
图3

解：（方法1） 由OD=OC，OB=OA，∠DOC=∠AOB，可证△BOD≌△AOC.

所以∠DBO=∠CAO.

所以∠AEB=∠AOB=∠COD.

（方法2）以点O为圆心作圆，运用圆内角和圆心角有关知识也能简捷求解.

这时所求∠AEB为两个等腰三角形顶角度数和的一半.

2.顶角不相等的等腰三角形

如图4，点O将线段DA平分，分别以OD，OA为腰在线段DA的同侧作等腰三角形OCD和等腰三角形AOB，连接AC，DB，这两条线段交于点E连 接CB， 求 ∠AEB， ∠COD 和∠AOB之间的关系.

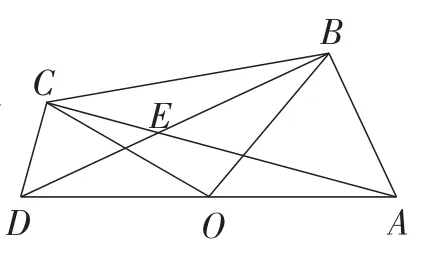
图4

解：以点O为圆心，OD为半径作圆，则利用圆内角和圆心角的定义可求出∠AEB=∠ACB+∠CBD=.

这时所求∠AEB依然为两个等腰三角形顶角度数和的一半.

三、分点、三角形均改变

1.分点任意，顶角相等的等腰三角形

如图5，点O为DA上任意一点，分别以OD，OA为腰在线段DA的同侧作等腰三角形OCD和等腰三角形AOB，∠DOC=∠AOB，连接AC，DB，这两条线段交于点E，连接CB，求∠AEB，∠COD和∠AOB之间的关系.

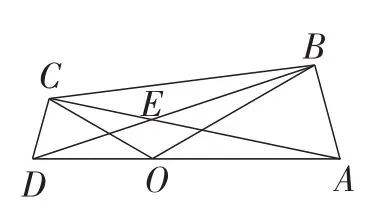
图5

解：由OD=OC，OB=OA，∠DOC=∠AOB，可证△BOD≌△AOC.

所以∠DBO=∠CAO.

所以∠AEB=∠AOB=∠COD.

所求∠AEB依然为两个等腰三角形顶角度数和的一半.

2.分点任意，两个相似三角形

如图6，点O为DA上任意一点，满足△DOC∽△BOA，连接AC，DB，这两条线段交于点E，连接CB，求∠AEB，∠COD和∠AOB之间的关系.

图6

又因为∠COD=∠AOB，

所以∠DOB=∠COA.

所以△DOB∽△COA.

所以∠ACO=∠ADE.

而 ∠AEB= ∠ADE+ ∠DAC， ∠COD= ∠DAC+∠ACO，

所以∠AEB=∠COD=∠AOB.

（方法2）由△DOC∽△BOA，可证点A，B，C，D共圆，继而很容易求解.

这时所求∠AEB为两个相似三角形有公共顶点的角的度数和的一半.

以上研究都是围绕线段DA和分点展开，如果将三角形落在线段DA边上的两条边，顶点不变分别向上旋转，结论是否还成立呢？

四、OC，OA不在同一条直线上的情形

1.等边三角形不变，OA，OB不再共线

如图7，△AOD和△OBC为等边三角形，OA=OB，且OA，OB不在同一线段上，求∠BEC，∠DOA和∠BOC之间的关系.

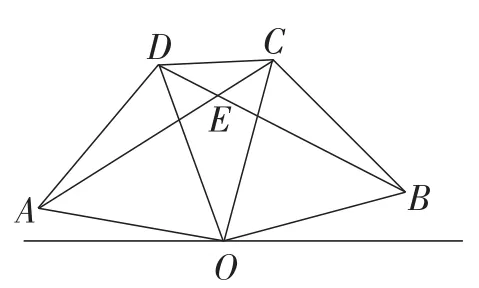
图7

解：以点O为圆心，OA为半径作圆，运用圆的有关知识不难求出∠BEC.

2.等腰三角形，OA，OB不再共线

如图8，△AOD和△OBC为等腰三角形，OA=OD=OC=OB，且OA，OB不在同一线段上，求∠BEC.

图8

解：以点O为圆心，OA为半径作圆，同样运用圆的有关知识不难求出∠BEC.

借助几何画板软件这个工具可以把“两个三角形在DA的同侧”这个条件通过旋转改变为不在同侧，符合前面条件的结论依然成立（有兴趣的读者可自行研究，限于篇幅，本文不再赘述）.

笔者以为，一道好的数学题的价值不只是体现在有多少种方法能求解，哪种方法简捷上，如果只是单纯的、孤立的去解答它，那么再好的解法充其量只不过是解决了一个问题.数学解题的价值在于培养学生从特殊中寻找一般规律的能力，因为一般性往往蕴含在特殊性中，既要重视一题多解，更要关注一题多变，在变中发现问题、引发思考，在思考中深化价值引领.

［1］杨振德.关注价值引领凸显数学思考［J］.基础教育课程，2015（24）：17.

［2］任勇.任勇的中学数学教学主张［M］.北京：中国轻工业出版社，2012.

［3］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2017—06—05

白金强（1967—），男，中学高级教师，主要从事中小学数学教学研究.