矩阵理论在AES中的应用

王志俊 姜咏梅

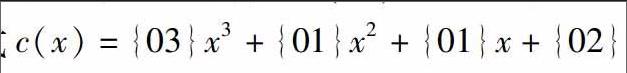
【摘要】矩阵是现代数学中最基本的概念之一.本文从矩阵运算的角度对高级加密标准中的字节代替变换和列混合变换给予解释，说明了字节代替变换是状态数组字节上的仿射变换，列混合变换是状态数组列上的线性变换.

【关键词】矩阵；高级加密标准；仿射变换；线性变换

2001年美国国家标准技术研究所（NIST）正式公布了高级加密标准（AES），并于2002年5月正式生效.AES被认为是没有明显缺点和安全漏洞的，能够抵抗目前已知各种方法攻击的、安全性能良好的密码体制.AES是一种分组密码，分组长度为128 bits，其加密和解密中的每个中间状态也是128 bits.

设s是一个中间状态，将s按从左到右的顺序分为16个字节，然后，将这16个字节排成一个称为状态数组的4阶方阵

一、字节代替变换

字节代替变换是将状态数组中的每个字节通过S盒非线性地变换为另一个字节.在教学过程中如果只简单地通过S盒查表得到字节代替变换的输出，会使部分学生产生一些困惑：这个S盒是如何得到的？为什么会有这样的输出？有了状态数组矩阵，S盒产生输出的过程就可以用矩阵的加法和乘法运算来代替：设a0a1a2a3a4a5a6a7是字节替代变换前状态数组中（i，j）位置的一个字节，并将其看成是有限域GF（28）中的元素，先求出其乘法逆元，不妨假设为b0b1b2b3b4b5b6b7，则在字节替代变换后状态数组中（i，j）位置的结果是通过下面的仿射变换得到的.

这样的解释既能够让学生听懂，揭开S盒的神秘面纱，又可以让学生学习到一个新的数学概念——仿射变换.

二、列混合变换

列混合变換是对状态数组逐列进行变换，它将状态数组中的每一列看作GF（28）上的一个多项式，然后，与多项式 做模x4+1乘法.客观地说，要从这个角度讲清列混合变换是有一定难度的，比如，为什么要与多项式c（x）做乘法，为什么模多项式是x4+1，等等，这需要具有有限域上多项式环、商环等抽象代数的基础.基于这个原因，上面对列混合变换的处理显得比较抽象，由于学习本课程的学生已经具备线性代数的基础，我们可以用简单的矩阵乘法来代替：任意取列混合变换前状态数组的一列，比如，第j列，则列混合变换后状态数组的第j列可以通过下面的矩阵乘法来表示

用上面矩阵乘向量（也可以理解为线性变换）来解释列混合变换比较直观，学生容易接受.当然，这样处理也会产生一个问题：上面两种处理列混合变换的方法是否等价？具体来讲，给定状态数组的一列，用上面两种方法得到的结果是否相同？对此问题我们可以通过下面的计算给出简单的证明.

将所得多项式的系数写成列向量的形式就会发现它恰好可以用上面矩阵的乘法来表示.

三、结束语

现代密码学与代数学（包括线性代数和抽象代数）之间有着紧密的联系，许多密码体制（比如，EIGamal公钥密码体制）的安全性都是基于代数学中的一些问题的难解性.所以，要在现代密码学有深入的研究，离不开坚实的代数学知识.

【参考文献】

[1]林东岱，曹天杰.应用密码学[M].北京：科学出版社，2009：73-82.

[2]陈鲁生，沈世镒.现代密码学[M].北京：科学出版社，2008：58-72.

[3]江龙，程林凤，胡建华，魏琦瑛.线性代数[M].北京：高等教育出版社，2012：21-33.

[4]付丽，丁慧.代数在密码学中的应用[J].通化师范学院学报，2014（35）：29-31.