SEP矩阵的性质

李 金, 王 龙, 魏俊潮

(扬州大学数学科学学院, 江苏 扬州 225002)

1 基本概念及引理

Cn×n表示复数域A上的全矩阵环．设A∈Cn×n, 矩阵A+称为A的Moore-Penrose逆[2]．如果A+是方程A=AXA,X=XAX, (AX)H=AX, (XA)H=XA的解, 则矩阵A称为MP逆．若关于X的方程A=AXA,X=XAX,AX=XA有解, 且解是唯一的, 则称该解为矩阵A的群逆, 记为A#[1]． 若A=AAHA或等价于A+=AH, 则A称为PI矩阵[3]．若A#存在, 且A#=A+, 则称A为EP矩阵[7]．如果群可逆矩阵A既是PI的又是EP的, 则称A为SEP矩阵, 即A#=A+=AH[4-5]．有关EP矩阵、PI矩阵以及SEP矩阵的相关研究, 可见参考文献[8-14]．

引理1[4]设A∈Cn×n, 则A是PI矩阵当且仅当AA+=AAH．

引理2[4]设A∈Cn×n是群可逆矩阵, 则A是SEP矩阵当且仅当AH=A#．

引理3[4]设A∈Cn×n, 则A是SEP矩阵当且仅当A2AH=A．

引理4[15]设A∈Cn×n是群可逆矩阵, 则如下结论成立:

i)A#=A#A+A=AA+A#;

ii)A+=A+(AA#)H=(AA#)HA+;

iii) 这些条件等价: 1)A是EP矩阵; 2)A=A2A+; 3)A=A+A2; 4)A+=A+A+A; 5)A+=AA+A+; 6)AH=AHA+A; 7)AH=AA+AH; 8)AA#=AA+; 9)A#A=A+A; 10) (AA#)H=AA#; 11)A+=A#AA+; 12)AH=AHA#A; 13)A#=A#AA+．

2 主要结论

引理5设A∈Cn×n为群可逆矩阵, 则: i) (A+)#=(AA#)HA(AA#)H; ii) (A#)+=A+A3A+．

证明 i) 设X=(AA#)HA(AA#)H, 易验证

A+(AA#)H=A+AA+(AA#)H=A+(AA#AA+)H=A+(AA+)H=A+AA+=A+,

则根据群逆的定义可知

A+X=A+(AA#)HA(AA#)H=A+A(AA#)H=(AA#A+A)H=(AA#)H．

同理可知,XA+=(AA#)HA(AA#)HA+=(AA#)HAA+=(AA#)H, 故A+X=XA+．进一步可知,A+XA+=A+(AA#)HA(AA#)HA+=(AA#)HA+=A+, 且XA+X=(AA#)HA(AA#)HA+(AA#)H·A(AA#)H=(AA#)H(AA#)HA(AA#)H=(AA#)HA(AA#)H．综上可得,(A+)#=(AA#)HA(AA#)H．

ii) 注意到A#A+A=A#和AA+A#=A#．由Moore-Penrose 逆定义, 直接验证可知A#A+A3A+=AA+,A#A+A3A+A#=AA+A#=A#,A+A3A+A#A+A3A+=A+AA+A3A+=A+A3A+, 故(A#)+=A+A3A+．

引理6设A∈Cn×n为群可逆矩阵, 则A为SEP矩阵当且仅当AHA+(A#)H=A#A+(A+)H．

证明 必要性．由A为SEP矩阵知A#=A+=AH, 有AHA+(A#)H=A#A+A=A#, 且A#A+(A+)H=A#A+A=A#, 故AHA+(A#)H=A#A+(A+)H．

充分性．因AHA+(A#)H=A#A+(A+)HAA+,左乘AA+得AA+AHA+(A#)H=AA+A#A+(A+)H=A#A+(A+)H=AHA+(A#)H, 右乘AH得AA+AHA+=AHA+, 再右乘A(AA#)H得AA+AH=AH．由引理4知A为EP矩阵, 故A#=A+,AA+=A+A, 于是AHA+(A#)H=A#A+(A+)H, 右乘AH有AHA+=A#A+．进一步可知,AH=AHAA+=AHA+A=A#A+A=A#, 所以A为SEP矩阵．

引理7矩阵A为SEP矩阵当且仅当AH也为SEP矩阵．

证明 必要性．若A为SEP矩阵, 则A#=A+=AH, 有(A#)H=(A+)H=A, 从而(AH)#=(AH)+=(AH)H, 故AH为SEP矩阵．

充分性．若AH为SEP矩阵, 由必要性知(AH)H为SEP矩阵, 即A为SEP矩阵．

由引理7知, 可用AH代替引理6中的A可得下面推论．

推论8设A∈Cn×n为群可逆矩阵, 则A为SEP矩阵当且仅当A(A+)HA#=(A#)H(A+)HA+．

引理9设A∈Cn×n为群可逆矩阵, 若A+AH=A+A#, 则A为SEP矩阵．

证明 由题设A+AH=A+A#, 知A+A#=A+AHAA+=A+A#AA+, 左乘A得A#=A#AA+．由引理4知A为EP矩阵, 则AH=A+AAH=AA+AH=AA+A#=A#, 故由引理2知A为SEP矩阵．

引理10设A∈Cn×n为群可逆矩阵, 若A2=(A#)HA, 则A为SEP矩阵．

证明 因为A2=(A#)HA, 左乘A+A得A+A3=(A#)HA=A2,A=A2A#=A+A3A#=A+A2, 由引理4知A为EP矩阵, 则有A=A2A+=(A#)HAA+=(A#)H, 故AH=A#, 因此A为SEP矩阵．

由推论8构造方程

AXA#=(A#)HXA+．

(1)

定理11设A∈Cn×n为群可逆矩阵, 则A为SEP矩阵当且仅当方程(1)在集合ρA中有解, 其中ρA={A,A#,A+,AH, (A#)H,(A+)H,(A+)#,(A#)+}．

证明 必要性．若A为SEP矩阵, 则由推论8知X=(A+)H为一个解．

充分性．1) 若X=A为解, 则A2A#=(A#)HAA+=(A#)H, 即A=(A#)H．取共轭转置, 得AH=A#, 故A为SEP矩阵．

2) 若X=A#, 则A#=AA#A#=(A#)HA#A+=(A#)HA#A+AA+=A#AA+, 由引理4知A为EP矩阵, 故A=A#A2=(A#)HA#A+A2=(A#)HA#A=(A+)H．取共轭转置, 得AH=A+, 故A为SEP矩阵．

3) 若X=A+, 则AA+A#=(A#)HA+A+, 即A#=(A#)HA+A+, 左乘A+A得AA+A#=A#, 由引理4知A为EP矩阵, 于是X=A+=A#, 由2)知A为SEP矩阵．

4) 若X=AH, 则AAHA#=(A#)HAHA+=A+,左乘AA+得A+=AAHA#=AA+A+,由引理4知A为EP矩阵．又因AA+=A+A=AAHA#A=AAHAA#=AAH, 由引理1知A为PI矩阵, 故A为SEP矩阵．

5) 若X=(A+)H, 则A(A+)HA#=(A#)H(A+)HA+, 右乘A得A(A+)H=(A#)H(A+)H．取共轭转置, 得A+AH=A+A#, 由引理9知A为SEP矩阵．

6) 若X=(A#)H, 则A(A#)HA#=(A#)H(A#)HA+, 右乘A+A得(A#)H(A#)HA+=(A#)H·(A#)HA+A+A, 左乘AHAH得A+=A+A+A,由引理4知A为EP矩阵, 故X=(A#)H=(A+)H为解, 由5)知A为SEP矩阵．

7) 若X=(A+)#=(AA#)HA(AA#)H, 则A(AA#)HA(AA#)HA#=(A#)H(AA#)HA(AA#)HA+=(A#)H, 左乘AA+得(A#)H=AA+(A#)H, 取共轭转置得A#=A#AA+, 由引理4知A为EP矩阵, 故X=(A+)#=(A#)#=A, 由1)知A为SEP矩阵．

8) 若X=(A#)+=A+A3A+, 则AA+A3A+A#=(A#)HA+A3A+A+, 右乘AA+得A2A+=A, 由引理4知A为EP矩阵, 故X=A+A3A+=A, 由1)知A为SEP矩阵．

对于方程AXA#=(A#)HXA+, 当A为EP矩阵时, 得AXA#AA+=(A#)HXA+, 故可构造方程

AXA#AY=(A#)HXY．

(2)

下面将利用方程(2)的可解性来刻画SEP矩阵．

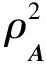
充分性．1) 当Y=A时, 方程(2)转变为

AXA=(A#)HXA,

(3)

则: i)X=A时, 有A3=(A#)HA2, 右乘A#得A2=(A#)HA, 故由引理10知A为SEP矩阵; ii)X=A#时, 有A=(A#)HA#A, 右乘A得A2=(A#)HA, 故A为SEP矩阵; iii)X=A+时,A=AA+A=(A#)HA+A, 左乘AH得AHA=A+A, 由引理1知A为PI矩阵, 有A+=AH=((A#)HA+A)H=A+AA#, 则A为EP矩阵, 故A为SEP矩阵; iv)X=AH时,AAHA=(A#)HAHA, 右乘A+得AAH=(A#)HAH=(AA#)H, 有AA#=(AAH)H=AAH=(AA#)H, 故A为EP矩阵, 于是AAHA=(A+)HAHA=A,则A为PI矩阵, 从而A为SEP矩阵; v)X=(A#)H时,A(A#)HA=(A#)H·(A#)HA,右乘A+得A(A#)H=(A#)H(A#)H, 右乘(AH)3得A(AH)2=AH, 取共轭转置得A=A2AH, 由引理3知A为SEP矩阵; vi)X=(A+)H时,A(A+)HA=(A#)H(A+)HA,右乘A#得A(A+)H=(A#)H(A+)H, 右乘AH得A2A+=(A#)H, 有A#=AA+AH, 于是A+A#=A+AH, 故由引理9知A为SEP矩阵; vii)X=(A+)#=(AA#)HA(AA#)H时, 则易得A(AA#)HA(AA#)HA=(A#)H·(AA#)HA(AA#)HA=(A#)HA(AA#)HA, 右乘A+A+(AH)2得A(AA#)HA(AA#)HAA+A+(AH)2=(A#)HA(AA#)HA+(AH)2=A(AA#)H(AH)2=(A#)H(AH)2=AAHAH=AH,故A为SEP矩阵; viii)X=(A#)+=A+A3A+时, 有A(A+A3A+)A=(A#)HA+A3A+A, 即A3=(A#)HA+A3, 右乘(A#)2得A=(A#)HA+A, 由(iii)可知A为SEP矩阵．

2)Y=A#时, 方程(2)转变为AXA#AA#=(A#)HXA#．该方程右乘A2得方程(3), 由(1)的证明可知A为SEP矩阵．

3)Y=A+时,可得方程

AXA#AA+=(A#)HXA+,

(4)

则: i)X=A时,A2A+=(A#)H, 由1)中(vi)知A为SEP矩阵; ii)X=A#时,AA#A+=(A#)H·A#A+, 右乘A3得A2=(A#)HA, 由引理10知A为SEP矩阵; iii)X=A+时,A#AA+=(A#)H·A+A+, 左乘A+A得A+=A#AA+, 由引理4知A为EP矩阵, 故A#=A#AA+=(A#)HA+A+=(A#)HA#A#, 右乘A3得A2=(A#)HA, 由引理10知A为SEP矩阵; iv)X=AH时,AAHA#AA+=(A#)HAHA+=A+, 右乘A2得AAHA=A+A2, 左乘AA+得A+A2=AA+A+A2, 右乘A#A+得A+=AA+A+, 由引理4知A为EP矩阵, 故AAHA=A+A2=A,即A为PI矩阵, 因而A为SEP矩阵; v)X=(A#)H时,A(A#)HA#AA+=(A#)H(A#)HA+, 左乘A+A得A+A2(A#)HA#AA+=A(A#)HA#AA+,右乘A2A+得A+A2(A#)H=A(A#)H, 取共轭转置得A#AHA+A=A#AH, 左乘A+A2得AHA+A=AH, 取共轭转置得A=A+A2, 由引理4知A为EP矩阵, 故A(A+)HA#=A(A#)HA#=(A#)H(A#)HA#=(A#)H(A+)HA+, 由推论8知A为SEP矩阵; vi)X=(A+)H时,A(A+)HA#AA+=(A#)H(A+)HA+, 即A(A+)HA+=(A#)H(A+)HA+,右乘A得A(A+)H=(A#)H(A+)H, 取共轭转置得A+AH=A+A#, 由引理9知A为SEP矩阵; vii)X=(A+)#=(AA#)HA(AA#)H时,A(AA#)HA(AA#)HA#AA+=(A#)H(AA#)HA(AA#)HA+=(A#)HAA+=(A#)H, 左乘AA+得(A#)H=AA+(A#)H, 取共轭转置得A#=A#AA+, 所以A为EP矩阵,X=(A+)#=(A#)#=A, 由(i)知A为SEP矩阵; viii)X=(A#)+=A+A3A+时,AA+A3A+A#AA+=(A#)HA+A3A+A+, 即A2A+=(A#)HA+A3A+A+, 左乘A+A得A+A3A+=A2A+, 右乘A#得A+A=AA#, 由引理4知A为EP矩阵,X=(A#)+=(A+)+=A, 由(i)得到A为SEP矩阵．

4)Y=AH时, 方程(2)转变为

AXA#AAH=(A#)HXAH,

(5)

右乘(A+)HA+, 得到方程(4),故由(3)知A为SEP矩阵．

5)Y=(A#)H时, 方程(2)转变为AXA#A(A#)H=(A#)HX(A#)H, 右乘(AH)2得方程(5), 由(4)知A为SEP矩阵．

6)Y=(A+)H时, 方程(2)转变为AXA#A(A+)H=(A#)HX(A+)H, 右乘AHA得方程(3), 由(1)知A为SEP矩阵．

7)Y=(A+)#=(AA#)HA(AA#)H时, 方程(2)转变为AXA#A(AA#)HA(AA#)H=(A#)H·X(AA#)HA(AA#)H, 右乘A+得AXA#A(AA#)H=(A#)HX(AA#)H, 再右乘AH得方程(5), 由(4)知A为SEP矩阵．

8)Y=(A#)+=A+A3A+时, 方程(2)转变为AXA#A(A+A3A+)=(A#)HX(A+A3A+),右乘A#得AXA#A=(A#)HXA+A, 再右乘AH得方程(5), 由(4)知A为SEP矩阵．