几类特殊矩阵Kronecker 积

周玉兴， 黄敬频， 刘晓冀

(1.广西师范学院 师园学院，广西 南宁530226;2.广西民族大学 理学院，广西 南宁530006)

最近几年，Krishnamoorthy S，Rajagopalan T 和Vijayakumar R 等对K-幂等矩阵做了深入研究，尤其是在K-幂等矩阵的线性组合、谱理论和广义逆理论方面取得了丰硕的成果［1-4］。然而，关于目前对k-Hermitian 矩阵的研究做得比较少［5］。文献［2］给出k-Hermitian 矩阵，k-二次Hermitian 矩阵和k-三次Hermitian 矩阵做了简单介绍，但没有深入研究。文中根据广义k-Hermitian 矩阵、k-二次Hermitian矩阵和k- 三次Hermitian 矩阵的定义，运用Kronecker 积的基本性质，研究它们和、差、积的Kronecker 积的性质，得到若干结果。

1 相关定义及引理

设Sn表示n 阶对称群，k 表示Sn中不相交对换的固定积，K 表示k 的伴随置换矩阵。K 满足K =KT== K*= K－1，且有K2= I［1-2］。定义1［1-2］设k ∈Sn，若，则矩阵A = (aij)称为k 幂等矩阵。

显然定义1 等价于KA2K = A，对此式两端分别左乘右乘K 得，KAK = A2。例如，设容易验证:KA2K = A，K2= I［1-2］。

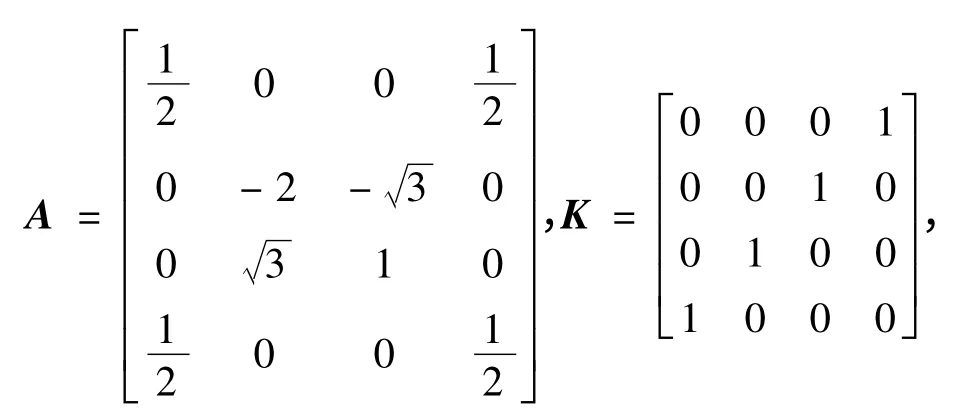
文中用到一些定义及记号［2］:若矩阵A 满足KA*K = A，则称A 为k-Hermitian 矩阵;若矩阵A 满足KA2K = A*，则称A 为k-二次Hermitian 矩阵;若矩阵A 满足KA3K = A*，则称A 为k-三次Hermitian矩阵。

定义2［6］设A = (aij)∈Cm×n，B = (bij)∈Cp×q，则称如下分块矩阵:

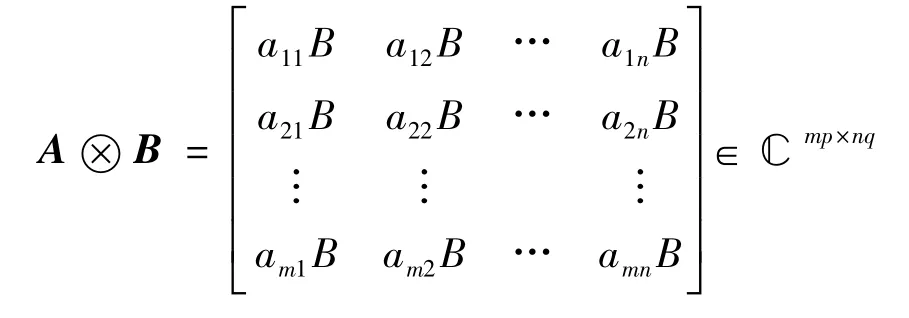
为A 与B 的Kronecker 积(或直积，张量积)。引理1［7］Kronecker 积具有如下基本性质:

1)(aA)⊗B = A ⊗(aB)，其中a ∈C，A ∈Cm×n，B ∈Cp×q;

2)(A ⊗B)*= A*⊗B*，其中A ∈Cm×n，B ∈Cp×q;

3)(A + B)⊗C = A ⊗C + B ⊗C，其中A，B ∈Cm×n，C ∈Cp×q;

4)A ⊗(B + C)= A ⊗B + A ⊗C，其中A ∈Cm×n，B，C ∈Cp×q;

5)(A ⊗B)(C ⊗D)= AC ⊗BD，其中，A ∈Cm×n，B，C ∈Cp×q，C ∈Cn×k，D ∈Cq×r。

由引理1 可知，Km⊗Kn= Knm也是伴随置换矩阵。

2 主要结果

定理1 设矩阵A，B 为k-Hermitian 矩阵

(1)A ⊗B 是k-Hermitian 矩阵;(2)若AB =BA，则(AB)⊗(AB)是k-Hermitian 矩阵;(3)(A ±B)⊗(A ± B)是k-Hermitian 矩阵。

证 1)矩阵A，B 为k-Hermitian 矩阵，KA*K = A，KB*K = B。注意到K ⊗K = K'也是伴随置换矩阵。由引理1 得A ⊗B = (KA*K)⊗(KB*K)= (K ⊗K)(A*⊗B*)(K ⊗K) = K'(A ⊗B)*K'，即K'(A ⊗B)*K' = A ⊗B。因此，A ⊗B 是k-Hermitian矩阵。

2)AB = BA，(AB)*= (BA)*。由引理1 得，AB = (KA*K)(KB*K)= KA*B*K = K(BA)*K =K(AB)*K。故AB 是k-Hermitian 矩阵。于是(AB)⊗(AB)= (K(AB)*K)⊗(K(AB)*K) = (K ⊗K)((AB)*⊗(AB)*)(K ⊗K) = K'((AB)⊗(AB))*K'。因此，(AB)⊗(AB)是k-Hermitian矩阵。

3)KA*K = A，KB*K = B，A + B = KA*K +KB*K = K(A*+B*)K = K(A +B)*K，故A +B 是k-Hermitian 矩阵。于是，(A + B)⊗(A + B)=(K(A +B)*K)⊗(K(A +B)*K)= K'((A +B)*⊗(A +B)*)K' = K'((A+B)⊗(A+B))*K'。因此，(A + B)⊗(A + B)是k-Hermitian 矩阵。同理可证，(A － B)⊗(A － B)是k-Hermitian 矩阵。

推论1 设矩阵A，B 为k-Hermitian 矩阵，存在实数λ ∈(0，1)，则(1)λA ⊗(1 －λ)B 是k-Hermitian 矩阵;(2)若AB =BA，则(λAB)⊗((1 － λ)AB)是k-Hermitian 矩阵;(3)λ(A±B)⊗(1 －λ)(A±B)是k-Hermitian 矩阵。

证 (1)由定理1 得，A ⊗B = K(A ⊗B)*K。又由引理1 得，λA ⊗(1 － λ)B = λ(1 － λ)A ⊗B =λ(1 －λ)K(A ⊗B)*K = λ(1 － λ)K(A*⊗B*)K =K(λA*⊗(1 － λ)B*)K = K(λA ⊗(1 －λ)B)*K。因此，λA ⊗(1 － λ)B 是k-Hermitian 矩阵。(2)和(3):证法同(1)。

推论2 设矩阵A，B 为k-Hermitian 矩阵，则(1)exp(A ⊗B)是k-Hermitian 矩阵函数;(2)若AB = BA，则exp((AB)⊗(AB))是k-Hermitian 矩阵函 数;(3)exp((A ± B)⊗ (A ± B))是k-Hermitian 矩阵函数。

证 (1)由定理1 得，A ⊗B = K(A ⊗B)*K。exp(A ⊗B) = exp(K(A ⊗ B)*K)。 注 意 到(K(A ⊗B)*K)k= K(A ⊗B)*K·K(A ⊗B)*K·K(A ⊗B)*K…K(A ⊗B)*K = K((A ⊗B)*)kK。((A ⊗B)*)k= ((A ⊗B)k)*。从而exp(A ⊗。于是，。故exp(A ⊗B)= K(exp(A ⊗B))*K。显然满足k-Hermitian 矩阵的定义，即KA*K = A。因此，exp(A ⊗B)是k-Hermitian 矩阵函数。(2)和(3):证法同(1)。

推论3 设矩阵A，B 为k-Hermitian 矩阵，则(1)cos(A ⊗B)是k-Hermitian 矩阵函数;(2)sin(A ⊗B)是k-Hermitian 矩阵函数;(3)arctan(A ⊗B)是k-Hermitian 矩阵函数。

证 (1)((A ⊗B)*)k= ((A ⊗B)k)*，

由定义KA*K = A 得，A ⊗B = K(A ⊗B)*K。注意到，((A ⊗B)*)k= ((A ⊗B)k)*，KK = I。从而得，(A ⊗B)2= (K(A ⊗B)*K)2= K(A ⊗B)*K·K(A⊗B)*K = K(A ⊗B)*(A ⊗B)*K = K［(A ⊗B)*］2K = K［(A ⊗B)2］*K，同理可得，(A ⊗B)4=K［(A ⊗B)4］*K，…，(A ⊗B)2n= K［(A ⊗B)2n］*K。于是cos(A ⊗B)=

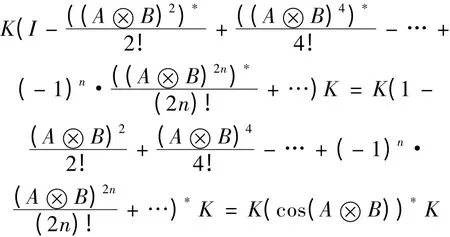
因此，cos(A ⊗B)是k-Hermitian 矩阵函数。(2)和(3):证法同(1)。

定理2 设矩阵A，B 为二次k-Hermitian 矩阵，则(1)A ⊗B 是k-二次Hermitian 矩阵;(2)若AB =BA，则(AB)⊗(AB)是k-二次Hermitian 矩阵;(3)AB +BA = 0 若，则(A ±B)⊗(A ±B)是k-二次Hermitian 矩阵。

证 1)矩阵A，B 为k-二次Hermitian 矩阵，即KA2K =A*，KB2K = B*。注意到K ⊗K = K'。由引理1 得，(A ⊗B)*= A*⊗B*= (KA2K)⊗(KB2K)=K'(A2⊗B2)K' = K'(A ⊗B)2K'。即(A ⊗B)*=K'(A ⊗B)2K'。因此，A ⊗B 是k-二次Hermitian 矩阵。

2)注意到(AB)*= (BA)*。(AB)*=B*A*=(KB2K)(KA2K)= K(AB2)K。故AB 是k-二次Hermitian 矩阵。于是，((AB)⊗(AB))*=(AB)*⊗(AB)*= (K(AB)2K)⊗(K(AB)2K)=K'((AB)2⊗(AB)2)K' = K'((AB)⊗(AB))2K'。

因此，(AB)⊗(AB)是k-二次Hermitian 矩阵。

3)注意到AB + BA = 0。∴(A + B)*= A*+B*= KA2K +KB2K = K(A2+B2)K = K(A2+AB +BA + B2)K = K(A + B)2K，即(A + B)*= K(A +B)2K。故A + B 是k-二次Hermitian 矩阵。注意到K ⊗K = K。于是，((A + B)⊗(A + B))*= (A +B)*⊗(A + B)*= (K(A + B)2K)⊗(K(A +B)2K)= K'((A + B)2⊗(A + B)2)K' = K'((A +B)⊗(A +B))2K'。因此，(A + B)⊗(A + B)是k-二次Hermitian 矩阵。同理可证，(A－B)⊗(A－B)是k-二次Hermitian 矩阵。

定理3 设矩阵A，B 为k-三次Hermitian 矩阵。(1)A ⊗B 是k-三次Hermitian 矩阵;(2)若AB =BA，则(AB)⊗(AB)是k-三次Hermitian 矩阵;(3)若AB =BA = 0，则(A ± B)⊗(A ± B)是k-三次Hermitian 矩阵。

证 (1)和(2):证明与定理2 的证法类似。以下仅证明(3):(3)KA3K = A*，KB3K = B*。注意到AB =BA = 0。A*+ B*= KA3K + KB3K = K(A3+B3)K = K(A3+ AAB + ABA + ABB + BAA + BAB +BBA + B3)K = K(A + B)3K。∴(A + B)*= A*+B*=K(A + B)3K。故A +B 是k-三次Hermitian 矩阵。于是，((A + B)⊗(A + B))*= (A + B)*⊗(A +B)*= (K(A + B)3K)⊗(K(A + B)3K)=K'((A + B)3⊗(A + B)3)K' = K'((A + B)⊗(A +B))3K'。因此，(A + B)⊗(A + B)是k-三次Hermitian 矩阵。同理可证，(A－B)⊗(A－B)是k-三次Hermitian 矩阵。

［1］Krishnamoorthy S，Rajagopalan T，Vijayakumar R.On k-idempotent matrices［J］.Int Rev Pure Appl Math，2009，5(1):97-101.

［2］Rajagopalan T.Contributions to the study on k-idempotent matrices［D］.Tiruchirappalli:Bharathidasan University，2010.

［3］Krishnamoorthy S，Rajagopalan T. Generalized inverses of k-idempotent matrices［J］. Int J Comput Appl Math，2010，5(2):227-231.

［4］Krishnamoorthy S，Rajagopalan T.Spectral and k-spectrlal theory of k-idempotent matrices［J］.Int J Math Stat，2010，7(10):81-85.

［5］Hill R D，Waters S R.On k-real and k-Hermitian matrices［J］.Lin Alg Appl，1992，169:17-29.

［6］戴华.矩阵论［M］.北京:科学出版社，2001.

［7］陈景良，陈向辉.特殊矩阵［M］.北京:清华大学出版社，2001.