“数与运算、代数初步知识、量与计量”试题精选

“数与运算、代数初步知识、量与计量”试题精选

一、填空题

1.我国2016年1月1日起实施全面二孩政策，据专家们粗略估算，二孩政策放开后，我国人口发展情况是：到2070年，出生的人口约为510000000人，横线上的数改写成用“亿”作单位的数是（ ）；死亡约9.4亿人，横线上的数读作（ ）；净减少人口约431450000人，横线上的数“四舍五入”到亿位约是（ ）。

2.低于正常水位0.56米记作－0.56米，高于正常水位1.02米记作（ ）米。

3.从0、5、6、7、8中选出3个数字组成一个能同时被2、3、5整除的最大三位数，这个三位数是（ ）。

4.用锯子锯木头，每锯一次需要3分钟。将一根木头锯成5段，一共需要（ ）分钟。

5.从3时到3时半，钟面上的分针转过了（ ）度，时针转过了（ ）度。

6．有一个数，它既是12的因数，又是12的倍数，这个数是（ ），它的因数中（ ）是质数。

7.小明家的电话号码是由8位数字组成的A5B3C3DE。其中A的最大因数是8，B有因数2和3，C是最小的质数，D既不是质数也不是合数，E既是奇数也是合数。小明家的电话号码是（ ）。

8.一个小学生，体重大约50（ ），身高大约162（ ），他每天需要饮水1500（ ），体育课上他跑100米大约用了14（ ），立定跳远跳了1.96（ ）。

9.①1个篮球场的占地面积；②1间教室的占地面积；③世纪广场的占地面积；④1个操场的占地面积。以上4个选项，占地面积最接近1公顷的地方是（ ），我是这样想的：（ ）。

10.a÷b＝7……8，b最小可以是 （ ）；当b取最小值时，a＝（ ）。

11*.对于两个数a与b，规定：a+b=a×b-(a+ b)。计算3+7=（ ）。

12.在一次植树活动中，实验小学种的树苗活了47棵，有3棵未活，这批树苗的成活率是（ ）。

13.乐乐在教室里的座位是第2列第3行，他的位置可以用数对（2，3）表示，把他往后调3排，那么他现在的位置用数对表示是（ ）。

14.小明排在一个正方形方阵队伍中，无论从方阵的哪一面看，他的位置都能用数对 （6，6）表示，这个方阵共有（ ）人。

15.爷爷今年a岁，爸爸今年（a－24）岁，5年后，他们相差（ ）岁。

16*.王强参加了一场3000米的赛跑，他以6米/秒的速度跑了一段路，又以4米/秒的速度跑完了其余的路，一共花了10分钟，王强以6米/秒的速度跑了（ ）米。

17*.在一条长100米的跑道上，小明和他的小狗分别以均匀的速度同时从跑道的起点出发。当小明走到这条跑道一半的时候，小狗已经到达跑道的终点。那么，小明与小狗的速度比是（ ）。

18*.唐僧师徒四人吃了许多馒头，唐僧和猪八戒共吃了总数的，唐僧和沙僧共吃了总数的，唐僧与孙悟空共吃了总数的，那么唐僧吃了总数的（ ）。

19*.智慧老人有一些彩色卡片，他先把卡片总数的一半又20张送给淘气，然后把剩下的一半又5张送给笑笑，最后智慧老人还剩28张卡片，智慧老人原来有卡片（ ）张。

20*.有甲、乙、丙三人同时同地出发，绕一个花圃行走，乙、丙二人同方向行走，甲与乙、丙相背而行，甲每分钟走40米，乙每分钟走38米，丙每分钟走36米，出发后，甲和乙相遇后1分钟和丙相遇，则这个花圃的周长是（ ）米。

21.一个圆形人工湖，直径200米，沿着湖边每隔4米栽一棵树，一共能栽树（ ）棵。

23.看图回答问题。

图1

（1）要围成每边有6个花片的等边三角形，需要（ ）个花片。

（2）要围成每边有7个花片的等边三角形，需要（ ）个花片。

24.小华用一样长的小棒摆出了以下三幅图（如图2），如果按这三幅图的规律继续摆下去，则第5幅图需要小棒的根数是（ ）；第n幅图需要小棒的根数是（ ）。

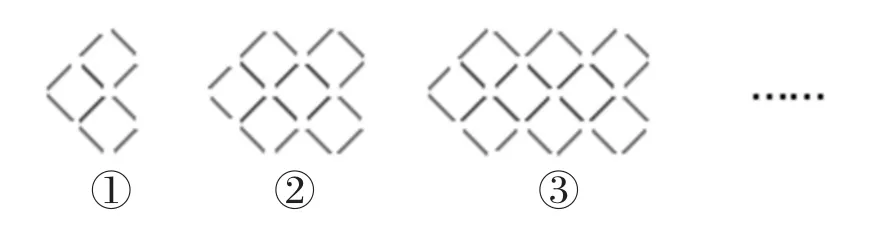
图2

25*.对一个整数进行下列操作：如果它是奇数，给它加3；如果它是偶数，把它除以2。若这个数是11，第1次操作的结果是14，第2次操作的结果是7，第3次操作的结果是10……依次操作，第2016次操作的结果是（ ）。

二、选择题

1.在下列年份中，（ ）不是闰年。

A.1900年 B.1992年

C.2000年 D.2016年

2.2016 年的2月8日，是我国农历年的大年初一，小明发现这一天正好是星期一，那么2016年的三八妇女节是（ ）。

A．星期二 B.星期三

C.星期五 D.星期天

3.在下面各数中，不需要读出零的数是（ ）。

A.23400500 B.23004050

C.23004500 D.2030045000

4.在下面4个数中，最接近0的数是（ ）。

5.下面几个数中，能满足下列所有条件的数x是（ ）。

条件：①6＜x＜22；②x是3的倍数；③x是42的因数。

A．21 B.9 C.3

6.与奇数K相邻的2个奇数是（ ）。

A.K-1和K+1 B.K-3和K+3

C.K-2和K+2 D.K-1和K+3

7.估算下面4个算式的计算结果，最大的是（ ）。

8.甲、乙两人各买了一袋同样的大米，净质量都是50千克±0.5千克，那么他俩实际所获得的大米的质量最多相差（ ）。

A.1.5千克 B.1千克

C.0.5千克 D.0千克

9.沛沛的年龄和小明相差8岁，且沛沛的年龄刚好是小明的3倍。那么沛沛的年龄是（ ）。

A.9岁 B.12岁 C.15岁

10.阿亮的钱包里有5元和10元纸币，共27张，刚好是205元。阿亮有几张5元纸币和几张10元纸币？（ ）

A．5元12张，10元15张

B.5元13张，10元14张

C.5元14张，10元13张

D.5元15张，10元12张

11．王胜与李刚两人举行100m赛跑，李刚到达终点时，王胜距离终点还有10m。如果王胜的起点不动，李刚的起点后移10m，两人的速度不变，再比一次，结果是（ ）终点。

A．王胜先到 B.李刚先到

C.两人同时到 D.不能确定谁先到

12.下列说法中，正确的是（ ）。

①两个质数的积一定是合数。

②正方形、长方形、三角形、圆都是轴对称图形。

③6克盐溶解在100克水中，盐水的含盐率是6%。

④0.9、0.99、0.999、0.9999、…，这列数的每一项越来越大，越来越接近1。

A.①和② B.②和③

C.①和③ D.①和④

13.一个两位数用a来表示，现在把1放在它的右边得到一个三位数，它的大小是（ ）。

A.100a＋1 B.10a＋1 C.a＋1

14.小明比小华大2岁，比小强小4岁。如果小华是m岁，小强是（ ）岁。

A.m-2 B.m＋2

C.m＋4 D.m＋6

16.电影票全价每张220元，优惠价每张140元，这一场电影共卖出92张票，一共收到17200元，这一场电影卖出了（ ）张优惠价的票。

A.63 B.54 C.38 D.25

17.有兄弟三人，大哥比二哥大2岁，二哥比小弟大1岁，他们三人的年龄和是46岁，下列选项中正确的一个是（ ）。

A.大哥的年龄是23岁

B.二哥的年龄是15岁

C.小弟的年龄是8岁

18.一个比的前项是2，如果前项增加6，要使比值不变，则后项应该（ ）。

A.增加6 B.增加8

C.扩大到它的3倍 D.扩大到它的4倍

19.如图3，三角形a边上的高为b，c边上的高为d。根据这些信息，下列式子中（ ）不成立。

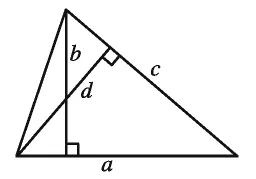
图3

20．下面相关联的量中，成正比例关系的是（ ）。

A．圆的半径与面积

B．正方形的周长与边长

C．平行四边形的面积一定，底和高

D．生产电视机的总台数一定，每天生产电视机的台数与天数

21.小明在一次数学比赛中得了86分，这次比赛一共有20道题，做对一道得5分，做错一道或不做扣2分，小明做对（ ）道。

A．19 B．18 C．17 D．16

22*.给出两列数：2、4、6、8、10、…、2004和4、9、14、19、24、…、2004，则这两列数中，相同的数的个数是（ ）。

A．201 B．202 C．402 D．404

三、判断题

1.0 既不是正数也不是负数。 （ ）

2.一个人的身份证号码中包含了丰富的信息，其最后一位表示该人的性别。 （ ）

3.如果甲数比乙数多25%，那么乙数比甲数少20%。 （ ）

5.时间经过1小时，钟面上的时针转动所形成的角是30°。 （ ）

6.一个自然数（0除外）不是质数就是合数。（）

7.来河南洛阳市参观的人数比去年增加五成，“五成”写成百分数是5%。 （ ）

8.某城市一天的最高气温为5℃，最低气温为-2℃，该城市当天的温差为3℃。 （ ）

9．小明班的全体同学1分钟跳绳的平均成绩是80下，小明跳了75下，记作“-5下”，那么小芳跳了93下，应该记作“+3下”。 （ ）

10.110 克糖放入 100克水中，含糖率为110%。 （ ）

12.两个圆半径的比是1∶3，则它们面积的比也是1∶3。 （ ）

13.一幅图的比例尺是1∶20千米。 （ ）

14.在一条线段上共有8个点，则这8个点可以构成28条线段。 （ ）

四、解答题

1.问题：哥哥的钱比弟弟的多200元，哥哥的钱是弟弟的3倍，弟弟有多少钱？

解答：用x表示弟弟的钱数，哥哥的钱数就等于3x，3x-x=200……

（1）将3x-x=200接着算下去，应该可以写出下列哪个算式？ （ ）

A.（3-1）x=200 B.（3+1）x=200

C.x=200÷3 D.x=200-3

（2）林林看完了问题，写下了另一个算式200 ÷（3-1），你觉得这个算式是否正确？（ ）

A.算式正确

B.算式错误，应该是200×（3-1）

C.算式错误，应该是200÷（3+1）

D.算式错误，应该是200-（3÷1）

2.问题：请观察图4中的规律，若要摆出10个正方形，需要几根火柴？

解答：假设n=正方形的个数。

解法一：一开始先放1根火柴，第一个正方形增加3根，以此类推，所以规律是……

解法二：第一个正方形用了4根火柴，第二个正方形增加3根火柴，以此类推，所以规律是……

图4

（1）解法一得到的规律可能是（ ）。

A.1+3n B.1n+3

C.1+4n D.4+3n

（2）解法二得到的规律可能是（ ）。

A.4n+3 B.4+3n

C.4(n-1)+3 D.4+3(n-1)

（3）两种解法都正确吗？算算看，答案是（ ）。

A.都正确，10个正方形共需要31根火柴

B.都正确，10个正方形共需要33根火柴

C.只有解法一正确，10个正方形共需要34根火柴

D.只有解法二正确，10个正方形共需要34根火柴

3.问题：请观察图5中各图形的规律，第20幅图一共有几个小正方形？

解答：图形的规律是3n+1。

当n=20时，3×20+1=

……

图5

（1）你是否同意“图形的规律是3n+1”？（ ）

A.不同意，每次只增加3个小正方形，图形的规律为3n

B.不同意，n=1时有4个小正方形，图形规律是4n

C.同意，中间固定有1个小正方形，每次增加3个

D.同意，每次只增加1个小正方形，所以要加1

（2）当n=20时，一共有（ ）个小正方形。

A.60 B.61 C.80 D.81

【注：本专号中，标“*”的题目难度稍大，可供学有余力的学生选做】