从关注思考的答案到关注答案的思考——小学生高层次数学思维能力评价方法案例研究

◇曾秀真

从关注思考的答案到关注答案的思考
——小学生高层次数学思维能力评价方法案例研究

◇曾秀真

一、问题的提出

1.为什么要测查高层次数学思维能力？

在学生学习了异分母分数加减法之后，可以设计下列题目进行巩固练习：

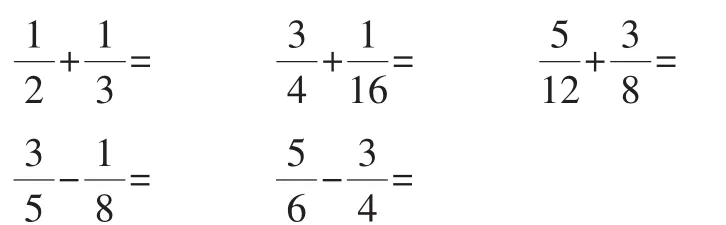
有人用这些题对某区2220名小学五年级学生进行检测，发现学生解题正确率达93%，由此得出结论，学生对异分母分数加减法的计算掌握得较好。但是，用这样的题目以这样的方式进行检测，考查的是学生对异分母分数加减法以及对通分、约分、分数化简等相关基础知识和基本技能的掌握情况，很难区分出学生数学能力水平的差异。倘若教学中不能发现那些具有高层次思维能力的学生，就不可能对他们施加有效影响，实施有差异的教学，开发学生高层次的数学思维能力也不可能真正落到实处。因此，评价学生高层次的数学思维能力，需要开辟新的途径。

2.如何命题才能评价学生的高层次思维能力？

一般来说，测试题的命制应具备三个基本条件：一是基础落实，二是思路开放，三是策略多样。以上5道异分母分数加减法测试题，如果选择其中1道题，并对命题思路进行调整，可作如下改编。

二、设计的意图

①式是异分母分数相加，联系到公倍数、通分、同分母分数加法等最基本的数学知识与技能。②式从形式上看只是①式的逆向题，但联系的知识基础与解决问题的策略与方法发生了很大的变化，不仅思路更加开放、方法更加灵活，而且所承载的数学思想方法更加多样，对学生的高层次数学思维能力构成了挑战。

1.数学方法分析。

（1）当b-a=1时，a有正整数解，且0＜a≤4；

（2）当b-a=2时，a有正整数解，且0＜a≤8；

（3）当b-a=3时，a有正整数解，且0＜a≤12；

（4）当b-a=4时，a有正整数解，且0＜a≤17；

（5）当b-a=5时，a有正整数解，且0＜a≤21；

（6）当b-a=6时，a有正整数解，且0＜a≤25；

（7）当b-a=7时，a有正整数解，且0＜a≤30；

（8）当b-a=8时，a有正整数解，且0＜a≤34；

（9）当b-a=9时，a有正整数解，且0＜a≤38；

……

结论：当b＞a，且b取大于1的任意正整数时，a有正整数解，其取值范围由b-a的差决定，b与a的差越大，a的取值范围也越大，并呈现出规律性变化，即：对于每一个b-a的差，对应的a的最大正整数解每三个又可看成一个公差是4的等差数的集合，且集合间连接数的差均为5。

2.解题思路分析。

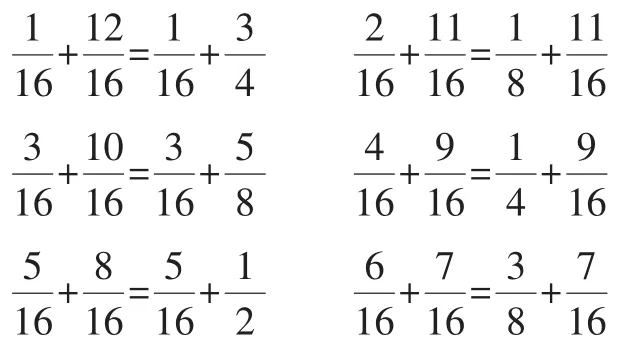
（3）根据和与加数关系逆算：减法是加法的逆运算，运用“和－一个加数＝另一个加数”，可先设定一个分数作为一个加数，再用减去设定的分数，算出另一个加数。

以上方法中，若只采用思路（1）只能得到6个算式，而采用思路（2）和（3）虽然可写很多，但会碰到计算烦琐导致出错或思路中断，均需要有序思考，对数感有较高的要求，且灵活变换解题思路，才能在短时间内写出不同算式。

三、评价标准及测试结果的分析

1.评分标准的确定分析。

为了更好地检测学生的高层次思维水平，我们在全国著名特级教师、浙江省功勋教师张天孝老师指导下，提出如下评分标准：

类别要求答案个数或解题方法种数每个答案或每种方法得分 总分基准分 4个答案 3分/个 12加分 3种方法 3分/种 9合计 21

根据解题要求“不少于4个算式”，评分时以答案达到4个算式为基准，每个算式正确得3分，基本分共12分。为了区分学生解题时不同的思维能力水平，我们对学生作业中的三项表现进行了加分：一是答案超过4个算式的加3分，二是有序思考的加3分，三是能运用扩分思路解题的加3分。以上三项加分分别对应于思维的三种品质，不同项的加分可以累加，最多共加9分。此题合计总分为21分。

2.测试结果的统计分析。

2014年6月中旬，我们在浙江省和四川省使用不同版本教材的省城学校、一般城镇学校中，随机抽取2220名五年级学生进行测试，结果显示不同区域学校的学生各分数段人数比例基本与总人数比例相接近（相关统计图略），可以看出这些样本的代表性，说明能力测试题即便是受到地区差异、教材不同等因素影响，也能检测出学生解决问题能力的差异。

全体被试的平均分是12.87，难度值是0.58，区分度是0.50。这里的难度系数接近0.6，属于较难题，且有非常好的区分度，可以作为能力测查中的优选题。应特别指出的是，平均分刚好略高于评分标准所制定的基准分12分，正好成了评判学生是否具有高层次思维能力的临界线。为了进一步说明有效性，我们对省城学校与城镇学校进行重新分类，分实验学校（即优质学校）与普通学校两大类，并从上述2220名学生中随机抽取1282名学生，对各分数段分布情况进行统计，结果如下图：

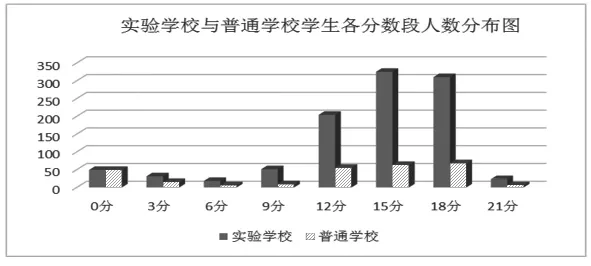
以12分作为区分低层次思维能力和高层次思维能力的临界分，上图可明显分为两部分：0～9分为低层次思维水平，其人数共占总人数的17.7%；12～21分为高层次思维水平，其人数共占总人数的82.3%。

高层次数学思维水平又可以由低到高分成不同的维度。为了进一步分析，我们对学生的创造性思考方法所得的加分进行统计，以12分为基准分，对学生解答中不同的思路与答案数，分4种不同的情况进行加分，分别称为：“加0分”“加3分”“加6分”“加9分”，四类加分情况及所占比例如下表：

水平维度百分比加0分 加3分 加6分 加9分20.2% 30.3% 29.5% 2.3%

此表表明，如果我们把高层次思维水平分成四个维度，那么四个维度的学生分布呈正态分布，这就建立了一个评价常模。

我们还将实验学校与普通学校学生的高层次思维维度分布情况进行统计分析，如下图。

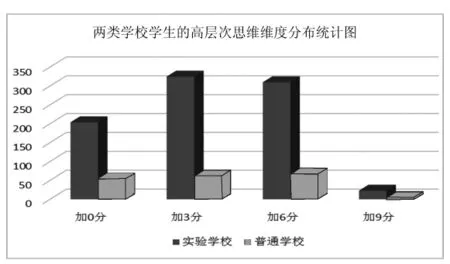
从两类学校的比较中发现，普通学校学生的高层次思维水平各维度的分布较为均衡，实验学校则表现出更大的差异性，且实验学校学生的高层次思维水平发展明显优于普通学校学生。

四、解题思路的差异性分析

我们以典型的学生作品为例，分析解题思路的差异性，着重从作品中所展现的解决问题视角来评判学生的高层次数学思维能力。

1.理解及应用（加0分）。

学生作品1：

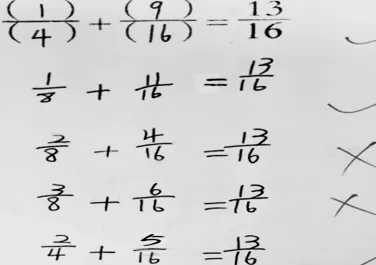
水平分析：做对3题得9分，未达基准分。错在约分后，瞬时记忆或联想出错，将约分后的数加上原约分前的数，导致不能有效运用知识解决问题。假设能够及时调整思路，则为理解及应用水平。

这一思维水平需要理解及概括开放性算式的完整意思，把所学异分母分数加减相关的通分、约分等知识技能有效应用于解题过程中，进行可逆联想。

2.推理及简化（加3分）。

学生作品2：

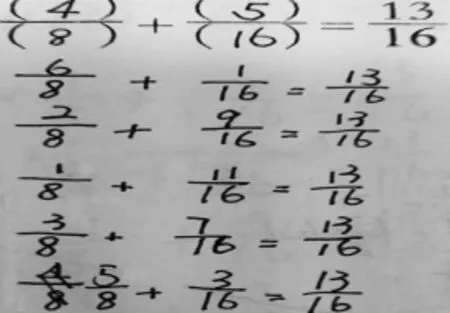
水平分析：后几式是在前几式的基础上，进行合情类推而得。这种推算有时无效，如只是对前面算式进行等值扩倍；有时有效，如对和进行重新拆分逆算；有时高效，如形成有序思考。此时规定，超过4个算式，无论几个算式，均加3分，高于这一水平的再加分。

这一思维水平要求能在解题过程中进行合情推理，迅速而广泛地将相关运算过程进行简化，再造出更多符合要求的算式来。

3.有序及灵活（加6分）。

学生作品3：

水平分析：在逆向拆分思考过程中，存在各种不同的“序”。可以按分母的因数从小到大，先拆分出分数单位来，再用和减去这个分数单位，得到另一个加数，此题正是这样思考；也可以直接将和进行有序拆分，如上图；还可以对和进行有序扩倍拆分。

这一思维水平要求在逆向拆分时，脑中随时闪现出有序思考的方法策略，同时还要灵活调整解题思路。

4.综合及创造（加9分）。

学生作品4：

水平分析：用最少算式，得到加分却最多，这是概括，是简约思维，有创意。

学生作品5：

水平分析：两种解题思路，两类解题方法，本质相同，灵活、深刻、综合。

这一思维水平要求综合运用知识，并触类旁通、创造性解题，能根据和与其中两个加数的关系在不同变化规律与方法中寻找不变的本质，达到真正的概括与简约。

以上学生作品中，对分数分解式有多种不同的表达方式，说明不同学生在解题过程中暴露了不同的差异，我们以此来关注如何思考问题的过程，分析评价小学生不同程度的数学能力发展水平。

五、反观测查后的问题及思考

我们追溯与高层次思维相关的概念，从数学思维品质的深刻性、灵活性、独创性、批判性和敏捷性等，反观本次测查与评价，尽可能从学生的思考中考察高层次思维含量。

1.思维批判性的评价。

为什么不要求所有解答有序才加3分，而只要局部有序就可以加3分？

学生作品6：

学生作品7：

过程中评价思维批判性了吗？高层次思维能力体现在过程中，而不是结果上，关键是分析学生有没有解决问题的思路，而不是关注答案的数量。超过4个算式的，不管多写几个均加3分，不以解答的个数来衡量思维水平的高低，而是进一步以有序解题加3分来衡量，这样可以分辨思维状态是处于混乱还是清晰。

我们发现，有的学生一开始就有序思考，而有的学生一开始无序解答，但能及时调整思路展开有序思考，他们边解题边总结、反思，在寻找方法和经验过程中，形成了思维的深刻性和批判性。这就表明，具有高层次思维能力的学生，在批判性方面表现出能及时纠正，能在比较中进行合情推理、分类、评估与监控，找出最佳方法或结论。

2.思维深刻性的评价。

错得越多，扣分也应越多，为什么现在出错了还比全对的得分高？

学生作品8：出错了！

分析：错了3题得满分，并加9分！错误分别是在扩分时，按分母的奇数倍扩大后造成的：扩11倍时，所拆另一分数约分后分母88错算为89；扩13倍时，分母208错写成200，26错写成25；扩17倍时，分子为13错位观察为总和的分子221。

学生作品9：全对了！

范例里追溯思维深刻性了吗？为什么出错还给满分21分？为什么全对才给18分？这不是评价出错，而是评价观念不同。学生作品9中，超过4个算式只能加3分，有序思考加3分，此外，没有其他灵活解题方法与策略就不再加分。这样的评价不以解题结果为标准，而是以思维的深刻性和灵活性为准绳。

具有高层次数学思维的小学生，在深刻性方面表现出能发现数学对象的内在联系，能主动寻找普遍意义的方法、模式，并迁移、推广到一般情境中；在灵活性方面表现出能从多个角度和多方向考虑问题，能运用多种不同方法来解决问题，并且正向思考与逆向思考互换自如，及时调整思路。

3.思维敏捷性的评价。

为什么不单独在8分钟内完成，而在学生做完前面4道题后完成？

学生作品10：

统整时考查思维敏捷性了吗？用30分钟完成以上5道题，不同学生的时间分配各不相同，如果前4题所花时间多了，则第5题只能短时间里分拆分数，知识技能越差，运用起来越缓慢。作品10表明学生知识技能已过关，为什么第4题能拆分，而第5题不能？分析原因，一是第4题分数稍简单；二是从第5题错例中得到，分子相加都等于13，但这不是同分母分数相加。说明该生正向思维与逆向思维统配时失调，只需稍作引导即可，或者说只要单独给足8分钟，突破0分很有希望。由此，这种以题组系列进行的评价，有利于考查思维的敏捷性，使学生在思维敏捷性方面表现出能很快理解题意并判别题目模式，自觉运用方法，缩短解题时间。

对于学生来说，在解决非常规问题的过程中，当一种方法无法满足时，需要变序思考其他解题策略，这时综合应用能力和思维的创造性便显露出来，说明这样的评价具有考查学生创造性思维能力的功效。具有高层次思维能力的学生，在创造性方面表现出能从“新视角”观察与分析，不受常规限制，能产生创造性想法。

（作者单位：浙江温州市鹿城区教师培训和科研中心）