“图形与几何”总复习教学建议
2017-06-15陈晓燕
◇陈晓燕
“图形与几何”总复习教学建议
◇陈晓燕
一、整体构建“图形与几何”领域知识网
复习的目的之一是帮助学生构建知识网,强调的是“构建网络、形成系统”。在总复习阶段,每个领域的第一课时应用于整个领域知识网的建构。就“图形与几何”而言,总复习的第一课时需要帮助学生建构以下知识网络(如图1)。

图1
在教学中需要关注以下几点:
(一)整个内容领域知识网的建构不宜过细,关键是梳理核心知识和基本概念,以形成系统,建立整体认知。
(二)在整体建构基础上,后续每节课的复习可根据需要截取其中一部分进行细化。
(三)呈现的方式可以多样,图1只是其中一种。
(四)整体建构可以安排在每个领域总复习的第一课时,也可安排在最后一课时,即采用 “总—分”或“分—总”的方式。
二、有效运用现代技术,准确把握复习重点
“查漏补缺”是复习教学另一重要目的。只有明晰学生的“漏”和“缺”在哪儿,才能有针对性地设计复习内容,从而提高复习效果。那么,如何查“漏”和补“缺”呢?典型错例的收集、不同题目的分类等,可以有效地帮助学生的学和教师的教。在“互联网+”的时代,技术手段能更精准地把握学生的“漏”和“缺”。在复习教学中,可以利用问卷星、微信等工具或教育服务平台中的专用软件,提前发布复习题,对学生完成情况做详细的统计,基于数据准确把握学生对所学内容的掌握情况。在此基础上,依学情设计复习内容,确定复习程序,选择复习策略。
如,有教师在复习“长方体和正方体的表面积和体积”这一内容时,课前设计了以下“检测单”,用于检测学生学情。
1.一个长方体长9cm,宽4cm,高5cm,计算它的表面积的正确算式是( )。
A.(9+4+5)×4 B.(9×4+9×5+4×5)×6
C.9×4×5 D.(9×4+9×5+4×5)×2
2.一个正方体的棱长是 4dm,它的体积是( )dm3。
A.16 B.48 C.64 D.96
3.给一个棱长2dm的正方体包装盒的四周都贴上商标,贴商标的面积是( )dm2。
A.8 B.16 C.20 D.24
4.下面( )问题与体积有关。
A.包装一份生日礼物需要多少彩纸
B.一个玻璃球沉入装满水的杯子中,溢出多少水
C.油漆大厅里的柱子,需要多少油漆
D.给一个玻璃柜台各边装上角铁,需要多少角铁
5.把棱长为2cm的三个正方体木块拼成一个长方体,这个长方体的表面积是( )。
A.24 B.72 C.28 D.56
通过统计每题的正确率,发现学生做第1~3题的正确率均在90%以上,第4题为81%,第5题为63%。同时,对出错的题逐一进行统计和归因分析,并对学生进行访谈,基于数据,制定了课堂复习的侧重点,确定了针对每个复习重点提问和个性化辅导的学生名单,并对第5题做了题组设计。这样的复习,有的放矢,针对性更强,效果更好!
三、注重基础,发展空间想象力
(一)落实基础,突出核心知识。
总复习阶段,不少老师容易出现以下两种倾向:一是搜集各类习题,恨不能把所有好题全给学生做一遍;二是忽视基础,偏向于让学生完成更多综合性强、思维难度大的习题。殊不知,如果学生没有巩固核心概念、掌握基础知识,一味做题,只会事倍功半。就“图形与几何”领域的总复习而言,如何做到既落实基础,又适当综合提升呢?
1.先梳理,再练习。
梳理不仅仅可以构建知识网,形成系统,还可以帮助学生唤醒记忆,巩固所学,对基本概念、核心知识进一步熟悉和掌握。
2.基础性习题不可少。
对于学生而言,总复习是学习“补救”和“提升”的机会。复习相当于“新知”学习,不仅帮助学生重新温习基本概念,更为重要的是梳理基本概念之间的联系与区别,以便于更好地适应不同层次学生的复习需求。
3.运用题组,兼顾基础和综合。
例1:如图2,一个圆柱体容器(不计厚度),底面半径为5厘米,高20厘米,里面水深15厘米。
(1)如果全部装满水,能装多少毫升?
(2)容器与水接触部分的面积是多少平方厘米?

图2
此题组中的第(1)小题为基础题,考查学生对容积的理解及圆柱体积公式的基本运用;第(2)小题则适当综合与提升,要求学生具备阅读理解,选择有用信息,计算圆柱侧面积和底面积等相关能力和知识基础。
例2:根据图3中的信息解答下面各题。
(1)这个直角梯形的面积是多少平方厘米?
(2)如果以AB边为轴旋转一周,得到一个立体图形,这个立体图形的体积是多少立方厘米?

图3
此题组中第(1)小题是梯形面积公式的直接运用,是基础题;第(2)小题则涉及空间想象、圆柱和圆锥体积的计算,难度和综合性都比较强。
(二)关注核心素养,发展空间想象力。
“图形与几何”领域的教学,空间观念的培养是核心目标,而空间观念的核心要素就是空间想象力。
小学阶段,学生空间想象力主要体现在以下几方面:
1.二维与三维的转化。
(1)平面到立体。主要有两种类型:
一是展开图与立体图的对应关系,有以下两个层次。
①给出一个展开图,判断是否能折成相应立体图形。
例3:下面的展开图能围成长方体或正方体的是( )。

②展开图与立体图各要素(面、线等)的对应。
例4:图4中,左图是右图的展开图,“?”表示的是( )。
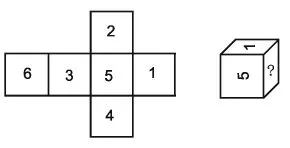
图4
二是判断平面图形以一边为轴旋转360°所形成的立体图形(如图5)。
例5:连线。
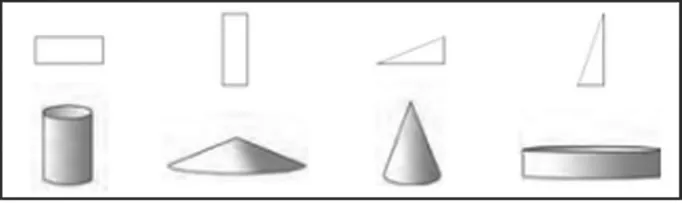
图5
(2)立体到平面。主要包括:求长(正)方体、圆柱的表面积;求长(正)方体某个(或几个)面的面积;求立体图形截面面积等。其中,求某个(或几个)面的面积对学生的空间想象能力要求最高,因为求所有面的面积时,学生通过套用公式即可求得结果,但是求某个(或几个)面的面积,则需要建立准确的对应关系。如下题,不仅需要学生明晰要求的是哪几个面的面积,还要将每个面的长和宽与长方体的长、宽、高相关数据建立对应关系,才能准确列式计算。如果没有图6,只有文字描述,则对学生的空间想象能力要求更高。
例6:一个长方体饼干盒,长17厘米,宽11厘米,高22厘米。如果在它的侧面贴满一圈包装纸(如图6),包装纸的面积至少有多少平方厘米?

图6
2.图形的运动。主要是图形的平移、旋转、轴对称。
例7:一个直角梯形,上底4厘米,下底8厘米,高5厘米,如果以它的一条直角边为轴旋转一周,将形成一个立体图形,求这个立体图形的体积。
分析:此题具有开放性,以不同的直角边为轴旋转后所形成的立体图形不一样。学生不仅要根据描述的语言在头脑中想象出直角梯形,还要在头脑中想象旋转后形成的立体图形的直观图,并准确建立各部分对应关系和数量关系,才能准确解答。
例8:请你制作一个无盖圆柱形水桶,有图7中几种型号的铁皮可供搭配选择。
(1)你选择的材料是( )号和( )号。
(2)用你选择的材料制作的水桶,容积是多少?

图7
分析:此题同样是一道开放题,答案开放,且有干扰信息,需要学生将圆柱与其展开图以及展开图各部分(侧面与底面)的形状、位置关系、数量关系一一对应,对学生空间想象力要求较高。
(作者单位:广东东莞市教育局教研室)
