从问题中来,到问题中去
——小学数学“式与方程、比和比例”的复习建议
2017-06-15吴兴元顾跃超
◇吴兴元 顾跃超
从问题中来,到问题中去
——小学数学“式与方程、比和比例”的复习建议
◇吴兴元 顾跃超

“式与方程”和“比和比例”是小学数学“数与代数”领域的重要内容,复习时需要关注学生的概念理解、运算能力和解决问题三个层面的目标。如何引导学生在问题中进行整理复习、巩固应用、发展能力和提升素养,实现复习教学求知、求联、求发展的总体目标呢?
一 借助问题经历知识梳理,深化概念理解
1.关于“式与方程”。
小学数学教学对代数式——含有字母的式子的基本要求,是借助现实情境和简单问题中的数量关系分析,理解用字母表示数的意义,知道代数式既可以表示一个数量,也可以表示一种数量关系。如小明今年 a岁,爸爸比小明大28岁,那么(a+28)岁既表示爸爸的年龄,也表示爸爸年龄和小明年龄的数量关系,学生容易产生混淆。在复习时,我们可以设计一些问题情境帮助学生进一步理解。
如,已知体育用品店里,每个足球售价a元,每个排球售价b元。
(1)买3个足球和2个排球要( )元。
(2)式子“4b-a”表示的意思是( )和( )相差的钱。
(3)根据已知信息,请你写出一个含有字母的式子:( ),这个式子所表示的意思是( )。
第(1)题考查学生是否能够根据问题情境写出代数式。第(2)题是逆向的,考查学生是否能够根据代数式理解其含义并表述问题。第(3)题则是考查学生是否能够根据信息独立提出问题并用代数式进行表达。需要说明的是,小学不要求学生认识代数式的严格定义,在实际问题中理解代数式即可。
而对于方程,教材一般会给出描述性定义——像100+x=250、3x=2.4……这样,含有未知数的等式就是方程。方程的本质是描述与刻画现实世界的数量关系和空间形式的数学模型,小学不要求学生机械记忆方程概念,其基本要求是能用方程表示简单情境中的等量关系,了解方程的作用。因此,在复习时应当侧重在实际问题中帮助学生进一步理解,可设计如下的问题。
(1)根据图意,列出方程。
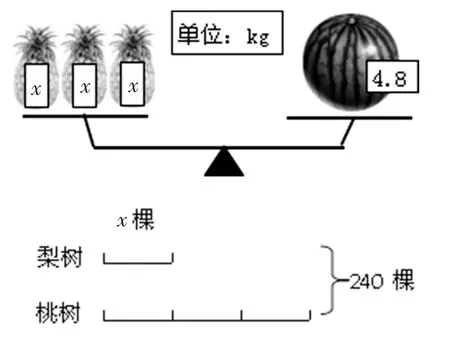
(2)根据下面哪句话的信息可以列出方程6x+5=37?
A.一副羽毛球拍售价37元,比6根短绳的价钱贵5元。
(2)根据下面哪句话的信息可以列出方程6x+5=37?
A.一副羽毛球拍售价37元,比6根短绳的价钱贵5元。
B.一副羽毛球拍售价37元,比6根短绳的价钱便宜5元。
(3)请你写出一个能用方程“6x+5=37”解决的问题。
第(1)题是基本练习,重点考查学生能否读懂题意,找到等量关系,列出方程。第(2)题侧重考查学生能否分析发现数量关系的区别,判断方程和问题的匹配性。第(3)题则是考查学生能否根据方程写出问题情境,有一定的挑战性。通过这样的复习,来检查学生是否从本质上理解方程。
2.关于“比和比例”。
“比和比例”这两个数学概念是紧密联系的,具体包括比的定义、比值、最简比、比例的定义、解比例、比例尺、正比例和反比例等。复习时部分概念可以整体推进,个别概念则需要专项练习。
如可以设计以下的问题:
(1)观察下图,你能写出哪些比?哪些比例?

(2)根据下面图形中的数据,你能写出哪些比例?还有什么发现?
单位:厘米
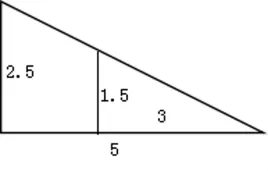
第(1)题主要考查学生能否根据情境和数据找到尽可能多的比和比例。首先从比的情况看,可以写出小树和大树高度的比、影长的比,小树和大树各自影长和高度的比等。进而引导学生发现,哪些比可以组成比例?既可以从比值来判断,也可以从比的意义来判断。第(2)题是从三角形的线段长度比展开的,学生既可以写出各种不同比值的比,也可以发现多个比例:1.5∶3=2.5∶5和3∶5=1.5∶2.5,把这两个比例的内外项进行交换,又可以组成两个新的比例。
关于正比例和反比例的复习,需要设计专项练习,仍可通过问题形式呈现。如可以设计如下问题:
(1)观察。表中的两个量成比例吗?如果成,成什么比例?
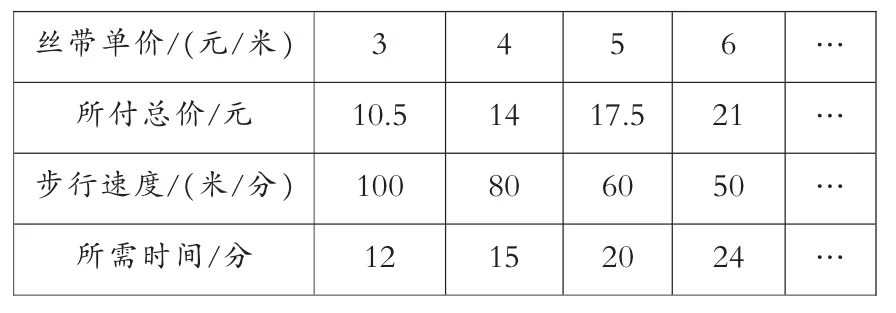
丝带单价/(元/米)3 4 5 6 …所付总价/元 10.5 14 17.5 21 …步行速度/(米/分)100 80 60 50 …所需时间/分 12 15 20 24 …
(2)判断。下面每组中的两个量成比例吗?如果成,成什么比例?
①六(3)班有42个学生,班里的男生人数和女生人数。
②六(3)班有42个学生,平均分成若干组,每组人数和分的组数。
③圆锥体积一定,圆锥的底面积和高。
④圆锥高一定,圆锥的底面积和体积。
第(1)题是一组基本练习,重点考查学生能否通过分析数据,从正、反比例的基本定义出发,进行判断。第(2)题相对要复杂一些,主要考查学生能否通过多种方法自己进行判断,可以用数据举例说明,也可以根据两个量之间的数量关系来思考。此外,我们还可以借助图的形式来设计正、反比例的判断练习。
二 借助问题巩固计算技能,提升运算能力
“式与方程”和“比和比例”也都涉及运算。解方程、求比值和解比例是小学数学教学中重要的运算技能,为了凸显运算的作用及更好地进行检验,建议借助具体问题进行复习教学。
1.关于解方程(比例)。
从结构形式看,解方程也包含了解比例,都是根据已知数据和等式求未知数的过程。两者都可以根据等式性质说明每一步的计算过程,也可以根据运算符号和数据特点选择灵活合理的简便方法。其中检验结果是否正确,也是特别需要培养的计算习惯之一。
(1)鞋的尺码通常用“码”或者“厘米”作单位,它们之间的换算关系是:b=2a-10。(b表示码数,a表示厘米数)
①小明穿的鞋子是23厘米,也就是( )码。
②王老师穿的鞋子是42码,也就是( )厘米。
(2)一个足球是用12块黑皮和20块白皮缝制而成的,王师傅在缝制过程中一共用掉了60块白皮,那么相应地用掉了多少块黑皮?解决这个问题时,小红是这样写的:设用掉了x块黑皮。12∶x=20∶60。正确结果是( )。
A.24 B.36 C.48 D.60
(3)解下面的方程或比例。

2.关于求比值和化简比。
“求比值”和“化简比”是学生比较容易混淆的内容,复习时要帮助学生明白:比值表示的是前项和后项相除的结果,是一个数;化简比则表示不管用什么方法,最后仍旧是一个比,还是表示两个数量的关系。实践证明,在实际问题中进行复习更合适。
(1)张师傅28天完成了1260个零件的加工任务。
①零件总数和加工天数的比是( ),化简后是( )。
②零件总数和加工天数的比值是( ),这个比值表示( )。
(2)化简下面的比。

三 借助问题培养发现和提出、分析和解决问题能力
1.侧重数量关系分析解决问题。
小学数学中的数量关系有两个基本模型:一个是求和模型,即部分+部分=和;另一个是求积模型,如单价×数量=总价、速度×时间=路程。用方程(比例)解决问题的数量关系还是一样的,只是在分析问题上和原来的算术思维不同,将未知量假设为已知的,参与到等量关系的建立和具体运算中,这都是设计问题时需要考虑的。
(2)一个容器里装有盐水,盐和水的比是1∶25,再往这个容器里放入6克盐和10克水,盐和水的比达到了1∶11。原来容器里装有多少盐水?
(3)幼儿园老师给大(1)班小朋友分糖。如果每人分2颗,则多7颗,如果给每人分3颗,就缺18颗。大(1)班有多少位小朋友?一共有多少颗糖?
这三道复习题难度有所不同,考查目的也各有侧重。第(1)题的数量关系比较常见,一是分数问题关系,“增加边长的”表示新正方形边长=原来正方形边长×;二是边长和周长的关系,即正方形边长×4=周长。学生只要能找到等量关系就行。
第(2)题略有变化,在解读信息和分析关系时,需要知道盐水前后的变化,得到(原来盐的质量+6克)∶(原来水的质量+10克)=1∶11;列方程时,还需要思考先设哪个未知量为x,由此可以清楚了解学生是否真正掌握了列方程解决问题。
第(3)题的情境是学生很少接触的,如果用算术解法学生比较难解释,用方程解法可以体现其优越性。如设小朋友有x人,那么糖有(2x+7)颗或者(3x-18)颗。可以列出方程 2x+7=3x-18。复习时,需要强调通过分析获得等量关系是解决问题的关键。
2.侧重发现和提出数学问题。
解决他人提出的问题固然重要,但是能够发现新的问题、提出有价值的问题更重要,这是对创新性人才的基本要求。如何在复习教学中落实这一目标呢?这需要教师的创新设计。
(1)用一个长方形A在下图中任意框出4个数。

①你想到了什么问题?
②如果用a表示这4个数的左起第一个,其他3个可以怎么表示?
③按照这样的框法,如果知道这4个数的和是210,那么这4个数分别是多少?
(2)根据前面的学习,你能否提出一个新的数学问题?
第(1)题的主要目的有两个:一是给予学生提出问题的机会;二是解决后面两个小题时,需要用到代数式和方程(也可以用算术方法思考),融会贯通两种不同的思路。第(2)题考查学生的举一反三能力、发散求异思维能力。如果学生能提出如下的问题:用长方形B框出的4个数有什么特点?如果第一个数用a表示,其他3个数可以怎么表示?……如果学生能够创新性地提出用不同的图形来框出4个(如长方形C)、5个或者6个数,研究其规律,用代数式来表示,用方程来解答,那就更有意义了。
3.侧重综合运用知识解决现实问题。
小学数学教学应当承担起培养学生的应用意识,使学生认识到现实生活中有大量的问题可以抽象成数学问题,利用数学概念、原理和方法能解释现实世界中的现象,解决现实世界中的问题。这在“比例尺”的复习教学中,体现得最为明显。
(1)学校需要在校门口的橱窗里贴出校园平面图。要画出这张平面图,需要考虑哪些问题?请你设计一个方案。
(2)请以四人小组为单位,完成这张校园平面图的设计任务。
要解决这个问题,学生需要走出教室,实际去做。问题(1)很有挑战性,需要学生思考完成任务的步骤,用到哪些工具,要综合运用方位、平面图形、比例尺等知识解决问题。问题(2)依靠个人的力量很难完成,需要小组合作。这是一项数学综合实践活动。在复习阶段,根据内容适当安排解决这样的问题很有价值,可以使学生体会数学与生产、生活的紧密联系。
(作者单位:浙江海宁市教师进修学校,海宁市袁花镇中心小学)
