突然开孔结构风致瞬态内压极值研究

余先锋， 段 旻， 谢壮宁

(1.华南理工大学 亚热带建筑科学国家重点实验室,广州 510640; 2.重庆大学 城市科技学院 土木工程学院,重庆 402167)

突然开孔结构风致瞬态内压极值研究

余先锋1， 段 旻2， 谢壮宁1

(1.华南理工大学 亚热带建筑科学国家重点实验室,广州 510640; 2.重庆大学 城市科技学院 土木工程学院,重庆 402167)

基于经典内压控制方程，对特定开孔时刻下的瞬态内压峰值响应进行了详细研究，分析孔口开启时间对结构瞬态内压峰值的影响。提出突然开孔结构瞬态内压极值的估算方法，并与精确算法进行对比。结果表明：门窗开启时刻的外压值越大，瞬态内压峰值越大，但两者最大值之间存在着一定的时差；瞬态内压极值与外压达极值时的瞬态内压峰值之间的比值可用放大因子G=1.17来描述；提出的极值计算方法能有效地估算突然开孔结构瞬态内压极值。

过冲效应；瞬态内压；时差；放大因子；风洞试验

结构在强风中由于门窗突然受损，内压瞬间增大，极易导致围护结构破坏。灾后调查表明[1]，屋面上任一处的砖块在台风时都有可能被风吹起，形成容重很大的飞掷物，极易导致建筑物迎风面门窗破坏而突然出现大开孔，若此时门窗处的外压达到极值时内压过冲现象将极为剧烈。而目前对风致内压的研究大多集中于开孔后的稳态内压上，风工程学者在考虑屋盖柔度、背景孔隙、内部分区等因素后不断完善了内压控制方程[2-4]，并开展了大量的风洞试验研究[5-7]。

在突然开孔结构瞬态内压研究方面，Stathopoulos等[8]采用膜的快速溶化技术和照相机快门技术模拟建筑结构迎风墙面的突然开孔，并将风洞试验结果与理论计算结果进行了对比，研究表明当结构出现突然开孔时，内压瞬态过冲响应小于随后的稳态内压峰值。然而，段旻等[9]通过“电磁阀-强力弹簧”系统来控制门窗的突然开启，在确保模型气密性的条件下成功进行了突然开孔结构瞬态内压风洞试验，试验结果与理论分析均表明，当开孔时刻的外压取极大值时，瞬态峰值内压明显高于后续的稳态结果。

虽然由风洞试验捕捉到了瞬态内压过冲现象，但突然开孔采用的是被动方式，无法确保当外压达到极大值时门窗突然开启。而目前单空间结构风致内压控制理论较为成熟，其内压控制方程也经过了众多风洞试验的验证，因此从理论上研究突然开孔结构瞬态内压的极值有着重要的意义。

文中基于经典的内压控制方程，通过合理边界条件与外压激励时程的设定，对特定开孔时刻下的内压瞬态峰值响应进行了研究，考察了门窗开启时间对内压峰值的影响，最后给出了多样本下瞬态内压极值的估算方法。

1 内压过冲现象的试验验证

1.1 风洞试验概况

内压试验模型采用刚性材料制作而成，如图1所示，模型尺寸为19 cm×30 cm×50 cm(高×宽×长)，孔口高度为11 cm，按缩尺比为1∶30模拟高5.7 m的典型低矮建筑。开孔率(定义为开孔面积与内部容积的2/3次幂之比)为5%～20%，开孔方式为由直流电磁阀控制的被动开启方式，各工况均只考虑来流正吹的最不利风向角。

图1 风洞试验模型

风洞试验是在一试验段尺寸为3 m×2 m×20 m(宽×高×长)的大气边界层风洞中进行的，大气边界层流场按GB 50009—2001模拟了B类地貌风场，内压测点布置及模拟的平均风速、湍流度剖面及屋盖高度处的脉动风速谱见文献[9]。试验中采用Scanivalve公司的DSM3200系统进行瞬态内压测量，采样频率为1 250 Hz，每个测点的样本长度为20 480。

1.2 试验结果分析

图3为瞬态和稳态内压系数峰值随开孔率的变化，从图中可以看出，瞬态内压峰值随开孔率的增加而增加，而稳态内压峰值随开孔率的变化相对较小；瞬态峰值内压系数明显大于相应稳态峰值内压系数；试验观察到的最小过冲比(过冲比定义为瞬态内压峰值与稳态内压极值之比)为1.17，这说明仅考虑稳态内压极值来进行结构抗风设计将会偏于危险。

(a) 5%开孔率的瞬态内压系数时程

(b) 20%开孔率的瞬态内压系数时程

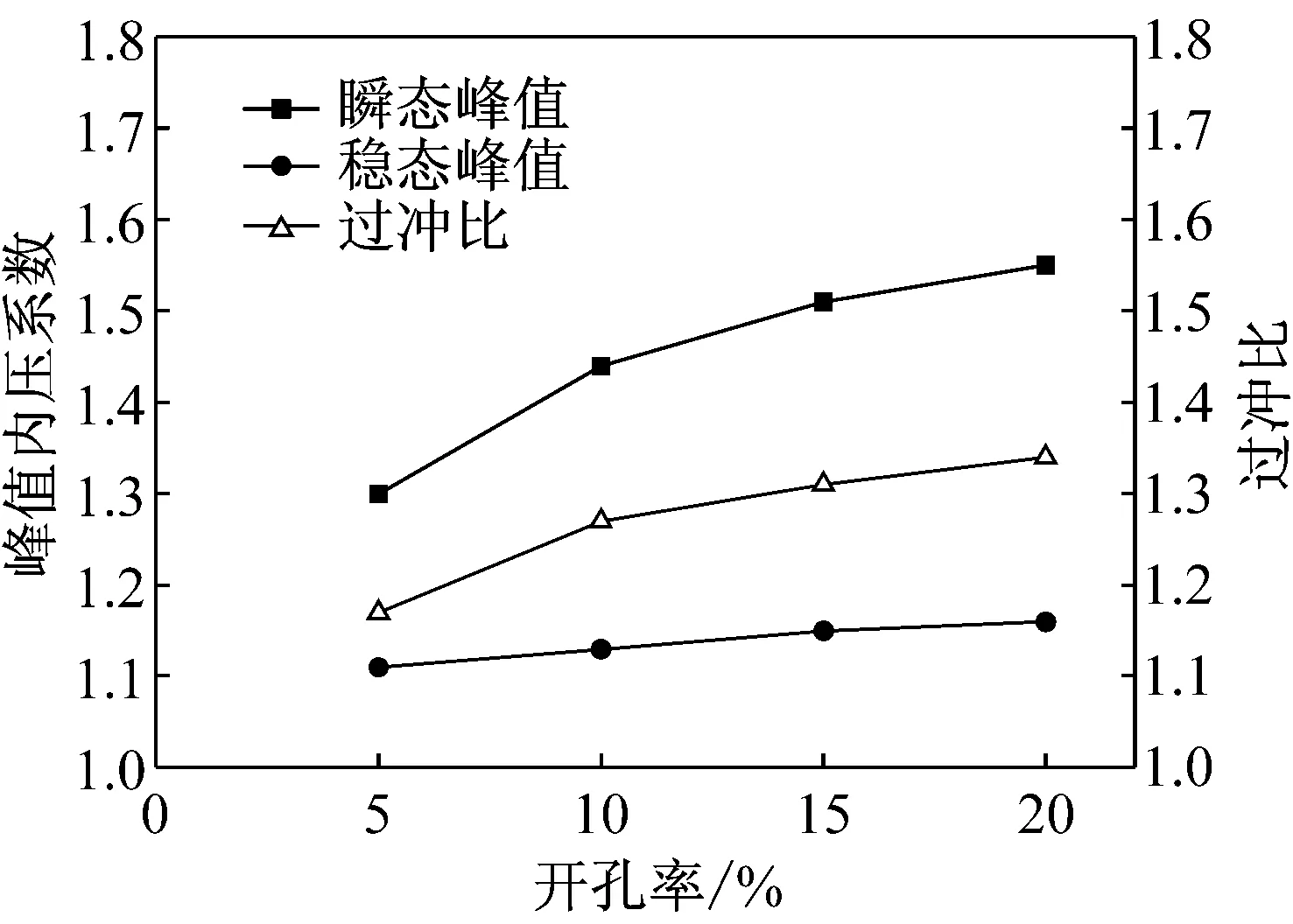
图3 各种开孔率下的峰值内压系数及过冲比

Fig.3 Peak internal pressure coefficients and overshooting ratios in different opening ratios

2 内压控制理论与计算模型

虽然通过风洞试验捕捉到了瞬态内压过冲现象，但由于开孔方式是被动的，无法确保当外压达到极大值时门窗突然开启，而内压控制方程经过了众多风洞试验的验证，因此借助内压控制方程从理论上研究突然开孔结构瞬态内压的极值是可行的。

2.1 内压控制方程与初始条件

对于单开孔结构，Vickery等[10]提出了内压控制方程，如式(1)所示

(1)

当结构带有背景孔隙时，参考文献[3]导出了相应的内压控制方程，见式(2)

(2)

2.2 外压激励模拟

孔口处的外压激励由模拟方法获得，根据Shinozuka等[11]的理论，风速随机过程v(t)可通过式(3)进行模拟

(3)

式中:S(ω)为目标风速谱；Δω为频率步长；φn为(0,2π)之间均匀分布的随机相位。

文中采用的目标风速谱为Karman谱如式(4)所示

(4)

根据试验段风场特性，将湍流度I取为0.2，Lu(z)取为20 m；模拟频率段范围为0.008～8 Hz，模拟频率步长为0.008 Hz。开孔处风速时程与功率谱模拟结果见图4与图5，由图4～图5可知，模拟的风速谱与目标谱吻合得很好；风速时程中的各项统计结果也与理论值一致。

2.3 计算模型

计算模型如图6所示，孔口中心计算高度为3.4 m，开孔率与背景孔隙率(定义为背景孔隙总面积与内部容积的2/3次幂之比)计算范围分别为1%～25%与0.02%～0.4%。风压系数的参考高度统一取为10 m。

图4 模拟的开孔处风速时程

图5 模拟的开孔处风速谱

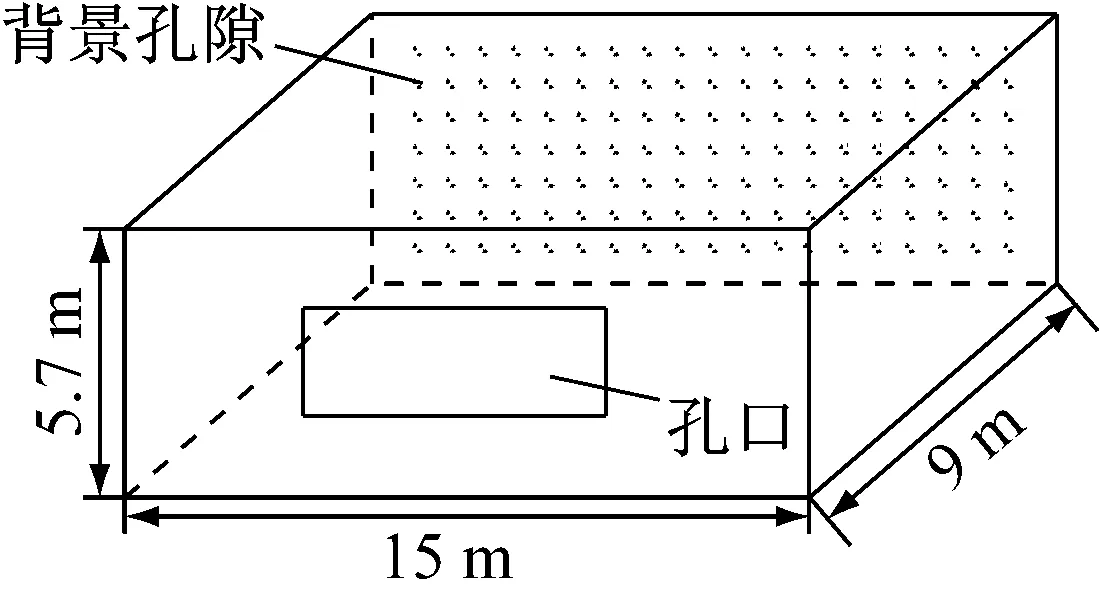
图6 计算模型图

3 开启时间对瞬态内压峰值的影响

以0.01 s作为开启时间间隔，计算得到的风压系数时程随开孔时间的变化如图7所示。由图7可知：①开孔时刻的外压水平是瞬态内压峰值的决定性因素(当开孔瞬间外压较大，则过冲现象明显)；②瞬态内压峰值与相应开孔瞬间的外压变化规律是相同的，但两者最大值(最大的瞬态内压峰值为2.16，而相应的开孔瞬间外压峰值为1.93)并没有同时出现，而是存在着一个极短的时间差(简称时差，瞬态内压峰值发生时间提前约为0.1 s)。

图7 不同开启时间瞬态内压峰值

Fig.7 Peak value of the transient internal pressure at different opening time

4 瞬态内压极值估计

4.1 基本思想与步骤

由于模拟的风速具有随机性，须采用多样本统计平均法来估算瞬态内压极值。由第“3”节分析可知，当开孔处外压达极大值时瞬态内压峰值并非最大值，两者之间存在一定的时差，但时差无法精确确定，意味着每次计算时均需试算多种开孔时刻，这极其繁琐且计算量巨大。

为此，提出简化的瞬态内压极值估算方法，计算步骤如下：

(1) 模拟出N条外压样本时程，并分别找出各样本中最大值所在的时刻作为开孔时刻；

(2) 在外压达最大值时开孔，求出N个外压样本下的N个瞬态内压峰值，形成内压峰值样本；

(3) 对N个样本的内压峰值集合，利用分段峰值平均法[12]进行极值估算，从而得到瞬态内压峰值样本的极值(当孔口外压达最大值时)；

(4) 对求出的内压极值进行时差放大处理，即乘以放大因子G(G定义为瞬态内压极大值与孔口外压达极值时的瞬态内压峰值的比值)，于是可得真实的瞬态内压极大值。

4.2 放大因子G

为取得合理有效的放大因子G，模拟了N=200条外压激励样本，样本长度均为600 s，在外压达最大值的前τ=0.5 s内以时间间隔Δt=0.01 s进行50次瞬态内压峰值计算，从而确定各个样本下的真实瞬态内压极大值所在时刻与大小。

对于开孔率为10%的结构，瞬态内压极大值与瞬态内压峰值的对比见图8，注意瞬态内压峰值是将开孔时间定为外压取极大值时得到的，图8中亦给出了放大因子G的拟合公式。由图8可知，各样本下瞬态内压极大值均较瞬态内压峰值大；放大因子G的拟合效果良好，相关系数高达0.988 5。

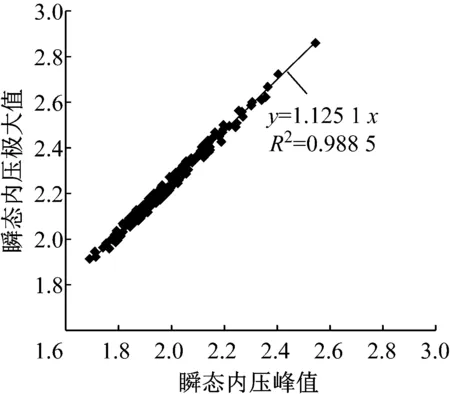
图8 瞬态内压峰值计算结果

图9为不同开孔率与背景孔隙率下放大因子G的拟合结果，其中带背景孔隙结构的开孔率为25%，由图中可知：放大因子G随着开孔率的增大而增大，随背景孔隙率的增大而减小，但两者对G(变化范围仅为1.11～1.16)的影响不大。

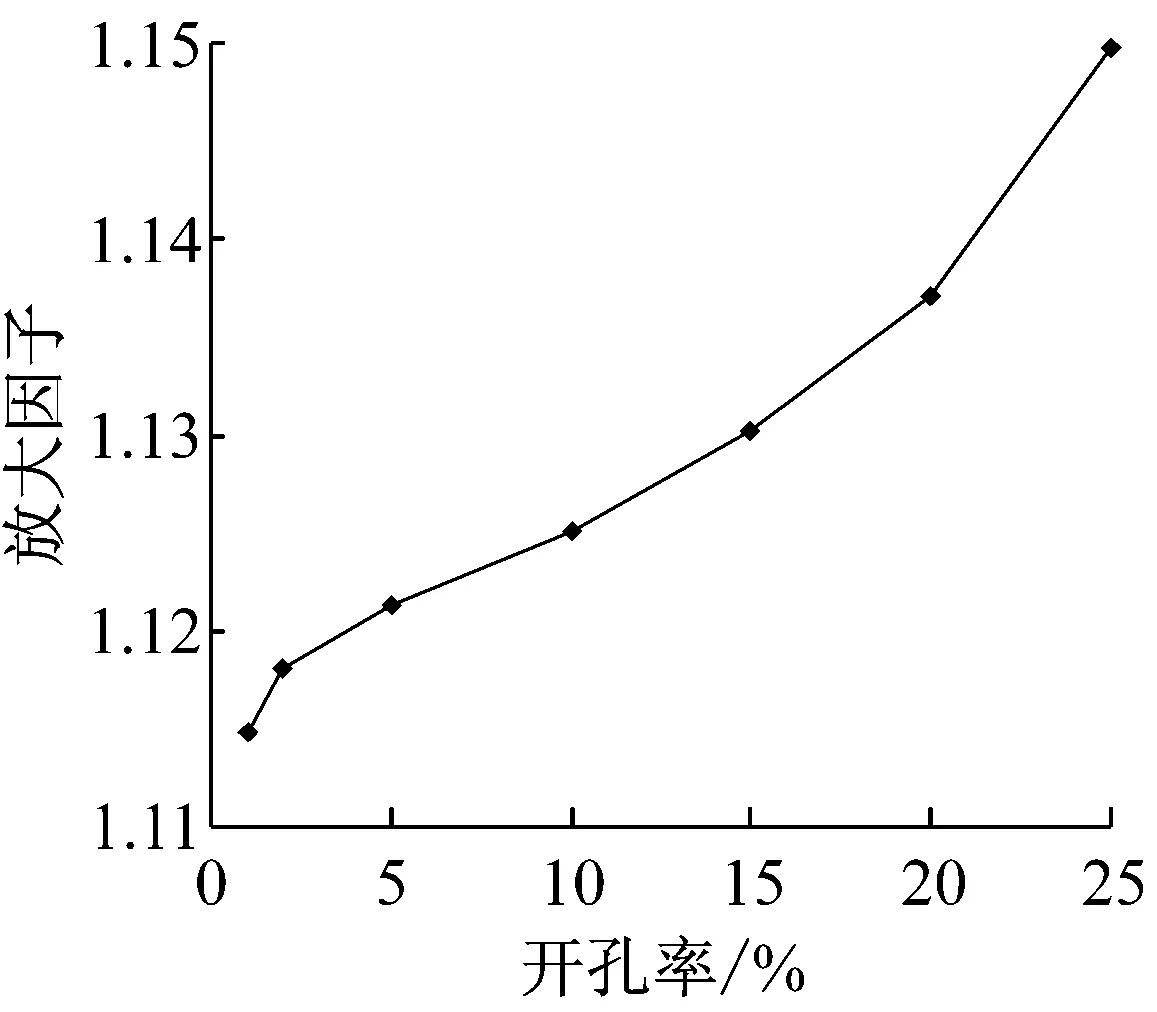
(a) 开孔率

(b) 背景孔隙率

表1为不同孔口损失系数(2.68～40)、内部容积(100～10 000 m3)与湍流度(0.10～0.30)下放大因子G的拟合结果，各因素的取值范围涵盖了绝大多数实际工程。由表1可知：①放大因子G随着损失系数与内部容积的增大而减小，随着湍流度的增大而增大；②各工况下拟合的相关系数均接近于1，拟合效果良好。值得注意的是，放大因子G的变化范围均不大，所有工况下均保持在1.11～1.17。因此，在实际工程中，取一个统一的放大因子1.17来简化计算是完全可行的。

4.3 计算结果分析

据“4.2”节中的结论，文中对放大因子统一取为1.17。图10给出了200条时长为600 s外压激励样本下瞬态内压极大值的估算结果与精确结果的对比，由图10可知，精确结果与估算结果非常接近，误差范围为0.71%～5.47%，对于工程应用来说可以接受。故文中提出的估算方法在保证精度的同时，能大大减少计算工作量，可用于估算突然开孔结构瞬态内压极值。

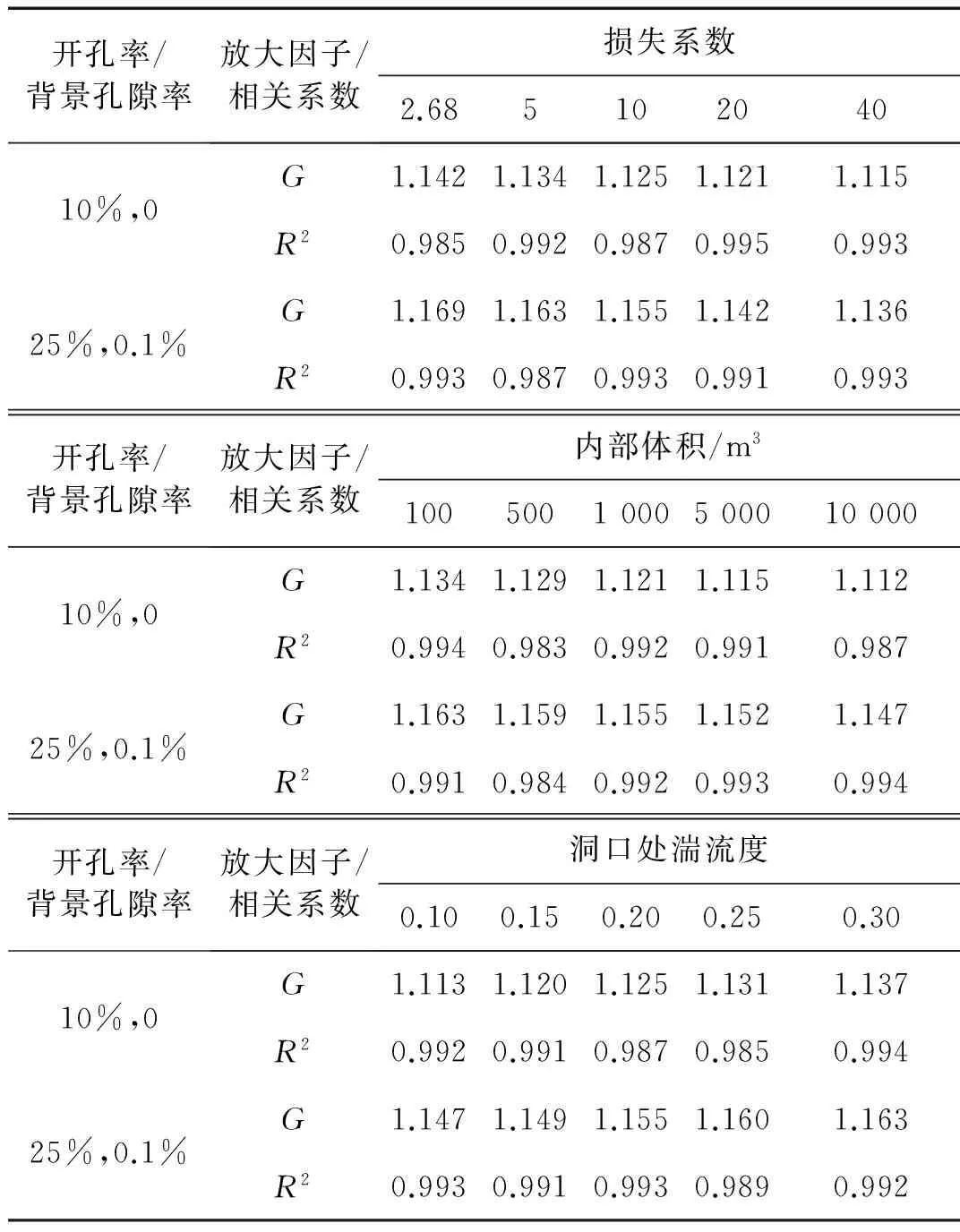
表1 放大因子拟合结果表

(a)开孔率(背景孔隙率0.1%)(b)背景孔隙率(开孔率25%)

图10 瞬态内压极大值计算结果

Fig.10 Numerical results of the maximum value of transient internal pressure

5 结 论

(1) 孔口开启时间对结构瞬态内压峰值起着控制性作用，开孔瞬间外压值越大，瞬态内压峰值越大，但两者最大值之间存在着一定的时间差。

(2) 瞬态内压极大值与瞬态内压峰值(当外压极大时开孔)之间存在着一定的比例关系，可用放大因子G对其进行定量描述，在工程涵盖范围内其变化范围不大，可近似取为1.17。

(3) 文中给出的瞬态内压极大值估算方法能在保证精度的同时避免过大的计算量，利用该方法能有效地估算突然开孔结构瞬态内压的设计值。

[1] 黄鹏, 陶玲, 全涌, 等. 浙江省沿海地区农村房屋抗风情况调研[J]. 灾害学, 2010, 25(4): 90-95.

HUANG Peng, TAO Ling, QUAN Yong, et al. Investigation of wind resistance performance of rural houses in coastal areas of Zhejiang province[J]. Journal of Catastrophology, 2010, 25(4): 90-95.

[2] SHARMA R N, RICHARDS P J. The effect of roof flexibility on internal pressure fluctuations[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 72(1/2/3): 175-186.

[3] YU S C, LOU W J, SUN B N. Wind-induced internal pressure response for structure with single windward opening and background leakage[J]. Journal of Zhejiang University Science A, 2008, 9(3): 313-321.

[4] YU X F, QUAN Y, GU M. Responses of wind-induced internal pressure in a two-compartment building with a dominant opening and background porosity Part 1: theoretical formulation and experimental verification[J]. Journal of Central South University, 2012, 19(10): 2940-2948.

[5] SABAREESH G R, MATSUI M, TAMURA Y. Characteristics of internal pressures and net local roof wind forces on a building exposed to a tornado-like vortex[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 112(1): 52-57.

[6] SHARMA R N, MASON S, DRIVER P. Scaling methods for wind tunnel modelling of building internal pressures induced through openings[J]. Wind and Structures, 2010, 13(4): 363-374.

[7] OH J H, KOPP G A, INCULET D R. The UWO contribution to the NIST aerodynamic database for wind loads on low buildings Part 3: internal pressures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(8): 755-779.

[8] STATHOPOULOS T, LUCHIAN H D. Transient wind-induced internal pressures[J]. Journal of Engineering Mechanics, 1989, 115(7): 1501-1514.

[9] 段旻, 谢壮宁, 石碧青. 低矮房屋瞬态内压的风洞试验研究[J]. 土木工程学报, 2012, 45(7): 10-16.

DUAN Min, XIE Zhuangning, SHI Biqing. A wind tunnel study of the transient internal pressure of a low rise building[J]. China Civil Engineering Journal, 2012, 45(7): 10-16.

[10] VICKERY B J, BLOXHAM C. Internal pressure dynamics with a dominant opening[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 41(1/2/3): 193-204.

[11] SHINOZUKA M, JAN C M. Digital simulation of random processes and its applications[J]. Journal of Sound and Vibration, 1972, 25(1): 111-128.

[12] YU X F, XIE Z N. Interference effects on wind pressure distribuiton for high-rise buildings[C]//The 14th International Conference on Wind Eingeering. Porto Alegre: [s.n.], 2015.

Extreme value of wind-induced transient internal pressure of buildings suffering sudden opening

YU Xianfeng1， DUAN Min2， XIE Zhuangning1

(1. State Key Laboratory of Subtropical Building Science, South China University of Technology, Guangzhou 510640, China;2. School of Civil Engineering, City College of Science and Technology, Chongqing University, Chongqing 402167, China)

Peak values of wind-induced transient internal pressure response were studied in detail when a structure’s doors/windows suddenly were broken based on the classical governing equation of internal pressure. The effects of opening time on the peak transient internal pressure were analyzed. The estimated method for extreme value of transient internal pressure of buildings suffering sudden opening was presented, it was compared with the accurate calculation method. The results showed that the larger the external pressure when a building’s doors/windows suddenly open, the larger the peak value of the transient internal pressure; however, there is a time lag between the maximum external pressure and the peak transient internal pressure; an amplification factor (G=1.17) can be used to describe the ratio of the extreme value of transient internal pressure to the peak internal pressure response when the external pressure reaches its maximum value; the presented method can be effectively used to estimate the extreme value of transient internal pressure of a building suffering sudden opening.

overshooting effect; transient internal pressure; time lag; amplification factor; wind tunnel test

国家自然科学基金(51408227);国家科技支撑计划项目(2006BAJ06B05-3)

2015-12-09 修改稿收到日期：2016-03-25

余先锋 男，博士，讲师，1985年生

谢壮宁 男，博士，教授，1963年生

TU312.1

A

10.13465/j.cnki.jvs.2017.09.010