汽车驱动桥系统模态综合动力学建模与分析

周 驰， 丁炜琦， 桂良进， 范子杰

(1.清华大学 汽车工程系 汽车安全与节能国家重点实验室，北京 100084； 2.陕西汉德车桥有限公司，西安 710201)

汽车驱动桥系统模态综合动力学建模与分析

周 驰1， 丁炜琦2， 桂良进1， 范子杰1

(1.清华大学 汽车工程系 汽车安全与节能国家重点实验室，北京 100084； 2.陕西汉德车桥有限公司，西安 710201)

提出一种汽车驱动桥系统的模态综合动力学建模与分析方法，采用非线性轴承单元实现传动系模型与桥壳模型的耦合建模，采用模态综合法对驱动桥各部件的有限元模型进行缩维变换，能够在准确模拟驱动桥系统动力学特性的同时大大缩减系统模型规模，从而快速准确地实现驱动桥系统的静力学非线性求解和动力学分析。以准双曲面齿轮有限元接触分析求得的动态啮合力作为系统激励，计算驱动桥系统的动力学响应，并进行试验验证，数值计算结果能够准确体现准双曲面齿轮动态啮合力激励下的驱动桥系统动力学特性，有效指导驱动桥的减振降噪设计。

驱动桥；模态综合法；准双曲面齿轮；动力学分析

驱动桥是汽车的核心动力总成和主要的振动噪声源，驱动桥系统的振动噪声会影响汽车的可靠性、乘员的舒适性和运输的安全性[1]。准双曲面齿轮广泛用于驱动桥主减速器传动系统，齿轮啮合过程中产生的动态激励是驱动桥系统振动噪声的主要原因[2]。现有研究大多采用集中参数模型对准双曲面齿轮系统进行动力学建模与分析[3-5]，对桥壳和轴承等部件的模拟过于简化，无法准确体现驱动桥系统的动力学特性。有学者采用有限元接触分析方法计算驱动桥系统的动态响应，但驱动桥有限元模型包含大量接触关系，建模过程十分复杂，系统模型的规模巨大，接触分析需要消耗大量的计算资源，分析效率和收敛性很低[6]。另有学者在驱动桥系统有限元建模时对滚动轴承模型进行了简化，无法准确体现滚动轴承的非线性刚度特性[7-8]。

周驰等提出了一种基于空间梁单元理论的驱动桥系统动力学建模分析方法，并采用非线性滚子轴承单元实现了传动系与桥壳模型的耦合建模，能够快速实现驱动桥系统的动力学分析，但空间梁单元模型对齿轮轮齿和十字轴等局部特征进行了等效，且采用的传统等效啮合模型求得的准双曲面齿轮啮合参数没有考虑齿面摩擦的影响，动力学分析时采用的单位谐波传动误差激励较为简化，建模和分析的精度有待进一步提高。本文在文献[9]的基础上，提出一种更准确和通用的汽车驱动桥系统模态综合动力学建模和分析方法，建立更为准确的驱动桥系统动力学分析模型，并以准双曲面齿轮有限元接触分析求得的动态啮合力作为系统的激励源，准确计算驱动桥系统的动力学响应，并进行试验验证。

1 驱动桥系统部件有限元建模

图1为典型商用车后驱动桥的几何模型，发动机后置，规定前进方向为全局坐标系X轴的正向，左侧为Y轴的正向，竖直向上为Z轴的正向，坐标原点O取在轮间差速器的十字轴中心位置。图2为驱动桥传动系的二维示意图。

图1 驱动桥几何模型

1-差速器左侧圆锥滚子轴承；2-左半轴；3-左车轮；4-左输出转矩；5-左输出端扭转刚度；6-左输出端转动惯量；7-左车轮外侧圆锥滚子轴承；8-左车轮内侧圆锥滚子轴承；9-左太阳轮；10-行星轮；11-小轮轴；12-输入端扭转刚度；13-输入端转动惯量；14-输入转矩；15-传动轴凸缘；16-小轮轴后端圆锥滚子轴承；17-小轮轴中部圆锥滚子轴承；18-小轮轴前端圆柱滚子轴承；19-右太阳轮；20-右半轴；21-右车轮内侧圆锥滚子轴承；22-右车轮；23-右车轮外侧圆锥滚子轴承；24-右输出端转动惯量；25-右输出端扭转刚度；26-右输出转矩；27-差速器右侧圆锥滚子轴承；28-差速器壳；29-大轮；30-十字轴

图2 驱动桥传动系示意图

Fig.2 Schematic of drive axle transmission system

1.1 传动系部件有限元模型

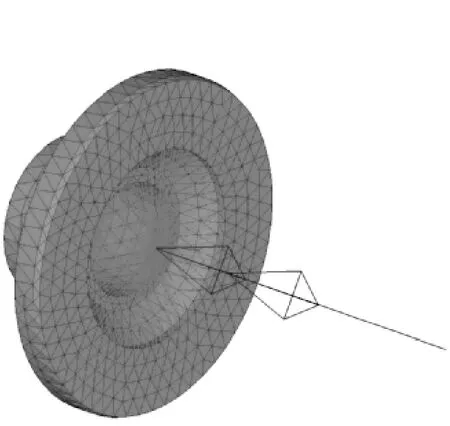
建立传动系部件的体单元有限元模型，如图3～图9所示，单元类型为四节点四面体单元，材料参数为部件的真实材料参数。为了实现后续模态综合缩维计算和模型之间的连接，需要在有连接关系的位置建立边界节点，以边界节点作为主节点，采用刚性连接单元(RBE2)与部件有限元模型的体单元节点耦合。传动系各部件的边界节点建立如下：

(1) 传动轴凸缘模型建立两个边界节点，如图3所示，1号节点为花键连接节点，2号节点为输入转矩加载点；

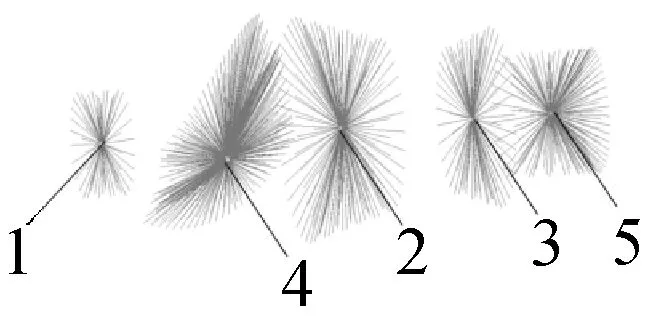
(2) 小轮轴模型建立5个边界节点，如图4所示，1号～3号节点为轴承连接点，4号节点为齿轮等效啮合节点，5号节点为花键连接节点；

(a) 有限元模型

(b) 边界节点

(a) 有限元模型

(b) 边界节点

(a) 有限元模型

(b) 边界节点

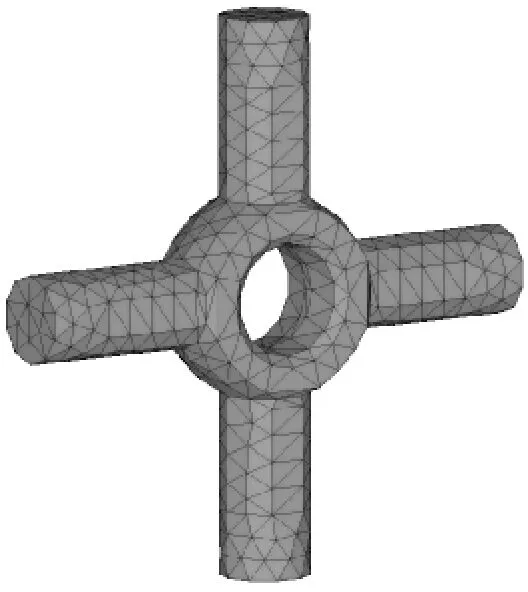
图5 大轮及差速器壳模型

Fig.5 Finite element models of wheel and differential case

(a) 有限元模型

(b) 边界节点

(a)有限元模型(b)边界节点

(3) 大轮与差速器壳模型采用共用节点的方法连接，用来模拟螺栓连接，建立9个边界节点，如图5所示，1号和2号节点为轴承连接节点，3号节点为准双曲面齿轮等效啮合节点，4号和5号节点为垫片连接节点，6号～9号节点为差速器壳十字轴孔连接节点；

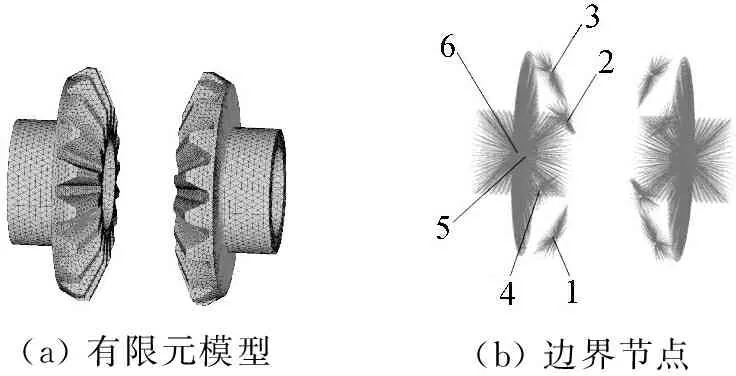
(4) 十字轴模型建立8个边界节点，如图6所示，1号～4号节点为行星轮旋转副连接节点，5号～8号节点为差速器壳十字轴孔连接节点；

(a)有限元模型(b)边界节点

图8 太阳轮模型

图9 半轴及轮毂模型

Fig.9 Finite element models of half shafts and hubs

(5) 差速器共有4个行星轮，每个行星轮模型建立3个边界节点，如图7所示，1号和2号节点为等效啮合节点，3号节点为旋转副连接节点；

(6) 每个太阳轮模型建立6个边界节点，如图8所示，1号～4号节点为等效啮合节点，5号节点为花键连接节点，6号节点为差速器壳垫片连接节点；

(7) 半轴与车轮模型采用共用节点的方式连接，用来模拟螺栓连接，左右两侧模型均建立4个边界节点，如图9所示，1号和2号节点为轴承连接节点，3号节点为花键连接节点，4号节点为输出转矩加载点。

1.2 桥壳有限元模型

桥壳有限元模型如图10所示，在9个滚动轴承的中心位置均建立边界节点，并分别通过刚性连接单元与轴承座表面的节点耦合。为了与试验对比，在加速度测点位置也建立边界节点。约束板簧位置的节点自由度，模拟振动试验台对桥壳的支承。

图10 桥壳有限元模型

1.3 非线性滚动轴承模型

滚动轴承是连接传动系和桥壳的关键部件，采用非线性轴承单元[10]耦合对应的传动系模型边界节点自由度与桥壳边界节点自由度，如图11所示。

图11 滚动轴承模型示意图

1.4 齿轮啮合模型

本文驱动桥为准双曲面齿轮传动，齿轮参数如表1所示，采用有限元分析软件ABAQUS建立准双曲面齿轮有限元接触分析模型[11-13]，如图12所示，对5对齿轮进行接触分析即可求得准双曲面齿轮一个啮合周期的等效啮合参数[14]。根据试验转矩工况，在小轮模型中心施加转矩Tp=-1 257 N·m，齿面摩擦因数取0.1[15]，求得的准双曲面齿轮等效啮合参数如表2所示。

表1 准双曲面齿轮参数

图12 准双曲面齿轮有限元模型

参数X分量Y分量Z分量等效啮合点坐标/mm-180.97-14.2417.67等效啮合力方向向量0.535-0.5640.629等效啮合刚度/(MN·mm-1)1.628

差速器齿轮的等效啮合参数采用文献[9]中的方法求得。基于齿轮等效啮合参数，可以进一步计算齿轮的啮合刚度矩阵。

有限元接触分析求得的大轮动态啮合力如图13所示，小轮动态啮合力与大轮大小相等，方向相反，该动态啮合力即为驱动桥系统动力学分析的激励源。

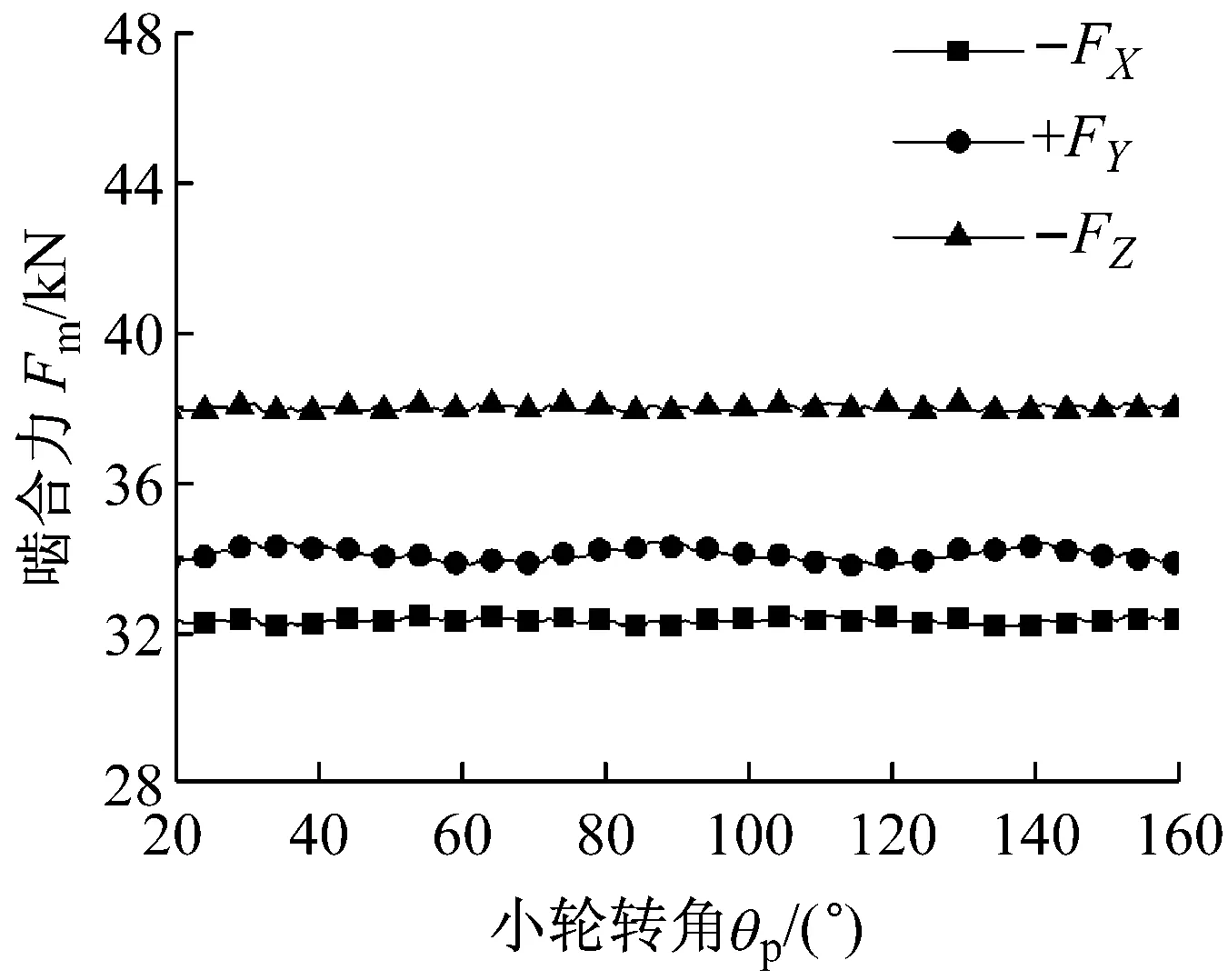
图13 准双曲面齿轮等效啮合力

1.5 连接部件模型

对传动系部件之间的连接关系进行模拟，包括：传动轴凸缘与小轮轴之间的花键连接、太阳轮与半轴之间的花键连接、十字轴与差速器壳十字轴孔之间的连接、十字轴与行星轮之间的旋转副连接、太阳轮与差速器壳之间的垫片连接。上述连接关系均采用线性弹簧单元模拟，刚度矩阵表示为式(1)的形式

Kc=diag([kδXkδYkδZkθXkθYkθZ])

(1)

式中:kδX、kδY和kδZ为各方向的平动刚度；kθX、kθY和kθZ为各方向的转动刚度。

2 驱动桥系统模态综合动力学建模

采用固定界面模态综合法[16]对各部件的有限元模型进行缩维，仅保留边界节点自由度和体现内部节点自由度振动特性的主模态自由度，有限元模型缩维后的模态综合刚度矩阵KM和模态综合质量矩阵MM如式(2)和式(3)所示

(2)

(3)

式中:KFE和MFE分别为原始有限元模型的刚度矩阵和质量矩阵；kcc为边界自由度对应的刚度矩阵；knc和kcn为边界自由度与主模态自由度之间的刚度耦合项；knn为主模态自由度对应的刚度矩阵；mcc为边界自由度对应的质量矩阵；mnc和mcn为边界自由度与主模态自由度之间的质量耦合项；mnn为主模态自由度对应的质量矩阵；Φ为模态综合变换矩阵，如式(4)所示

(4)

假设部件A与部件B的模态综合模型之间存在连接关系，连接单元的刚度矩阵为KC，则边界节点自由度刚度项KA和KB的耦合关系如式(5)所示

(5)

由式(5)的方法将各部件的刚度矩阵和质量矩阵按照连接关系组集，获得驱动桥系统的刚度矩阵K和质量矩阵M，完整驱动桥系统模态综合模型的动力学方程如式(6)所示

(6)

由于滚动轴承单元具有非线性特性，将对应转矩工况静平衡时的轴承切线刚度矩阵作为动力学模型的线性轴承刚度。

完整驱动桥系统的有限元模型共包含235 150个节点，而本文建立的驱动桥系统模态综合动力学模型共有1 034个自由度，自由度大幅度减小，对比模态综合模型与有限元模型求得的驱动桥系统2 000 Hz以内的固有振动频率，最大相对误差为4.99%，大部分在2%以内，说明驱动桥模态综合动力学模型良好地保留了原有限元模型的动力学特性。

3 驱动桥系统动力学分析与试验验证

采用有限元接触分析方法求得的主减速器齿轮动态啮合力在一个周期内的离散数据可以表示为式(7)所示傅里叶级数形式

(7)

(8)

式中:zp为小轮齿数；np为小轮转速,r/min；频率的单位为Hz。

60 km/h车速试验工况对应的输入转速np=1 671 r/min，由式(8)求得准双曲面齿轮基频f0=195 Hz。对图13中的一个周期啮合力数据进行式(7)所示的傅里叶级数变换，求得各阶齿轮激振频率对应的啮合力幅值A和相位B如图14和图15所示，傅里叶变换求得的直流分量即为等效啮合力的平均值，X、Y、Z三个方向的直流分量分别为32.28 kN、34.04 kN和37.96 kN。

图14 准双曲面齿轮等效啮合力幅值

图15 准双曲面齿轮等效啮合力相位

(9)

式中:ω和φ分别为驱动桥系统的固有振动圆频率和正则振型；ωdk为齿轮啮合力第k阶激振圆频率；ωi为驱动桥系统的第i阶固有振动圆频率；λi=ωdk/ωi为第i阶频率比；ξi为第i阶模态阻尼比，计算时取0.02；n为模态叠加法保留的驱动桥系统模态阶数。

驱动桥系统总位移响应即为式(9)各阶响应的叠加，如式(10)所示

(10)

式中，NF为动态啮合力包含的频率阶数。

测量驱动桥在稳定运转过程中桥壳上的加速度响应，在桥壳顶部和后盖分别布置加速度传感器，如图16所示，试验工况为60 km/h车速滑行工况，输入转矩Tp=-1 257 N·m，输入转速np=1 671 r/min。

图16 驱动桥振动响应试验

对比本文数值计算与试验测得的时域法向振动加速度曲线如图17和图18所示，结果较为一致。

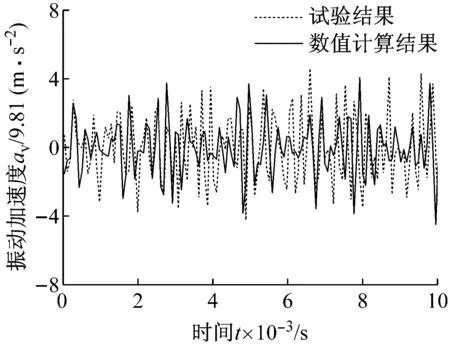
图17 桥壳上方测点法向振动加速度

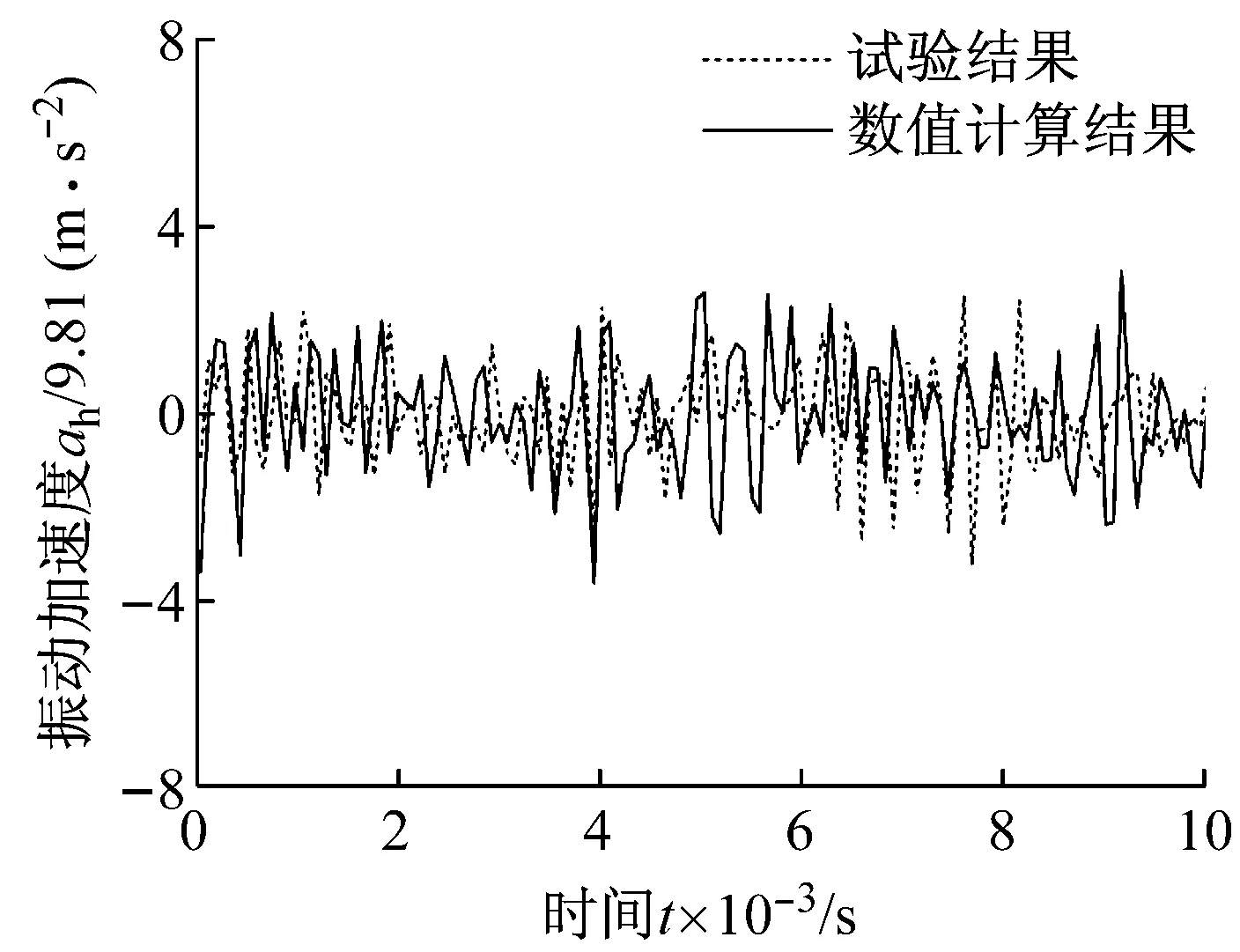
图18 后盖测点法向振动加速度

进一步对比上述时域振动加速度的均方根值，如表3所示，数值计算结果与试验结果的相对误差在15%左右，吻合程度较为理想，验证了本文驱动桥系统动力学建模和分析方法的正确性。

表3 振动加速度均方根值

振动加速度的幅值谱分析结果如图19和图20所示， 因为主减速器齿轮的动态啮合激励是驱动桥系统振动噪声的最主要原因，数值计算与试验结果均较为明显地体现出准双曲面齿轮啮合激励的基频和倍频成分，且一致性良好。

图19 桥壳上方法向振动加速度幅值谱

Fig.19 Vibration acceleration amplitude spectrum on the top of the housing

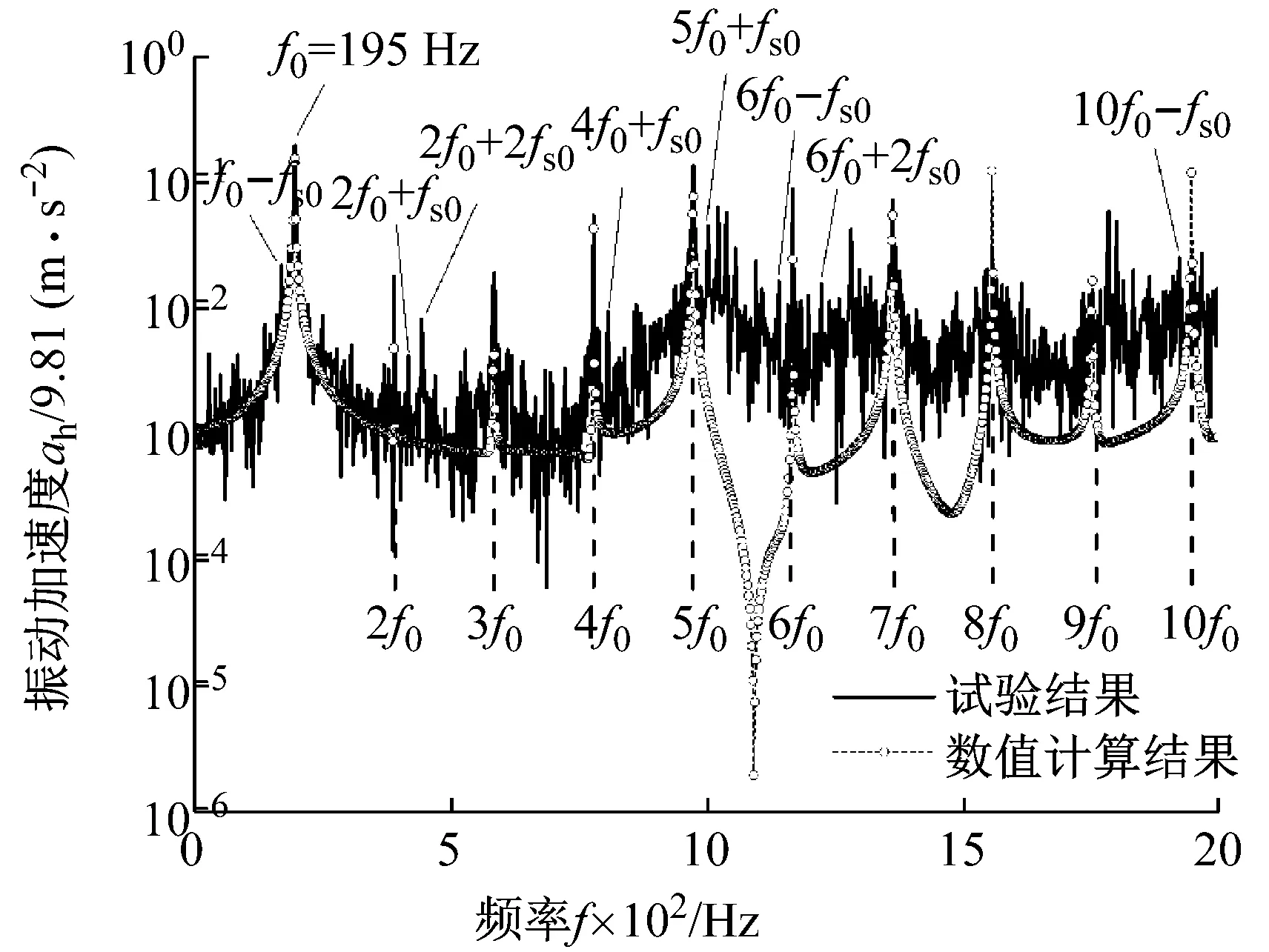
图20 后盖测点法向振动加速度幅值谱

Fig.20 Vibration acceleration amplitude spectrum on the rear cover

在试验过程中，如果输入轴不平衡，也会对驱动桥系统产生动态激励，输入轴不平衡激振的基频fs0如式(11)所示，ns为输入轴的转速，r/min，60 km/h车速工况对应的fs0为27.85 Hz。

(11)

在图19和图20中的试验振动加速度幅值谱分析结果中，输入轴不平衡激励主要以齿轮激振频率和输入轴激振频率的组合形式体现，图19中可以观察到f0-fs0、5f0+fs0、6f0-fs0、6f0+fs0、6f0+2fs0、7f0-fs0和10f0-fs0等组合频率峰值，图20中可以观察到f0-fs0、2f0+fs0、2f0+2fs0、4f0+fs0、5f0+fs0、6f0-fs0、6f0+fs0、6f0+2fs0和10f0-fs0等组合频率峰值。

4 结 论

本文通过汽车驱动桥系统的模态综合动力学建模与分析，获得如下结论：

(1) 提出了一种驱动桥系统模态综合动力学建模和分析方法，能够在准确模拟驱动桥系统动力学特性的同时大大缩减系统模型规模，以有限元接触分析方法求得的准双曲面齿轮动态啮合力作为驱动桥系统的激励源，能够准确实现驱动桥系统的动力学分析。

(2) 驱动桥壳体测点的振动加速度数值计算结果与试验结果吻合良好，验证了本文方法的正确性，振动加速度幅值谱的峰值频率能够良好地体现出准双曲面齿轮啮合激励特性。

(3) 本文方法基于可靠的理论基础，且易于通过商用软件和编程实现，具有较高的计算效率，能够准确快速地实现驱动桥系统的动力学建模与分析，有效指导驱动桥的减振降噪设计，并可广泛用于其他齿轮传动系统的设计建模与计算分析。

[1] 刘惟信. 汽车车桥设计[M]. 北京: 清华大学出版社，2004:5-22.

[2] DONLEY M G, LIM T C, STEYER G C. Dynamic analysis of automotive gearing systems[C]// Detroit： SAE International Congress and Exposition, 1992:77-87.

[3] LIM T C, CHENG Y. A theoretical study of the effect of pinion offset on the dynamics of hypoid geared rotor system[J]. Journal of Mechanical Design, 1999, 121(4):594-601.

[4] CHENG Y, LIM T C. Vibration analysis of hypoid transmissions applying an exact geometry-based gear mesh theory[J]. Journal of Sound and Vibration, 2001, 240(3):519-543.

[5] CHENG Y, LIM T C. Dynamics of hypoid gear transmission with nonlinear time-varying mesh characteristics[J]. Journal of Mechanical Design, 2003, 125(2):373-382.

[6] 郭年程, 史文库, 刘文军, 等. 驱动桥的整体有限元动态模拟[J]. 西安交通大学学报, 2012, 46(9):91-95.

GUO Niancheng, SHI Wenku, LIU Wenjun, et al. Dynamic simulation of driving axle based on finite element method[J]. Journal of Xi’an Jiaotong University, 2012, 46(9):91-95.

[7] 张健. 汽车驱动桥振动噪声研究[D]. 重庆: 重庆大学, 2005.

[8] 晏慧. 重型商用车驱动桥振动噪声预测研究[D]. 重庆: 重庆大学, 2010.

[9] 周驰, 丁炜琦, 桂良进, 等. 一种驱动桥齿轮传动系统动力学建模与分析方法[J]. 振动与冲击, 2015, 34(15):188-194.

ZHOU Chi, DING Weiqi, GUI Liangjin, et al. Dynamic modeling and analysis for drive axle gear transmission system[J]. Journal of Vibration and Shock, 2015, 34(15):188-194.

[10] 田程, 周驰, 桂良进, 等. 考虑轴承刚度耦合性和非线性的多支撑轴系有限元分析方法[J]. 机械工程学报，2015, 51(17):90-95.

TIAN Cheng, ZHOU Chi, GUI Liangjin, et al. A method of finite element analysis for multi-support shaft system base on the coupling and nonlinearity of bearing stiffness[J]. Journal of Mechanical Engineering, 2015, 51(17):90-95.

[11] LITVIN F L, ZHANG Y. Local synthesis and tooth contact analysis of face-milled spiral bevel gears: ARL-CR-312[R]. Illinois: University of Illinois at Chicago, 1991.

[12] LITVIN F L, FUENTES A. Gear geometry and applied theory[M]. 2nd ed. Cambridge: Cambridge University Press, 2004:679-696.

[13] Stiffness calculations based on the finite element method[J]. Journal of Mechanical Engineering, 2011, 47(11): 23-29.

[14] PENG T. Coupled multi-body dynamic and vibration analysis of hypoid and bevel geared rotor system[D]. Cincinnati: University of Cincinnati, 2010.

[15] HARRIS T A, KOTZALAS M N. Essential concepts of bearing technology[M]. 5th ed. Beijing: CRC Press, 2006:86.

[16] CRAIG R R, BAMPTON M C C. Coupling of substructures for dynamic analyses[J]. AIAA Journal, 1968, 6(7):1313-1319.

Modal synthesis dynamic modeling and analysis for an automotive drive axle system

ZHOU Chi1, DING Weiqi2, GUI Liangjin1, FAN Zijie1

(1. State Key Laboratory of Automotive Safety and Energy, Department of Automotive Engineering, Tsinghua University, Beijing 100084, China; 2. Shaanxi Hande Axle Co., Ltd., Xi’an 710201, China)

A modal synthesis dynamic modeling and analysis method for an automotive drive axle system was proposed. The transmission system model and the housing model were coupled with nonlinear bearing elements. In order to realize static nonlinear solving and dynamic analysis of the drive axle system quickly and accurately, finite element models of its components were condensed with the modal synthesis method. Meshing forces of a couple of hypoid gears were calculated based on the finite element contact analysis method. The dynamic responses of the drive axle system excited by the meshing forces of the couple of hypoid gears were calculated and verified with tests. The numerical analysis results revealed the dynamic characteristics of the drive axle system under the excitation of the meshing forces of the couple of hypoid gears correctly and guided the vibration and noise reduction design of the drive axle effectively.

drive axle; modal synthesis method; hypoid gear; dynamic analysis

校企合作项目(20142000237)

2016-01-15 修改稿收到日期：2016-03-15

周驰 男，博士，1986年生

范子杰 男，教授，博士生导师，1958年生

TH132.46；U463.218

A

10.13465/j.cnki.jvs.2017.09.002