考虑背景孔隙的单开孔两空间结构的风致内压响应研究

余先锋， 顾 明， 全 涌， 樊友川

（同济大学 土木工程防灾国家重点实验室，上海200092）

0 引 言

建筑结构的风荷载不仅取决于结构外表面的风压分布，内压的作用也不容忽视。一些重要结构，如大型机库、机场航站楼、外覆玻璃幕墙的高层建筑等，它们在结构抗风设计时必须要考虑内压的作用。强风中由于风致飞掷物的撞击，门窗突然破坏，气流涌入室内，导致结构内部脉动内压增大，结构在内外压共同作用下发生破坏的情况时有发生［1－2］。

当结构内部无明显的通风效应，可认为内压在空间上是完全相关的。在此前提下，可采用空气动力学的理论方法来研究内压，其中内压控制方程是理论研究的基础。自从 Homles（1979）［3］首次采用类似于Helmholtz声学共振器原理导出了一个二阶非线性微分方程，并以此来描述带有主开洞建筑物的风致脉动内压后，各国风工程学者在考虑背景孔隙（例如通风孔、墙壁小裂缝等，如图1所示）、结构内部空间等因素后对内压控制方程进行了修正与完善。Vickery（1992）［4］通过风洞试验研究发现背景孔隙增大了内压振荡的阻尼，减小了瞬态与常态开洞的内压共振响应；余世策（2006）［5］推导了考虑背景孔隙后的单空间开孔结构的内压响应方程；Sharma（2003）［6］研究了结构内部空间对内压响应的影响，并给出了两空间结构内压响应的线性控制方程组，但未考虑背景孔隙的影响。

本文仍以一个带有主开洞的两空间结构为研究对象，通过合理假定，从非定常形式的伯努利方程、气体质量守恒定律和绝热气体状态方程等推导了单开孔两空间结构在考虑背景孔隙后的内压响应控制方程组，完善了两空间结构的内压理论。通过数值参数分析，采用常压激励研究了无背景孔隙时的内压响应时程及其幅频特性，采用强迫激振法研究了内压响应均方根值及内压增益的变化规律；进而采用强迫激振法研究了背景孔隙对内压响应时程、幅频特性与内压增益的影响，着重分析了背景孔隙总面积与两子空间的内压响应之间的关系。研究成果对结构风致内压有理论与实际应用的价值。

1 考虑背景孔隙后的内压控制方程组

1.1 基本假定

本文研究的两空间结构，其迎风墙面与隔墙上各存在单一开洞，且洞口尺寸远大于单个背景孔隙。这里假定存在背景孔隙的两空间开孔结构满足如下合理假定：

（1）结构为刚性结构，即忽略结构柔度对内压脉动的影响；

（2）各子空间的内压在各自空间上完全相关，这是内压响应理论的前提条件，且已得到实验证实［3］；

（3）各子空间的空气均符合绝热定律，即控制内部气体压强与密度变化的状态方程为：

式中：γ为等压过程和等容过程的气体比热之比，一般取γ＝1.4；Pi、ρi分别为内部气体压强与密度；对式（1）两边取微分并作化简，可得：

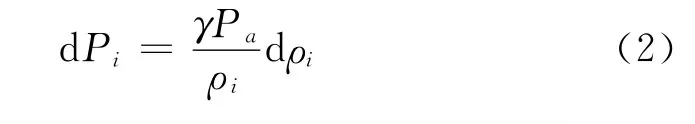
式中：Pa为大气压，即稳态时的结构内部压强；

（4）单个背景孔隙面积很小，因此孔隙中的“气塞”质量也很小，但此时墙厚作用增加，阻尼较大［7］，故与阻尼效应相比，可忽略背景孔隙处泄漏气体的惯性效应；

（5）结构背风面平均风压相近［8］，与结构内压脉动相比，背风面风压脉动不大，故可忽略背风面的风压脉动，以同一个平均风压系数来考虑背风面的风压。

1.2 控制方程组

带背景孔隙的两空间开孔结构风致内压响应的简化模型如图1所示。由非定常形式的伯努利方程［9］（非定常流动的伯努利方程，相比定常流动增加一个与加速度有关的项），可得迎风墙与子空间1的两侧瞬态气压差与其洞口处气流速率的关系为：

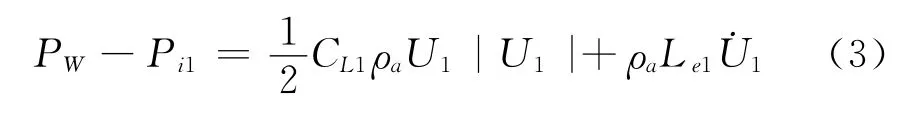
类似地，子空间1与子空间2两侧瞬态气压差与洞口处气流速率的关系为：

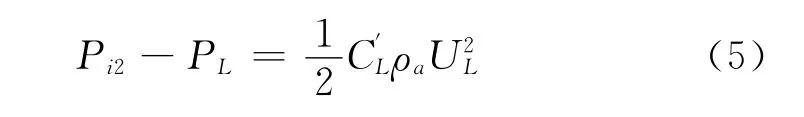
式中，PW、Pi1、Pi2和PL分别为迎风墙面、子空间1、子空间2及背风面的瞬态风压；U1、U2和UL分别为开洞1、开洞2及背景孔隙处的气流速率；Le1、Le2分别为开洞1与开洞2处的气柱有效长度；CL1、CL2和C′L分别为开洞1、开洞2及背景孔隙处的损失系数。

由假设（4）可得，背风面孔隙泄漏处的空气流速与孔隙两侧气压差的关系为：

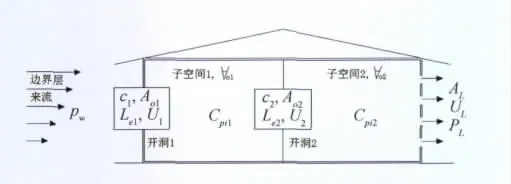
图1 带有背景孔隙的开孔两空间结构模型Fig.1 Model of building with internal partitioning，openings and background porosity

等式（5）两边同时除以1／2ρaU，并结合假设（5）可得：

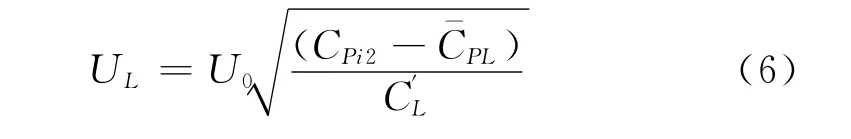
对式（6）两边求导可得：

式中，CPi2为子空间2的瞬态内压系数L为背风面平均风压系数，风压系数均以来流风速U0为参考风速。

式中，Ao1、Ao2分别为开洞1与开洞2的面积，AL为背风面孔隙面积之和；c1、c2分别为开洞1、开洞2的气流收缩流动系数，∀o1和∀o2为子空间1、2的体积。由假设（1）（3）可得结构内部体积不变，气流涌进结构后，使得结构内部空气压缩，其密度发生改变，由气体绝热定律可得空气密度变化与压强变化的关系，如式（2）所示。

将式（2）代入式（8）与式（9）可得：

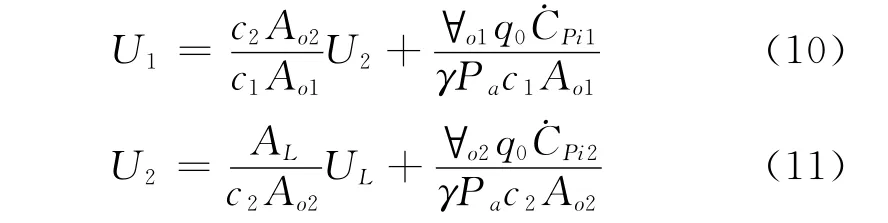
式中q0＝ρa，为来流参考风压。对式（10）与式（11）分别求导可得：

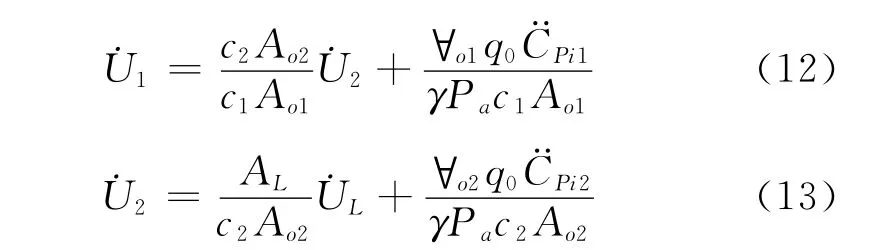
将式（6、7）及式（10～13）代入式（3、4）可得考虑背景孔隙后的两空间结构的内压控制方程组为：

当背景孔隙为零时，即AL＝0，式（14）与式（15）将化为：

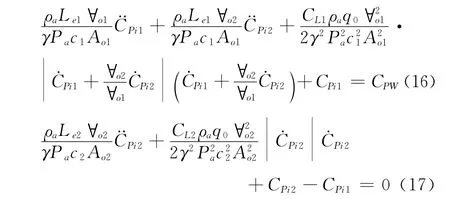
若将式（16）与式（17）的阻尼线性化后，它即为Sharma（2003）［6］提出的两空间结构的内压控制方程组。

2 数值参数分析

上文从理论上推导了单开孔两空间结构在考虑背景孔隙后的内压响应控制方程组，为清楚地描述背景孔隙对内压响应的影响，本节将对推导的内压响应方程组进行数值求解与分析。本内压系统所取的基本参数如下：

2.1 无背景孔隙时的内压响应分析

无背景孔隙的内压响应是研究有背景孔隙的内压响应的基础，故首先进行无背景孔隙的内压响应分析是必要的。

取上述基本参数后，并使CPW＝1。通过龙格－库塔法对式（16、17）求解，可得两子空间的内压响应时程，如图2（a）所示，相应的幅频特性如图2（b）所示。由图2（a）可知，两子空间的内压响应均为自由振动衰减过程；从图2（b）可以看出，两子空间的内压响应幅值的峰值所对应的频率为2.45Hz与6.06Hz。

其实Sharma（2003）［6］已研究了无背景孔隙的两空间结构的内压响应，给出了内压导纳的理论表达式，并指出有阻尼的内压自振频率与无阻尼的内压自振频率很接近，即内压系统本身的阻尼是比较小的。当无阻尼时，内压导纳如式（18、19）所示：

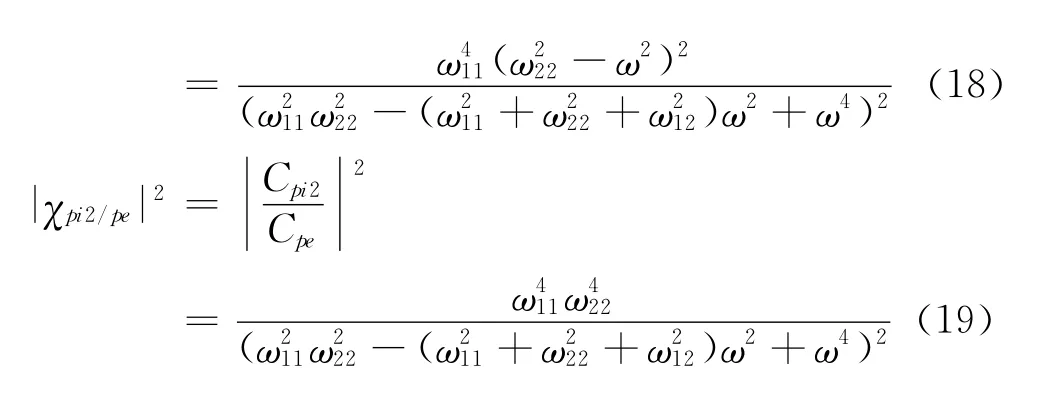
为得到内压的均方根值与增益函数，可采用强迫激振法［5］来分析内压响应，定义外压系数满足如下正弦曲线形式：

式中，｜Cpe｜为外压系数脉动幅值，f为激振频率。

取上述基本参数后，并使｜Cpe｜＝0.3，f＝1。通过龙格－库塔法对式（16、17）求解，待内压响应达到稳态后，可得两子空间的内压系数均方根值随体积比∀o1／（∀o1＋∀o2）的变化曲线，如图3（a）所示。从图3（a）可知，在各种体积比下，子空间2的内压系数均方根值都大于子空间1，这与Sharma（2003）［6］所得到的结论是一致的。

当∀o1／（∀o1＋∀o2）＝0.6时，两子空间的内压增益随外部激励频率的变化曲线如图3（b）所示。从图3（b）中可以看出，随着外部激励频率的变化，两子空间的内压增益函数均表现出两个共振峰值，峰值对应的频率为2.3Hz与5.9Hz。这是因为内压增益函数是内压系统本身的属性，与外界激励等无关，故对于这样的类似于结构动力学中的两自由度系统，其两个共振频率分别对应于两子空间的内压自振频率，而外部激励频率不会体现于内压增益曲线中；另外，内压增益曲线图中两峰值对应的频率值与从导纳函数理论表达式得到的内压系统的自振频率是吻合的，这也进一步证明了强迫激振法对两空间开孔结构的内压响应分析的适用性。

2.2 背景孔隙对内压响应的附加影响分析

在考虑了背景孔隙这一因素后，内压响应方程变得极为复杂，各子空间内压系统的阻尼项均受到背景孔隙的影响，也不能再从理论上导出相应的内压导纳（或增益）函数表达式。上节通过对无背景孔隙的两空间结构内压响应进行理论与强迫激振法分析，证明了强迫激振法可以很好地用于两空间结构的内压响应分析，于是在考虑背景孔隙后，亦采用强迫激振法来研究内压响应。

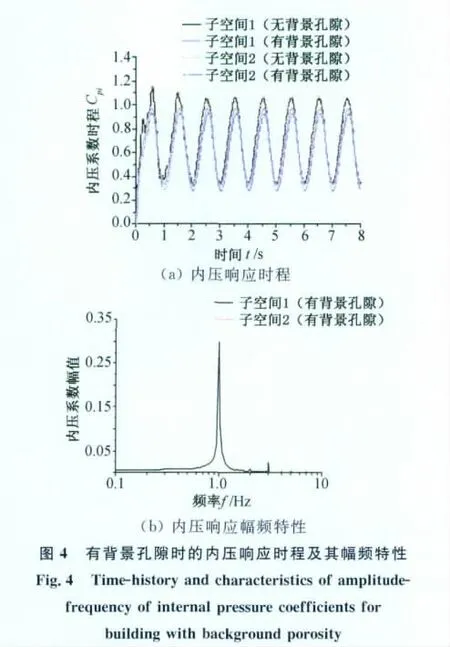
仍使外压系数满足如式（20）的正弦形式，其中取｜Cpe｜＝0.3且f＝1Hz；内压系统的基本参数也如前所述。通过龙格－库塔法对式（14、15）与式（16、17）求解可得有、无背景孔隙两种情况下的两子空间内压系数时程，如图4（a）所示；待内压达到稳态时，两子空间内压幅频特性曲线极为相似，如图4（b）所示。从图4（a）可知，未考虑背景孔隙时，子空间2的内压响应比子空间1大，而考虑背景孔隙后，子空间2的内压响应反而比子空间1略小些，且两子空间的内压振动形式均与外部激励形式相似；这是由于增加了背景孔隙后，使得内压系统的附加阻尼大为增加，从而抑制了内压响应的脉动而导致的，其中背景孔隙对子空间2内压脉动的抑制更强烈。从图4（b）可更加清楚地看到，两子空间的内压响应频率均为1Hz，与外加正弦激励的频率一致，表现为受迫振动，故两子空间内压均以正弦形式响应。另一方面，由于背景孔隙所引入的附加阻尼，抑制了两洞口“气塞”的自由振动，使得两子空间的内压稳态响应均为受迫振动，故其幅频曲线上未表现出两子空间的内压自振频率。

当背景孔隙总面积与主开洞1的面积之比AL／Ao1＝0.01时，即背景孔隙总面积很小时，两空间的内压增益如图5（a）所示。从图5（a）可知，两子空间的内压增益均表现出两个峰值，其对应的频率为两子空间内压振荡的自振频率，但此时子空间2的内压响应大于子空间1。这是由于背景孔隙太小，与无背景孔隙时的内压响应规律类似。从图3（b）与图5（a）均可发现，在第2个共振频率前，子空间2的内压响应明显大于子空间1，但在第2共振频率后，子空间2的内压响应却略小于子空间1；这与Sharma（2003）［6］通过风洞试验测得的两子空间内压导纳（如图3c）所表现的规律是一致的。

两子空间在不同面积的背景孔隙下的内压增益随频率变化的曲线如图5（b）与图5（c）所示。从图5（b）与5（c）中可以清楚地看到，随着背景孔隙总面积的增大即阻尼越来越大，两子空间的内压增益在共振频率处的峰值均越来越小，即内压响应越来越小。比较图5（b）与图5（c）可知，子空间2由于直接受到背景孔隙的影响，其内压响应受背景孔隙总面积大小的影响也更大。

3 结 论

内压控制方程是进行结构风致内压研究的基础，本文通过合理化的假定，推导了两空间开孔结构在考虑背景孔隙后的内压响应控制方程组，完善了两空间开孔结构的内压理论。通过数值算例，采用常压激励分析了无背景孔隙时的内压响应时程及其幅频特性，通过强迫激振法研究了内压响应均方根值及内压增益的变化规律；进而讨论了背景孔隙对内压响应时程、幅频特性与内压增益的影响，着重分析了背景孔隙总面积与两子空间的内压响应之间的关系。得到了如下的一些结论：

（1）本文推导的内压响应控制方程组可很好地用于分析带有背景孔隙的单开孔两空间结构的内压响应。

（2）无背景孔隙时，内侧空间（子空间2）的内压响应要高于外侧房间（子空间1）。

（3）有背景孔隙时，其附加阻尼使得两房间的内压响应均受到抑制。

（4）随着背景孔隙的增大，内侧空间（子空间2）的内压响应受到的抵制更大。

［1］孙炳楠，傅国宏，陈鸣，等.94年17号台风对温州民房破坏的调查［J］.浙江建筑，1994，4：19－23.

［2］SHANMUGASUNDARAM J，ARUNACHALAM S，COMATHINAYAGAM S，et al.Cyclone damage to buildings and structures－a case study［J］.JournalofWindEngineeringandIndustrialAerodynamics，2000，84（3）：369－380.

［3］HOLMES J D.Mean and fluctuating internal pressures induced by wind［C］.Proceedings of the 5th Int Conf on Wind Engineering，Fort Collins，USA，1979.

［4］VICKERY B J，BLOXHAM C.Internal pressure dynamics with a dominant opening［J］.JournalofWindEngineeringandIndustrialAerodynamics，1992.41－44：193－204.

［5］余世策，楼文娟，孙炳楠，等.背景孔隙对开孔结构风致内压响应的影响［J］.土木工程学报，2006，39（6）：6－11.

［6］SHARMA R N.Internal pressure dynamics with internal partitioning［C］.Proceedings of the 11th Int Conf on wind Engineering，2003.

［7］OH J H，KOPP G A，INCULET D R.The UWO contribution to the NIST aerodynamic database for wind loads on low buildings：Part 3.Internal pressures［J］.JournalofWindEngineeringandIndustrialAerodynamics，2007，95（8）：755－779.

［8］HOLMES J D.Wind loading of structures［M］.USA：Taylor ＆Francis Group，2007：87－88.

［9］VICKERY B J.Gust－factors for internal pressures in low rise buildings［J］.JournalofWindEngineeringand IndustrialAerodynamics，1986，23：259－271.