含裂纹故障的齿轮系统动力学特性研究及其故障特征分析

王 旭, 伍 星, 肖正明, 曹永立， 刘 韬

(1.昆明理工大学 机电工程学院，昆明 650500； 2.昆明云内动力股份有限公司，昆明 650500)

含裂纹故障的齿轮系统动力学特性研究及其故障特征分析

王 旭1, 伍 星1, 肖正明1, 曹永立2， 刘 韬1

(1.昆明理工大学 机电工程学院，昆明 650500； 2.昆明云内动力股份有限公司，昆明 650500)

考虑齿轮的时变啮合刚度、传动误差和轴承支撑刚度的影响，建立含齿根裂纹故障的齿轮系统多自由度力学模型，基于动力学方法对其故障机理进行研究。通过材料力学的方法计算齿轮在正常和含裂纹两种情况下的啮合刚度，对比两种刚度曲线的变化趋势，便于进行精确的动力学特性分析;对建立的模型求解系统的动态响应，结果表明当齿根存在裂纹时，其时域波形中会出现周期性的冲击现象，频谱中在啮合频率的基频及其倍频等地方形成一系列等间隔的边频谱线，其间隔大小等于故障齿轮的转频;这些边频成分幅值较低，能量分散且分布不均匀，在不同频带的幅值大小存在差异。针对上述特点，通过正交小波包方法对信号的频带进行分解，应用倒频谱分析各子频带信号的边频成分;结果表明，该方法能够有效的提高信号的信噪比，有助于识别和提取信号中由裂纹故障引起的边频成分。

齿轮系统;裂纹故障;啮合刚度;边频谱线;正交小波包;倒频谱

随着工业领域中生产技术的进步和自动化程度的提高，针对设备的在线监测和故障诊断技术正在受到更多的重视。齿轮传动系统作为机械设备中重要的运动和动力传递部件在高速和重载等恶劣的工作环境中容易发生故障而影响到设备的可靠运行，安全生产和经济效益[1]。因此，针对齿轮传动装置的设备监测和故障诊断技术的发展和应用也显得越来越重要。在实际的振动监测过程中齿轮的故障特征信号多具有信号微弱，噪声干扰强，故障种类复杂和不易识别等特点，目前针对齿轮传动装置的故障诊断技术还不够成熟，有待进一步研究和完善。

针对齿轮故障的研究，国内外学者分别从齿轮的动力学机理研究和信号特征提取等方面做了大量的工作。Wu等[2]基于齿轮系统的6自由度动力学模型分析了齿轮刚度随裂纹扩展的变化趋势。Ding等[3]研究了齿轮磨损故障的动力学行为。马锐等[4]建立了单级齿轮的扭转动力学模型，对齿轮在含裂纹情况下的非线性动力学特性进行研究。Mohammed等[5]使用短时傅里叶变换方法对齿轮裂纹故障进行了特诊提取。万志国等[6]提出了齿轮啮合刚度的一种修正计算方法，并采用小波方法对含裂纹故障的齿轮振动信号进行特征提取。李云等[7]提出一种基于包络角域同步平均的齿轮故障诊断方法。

本文在总结前人研究成果的基础上结合动力学仿真和故障特征分析方法开展齿根裂纹故障的研究。首先通过动力学的方法揭示仿真信号的边频特征，然后采用正交小波包和倒频谱相结合的方法对齿轮裂纹故障特征进行分析。

1 齿轮的啮合刚度计算

1.1 正常齿轮的啮合刚度计算

根据材料力学方法可将轮齿简化为变截面的悬臂梁(见图1)，此时啮合轮齿的综合弹性刚度由悬臂梁的弯曲刚度kb，剪切刚度ks和径向压缩刚度kc三部分组成，对应的公式表达如下

图1 轮齿受力示意图

(1)

(2)

(3)

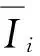
(4)

(5)

(6)

Ai=2Whi

(7)

(8)

式中:E为弹性模量;W为齿宽；Hp为节圆齿厚;v为泊松比。

实际轮齿的根部是弹性的轮缘，因此需要考虑齿轮基体的柔性变形，齿轮基体柔性变形所对应的刚度可表示为

(9)

式中,各参数详见文献[8]。

轮齿啮合中的赫兹刚度表示为

(10)

综上所述，一对齿轮副总的啮合刚度可表示为

(11)

1.2 含裂纹齿轮的啮合刚度计算

图2为轮齿裂纹的扩展模型，图2中裂纹存在于齿根处，假设裂纹和齿轮中心线的夹角为αc，裂纹深度为q。

图2 裂纹的扩展模型

当齿根产生裂纹时，轮齿的受力区域将发生变化，刚度计算中的截面模量Ii别和截面面积Ai将变为

(12)

(13)

将式(12)和式(13)代入齿轮刚度计算公式中可得到对应的含裂纹情况下的轮齿啮合刚度。齿轮参数如表1所示，假设在从动轮的齿根处产生裂纹，刚度计算结果如图3所示，图中分别包含了正常齿轮，裂纹深度为1 mm和裂纹深度为2 mm的啮合刚度曲线。

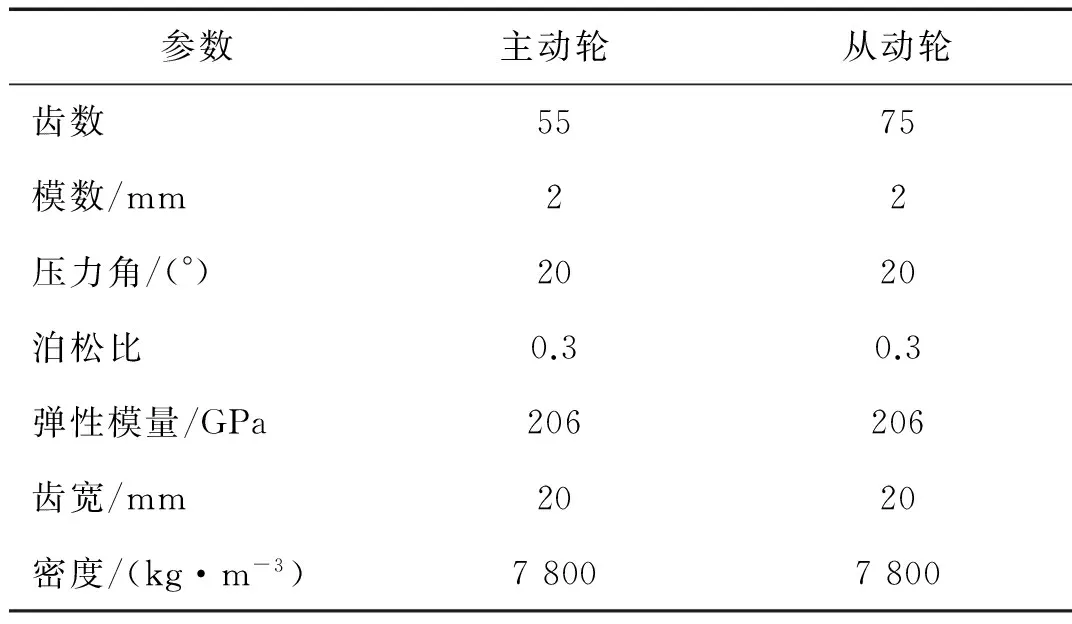
表1 齿轮参数

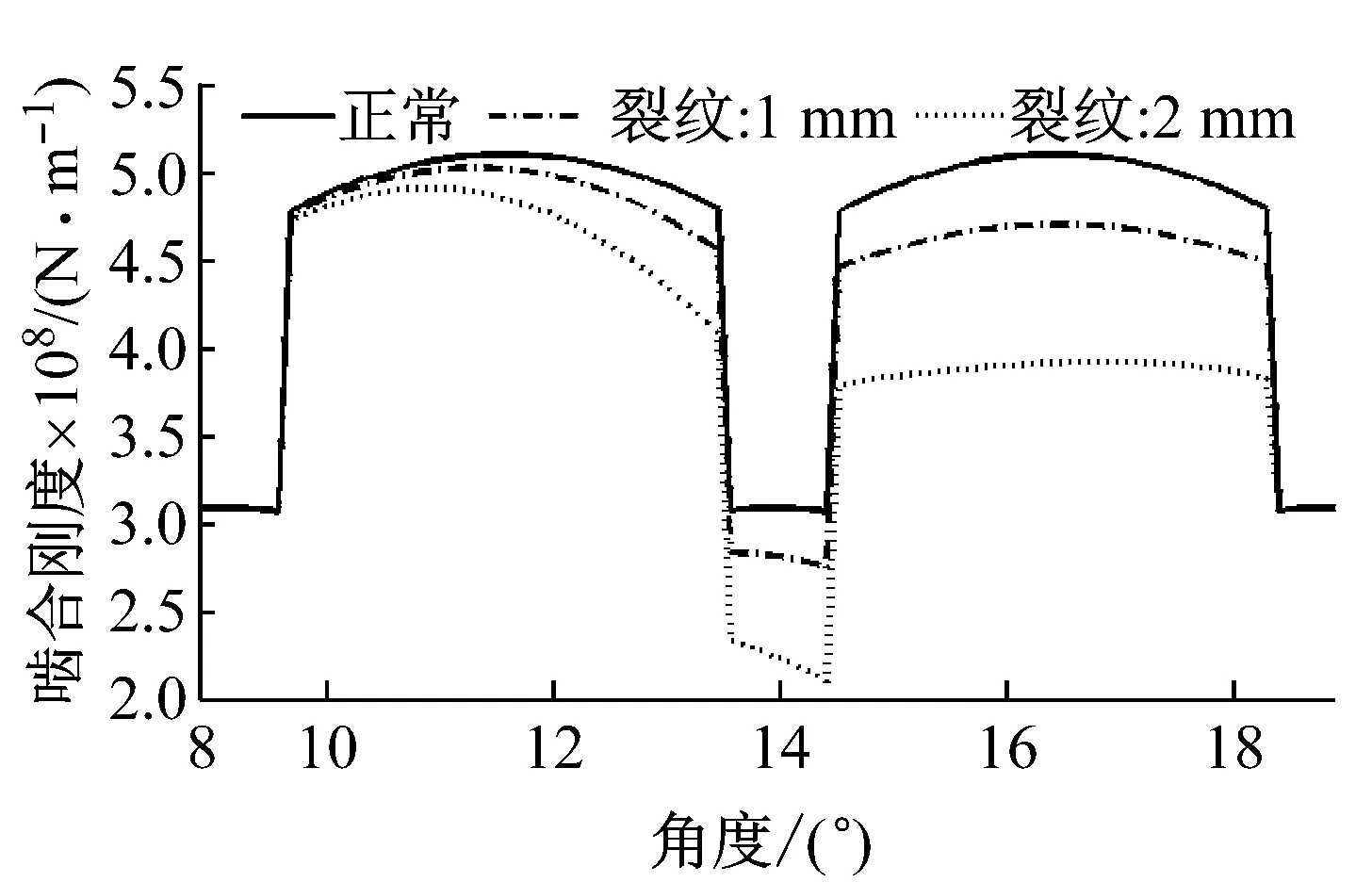
图3 啮合刚度曲线

为进一步揭示啮合刚度的频域特征，本文拟对刚度曲线进行阶次谱分析。值得强调的是，在转速恒定且未知的情况下，采用阶次谱比频谱更为方便，阶次谱不需要考虑时间信息，而得到的谱线结构与频谱一致，只是横坐标的表示有所区别。如图4所示，图4(a)为正常齿轮啮合刚度曲线对应的阶次谱，齿轮的1阶代表转频，图4中的谱线成分包括75阶(代表齿轮的啮合频率)及其倍阶次成分；图4(b)为齿根裂纹为2 mm时对应啮合刚度曲线的阶次谱，对比两图可以发现，齿根产生裂纹时会在低阶部分出现一系列间隔为1阶的谱线，这些谱线占据的谱带较宽，说明其在对应的频谱中的频带也较宽。这些低频谱线在动力学响应中与啮合频率及其倍频成分形成频率耦合而出现一系列的组合频率，这些组合频率围绕在啮合频率及其倍频附近，构成其边频成分。具体内容将在第3节(动力学仿真)作进一步说明。

2 齿轮系统动力学模型

根据考虑的因素的不同，齿轮动力学模型的建立包括多种方法，为了精确的描述齿轮系统的动态行为，本文考虑了轴承的支撑刚度，建立齿轮传动系统的6自由度动力学模型，如图5所示。图5中，Gear 1和Gear 2分别代表主动齿轮和从动齿轮。

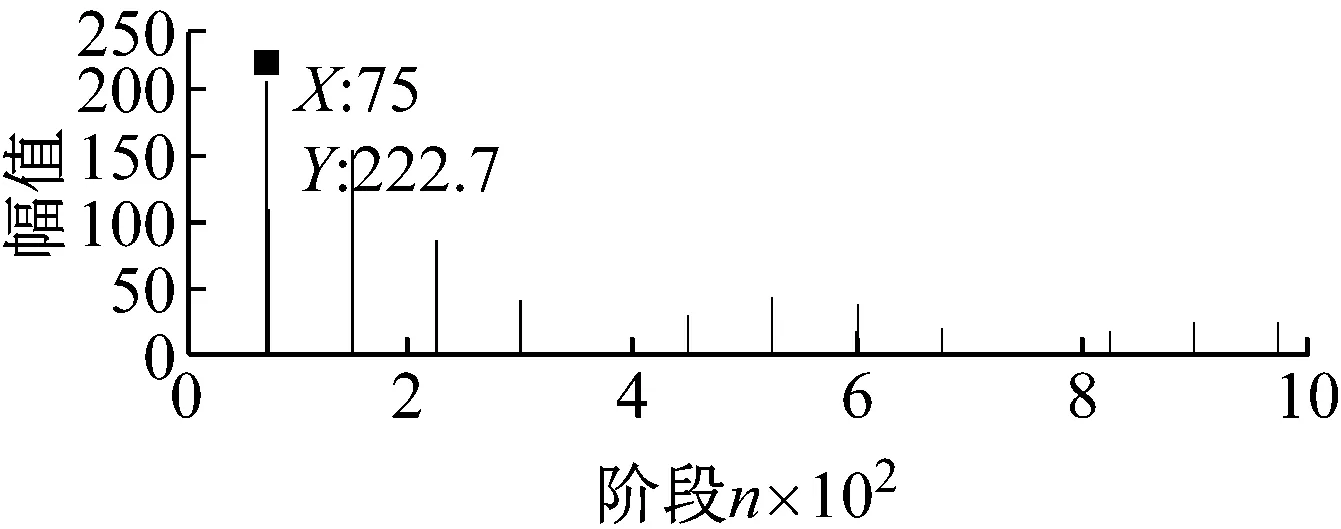
(a) 正常齿轮啮合阶次谱

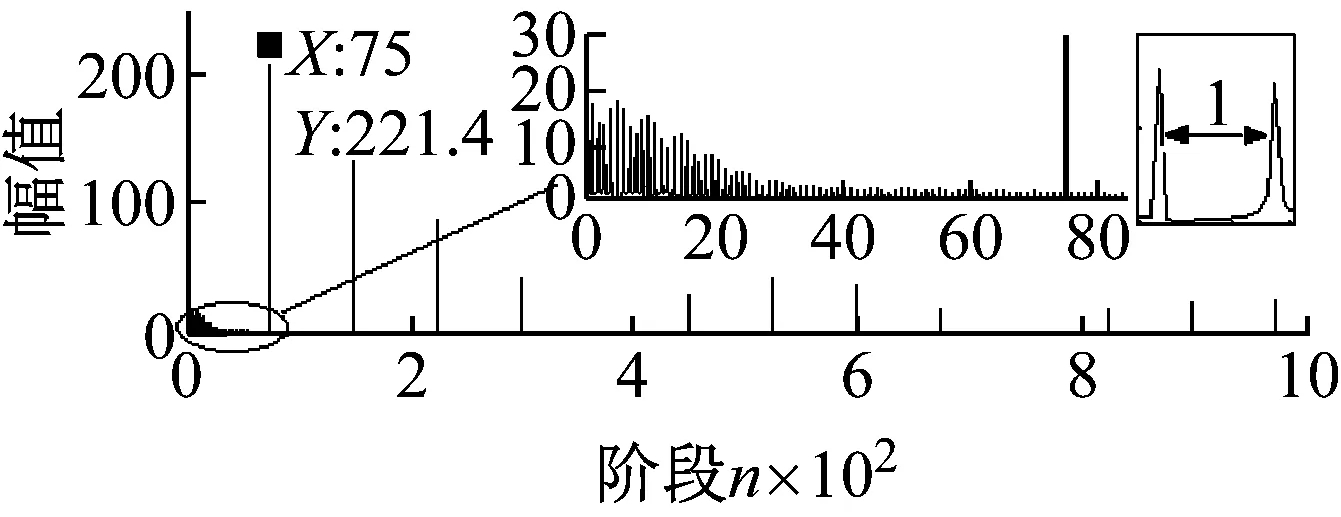
(b) 齿根裂纹2 mm的啮合阶次谱

图5 齿轮6自由度动力学模型

根据牛顿力学的方法建立方程组如下

(14)

其中，

式中:p12(t)为主动轮相对于从动轮在轮齿接触点公法线方向上的相对位移；m1、m2为主动轮和从动轮的质量；r1、r2为主动轮和被动轮的基圆半径；J1、J2为主动轮和被动轮的转动惯量；k12(t) 、c12(t)为齿轮的啮合刚度和阻尼；k1bx、k1by、k2bx、k2by和c1bx、c1by、c2bx、c2by分别为主动轮和从动轮的轴承刚度和阻尼；e12(t)为齿轮副的啮合误差，其公式为

e12(t)=Afcos(wft+φf)

(15)

式中，wf为动轮的啮合频率。

方程组中存在刚体位移，消除刚体位移后方程组可表示为

(16)

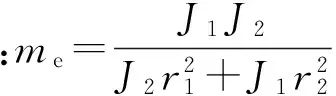
3 动力学仿真

相较于正常齿轮，轮齿裂纹的存在会导致齿轮系统在运动过程中产生周期性的冲击响应。在齿轮传动过程中，当含有齿根裂纹的轮齿参与啮合时，其啮合刚度减小，对应的刚度激励改变，进而引起系统的冲击响应。这种冲击具有周期性，冲击频率为从动轮的转频。由于裂纹的存在，齿轮啮合刚度的频谱会在低频处形成一系列等间隔的谱线，这些谱线占据的频带较宽(如图4所示)，在齿轮系统的动态响应中这些低频成分会与齿轮的啮合频率及其倍频成分等进行频率耦合而形成组合频率，在图谱上表现为齿轮的啮合频率及其倍频等附近的边频成分，对应的边频范围较宽，边频间隔等于从动轮的转频。

(a) 时域波形

(b) 幅值谱

Fig.6 Time domain waveforms and amplitude spectrum(normal)

正常齿轮的频谱主要包含啮合频率及其倍频信息，其基频为1 125 Hz，等于齿轮的啮合频率,如图6所示。而在图7～图8中还出现了明显的边频带，边频的间隔为15 Hz，等于从动轮的转频。随着裂纹的扩展，时域信号的冲击会不断增强，相较于图7，图8中的时域波形的冲击明显增强，边频幅值明显增大，从幅值谱图的放大显示(见图8(c))可以看到，当齿根裂纹为1 mm时，频谱中出现的边频幅值最高为0.21，而齿根裂纹为2 mm时，频谱中出现的边频幅值最高为0.52，边频成分明显增强。在实际的齿轮故障诊断中，当齿轮产生齿根裂纹时，其振动信号会在时域波形中出现周期性的冲击，冲击频率为裂纹齿轮所在轴的转频，对应的频谱在其啮合频率及倍频等位置附近出现边频带，边频间隔等于冲击频率。对比试验分析结果可知，该仿真信号符合齿轮箱故障诊断中实测信号的规律，验证了该仿真模型的可靠性，同时能够为工程实际信号的边频现象提供一种基于动力学原理的解释。

这些由齿根裂纹故障所形成的边频成分具有幅值较低，能量分散且分布不均匀的特点，在不同频带的幅值大小存在差异，如图7(c)和图8(c)所示。在啮合频率的基频或不同倍频附近出现的边频谱线的幅值具有明显的差异，其中在啮合频率的5倍频附近的边频幅值最高。在实际的测试中，振动信号包含有复杂的噪声，由裂纹故障引起的边频分量往往会被噪声信息淹没而难以分析。因此，针对边频能量在不同频带分布不均匀的特点，可以通过带通滤波将频带分解为多个子频段，然后对每个子频段进行分析。该方法一方面可以有效滤除宽频噪声的干扰，另一方面能够筛选出边频幅值较高的频段，突出边频信息，提高信噪比，能够更为有效的发现和提取信号的边频特征。

(a) 时域波形

(b) 幅值谱

(c) 幅值谱放大图

Fig.7 The time domain waveforms and amplitude spectrums(with crack fault:1 mm)

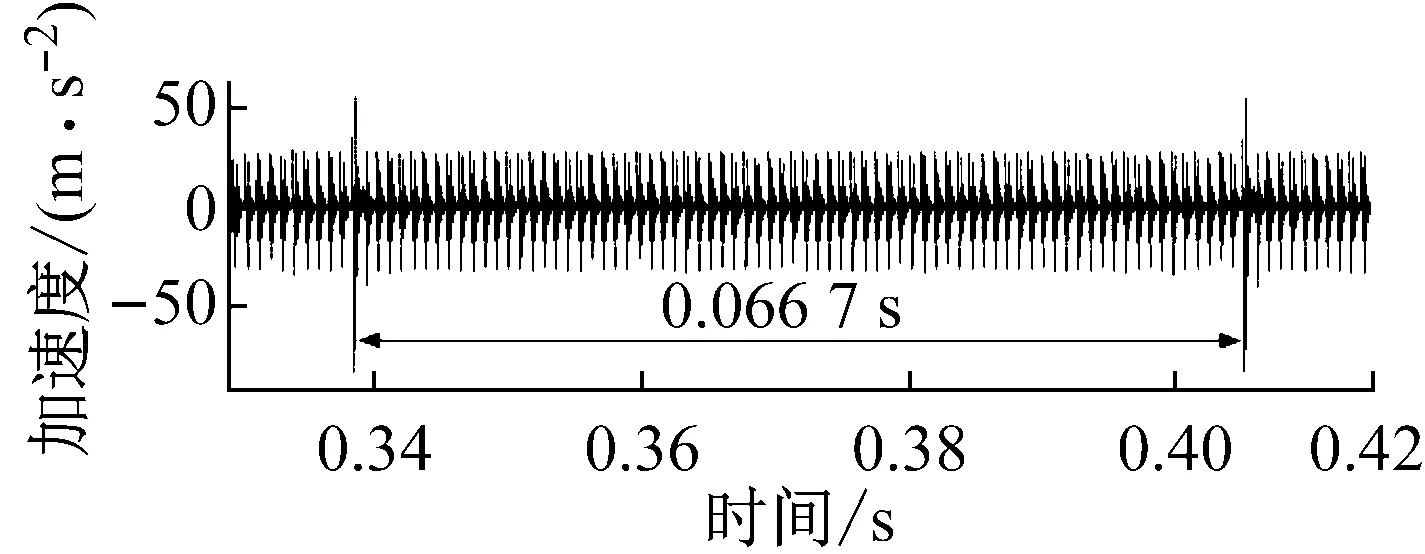
(a) 时域波形

(b) 幅值谱

(c) 幅值谱放大图

Fig.8 The time domain waveforms and amplitude spectrums(with crack fault:2 mm)

4 故障特征分析

根据上节对信号特征的分析，本节采用正交小波包与倒频谱相结合的方法来对信号的边频谱线进行分析与讨论。正交小波包能够为信号提供更加精细的分析方法，可以同时对信号的低频和高频进行多级分解，这种分解既无冗余，也无疏漏，便于实现信号的时频局部化分析[9]。而且，分解后的子频带有效消除了齿轮啮合频率及其倍频成分的干扰，便于利用倒频谱对边频成分进行分析。正交小波包分解过程可以形象的表示为一个二进制树结构图，如图9所示为小波包的3层分解过程。

在Daubechies小波系中滤波器长度系数为5的“db5”小波对突变信号比较灵敏且阶数比较低，本文选用“db5”小波函数作小波包分解，并选取小波包的第3层分解结果进行讨论。图9中(0,0)表示原始信号，dij表示在节点(i,j)处的小波包系数。对小波包进行重构后，用sij表示dij的重构信号，则小波包第3层分解重构后的信号依次为s30～s37，表2表示了这8个信号所代表的原信号的频率范围，表中fc代表原信号的截止频率。

图9 二进制树结构图

表2 8个信号所代表的原信号的频率范围

Tab.2 The frequency range represented by the 8 signals

信号频带范围信号频带范围s30[0,fc/8]s34[7fc/8,fc]s31[fc/8,2fc/8]s35[6fc/8,7fc/8]s32[3fc/8,4fc/8]s36[4fc/8,5fc/8]s33[2fc/8,3fc/8]s37[5fc/8,6fc/8]

图10～图11为s30～s37信号的时域波形，在进行分析时将分别对各个信号单独进行分析，以便于更为有效的分析边频成分。

通过正交小波包方法将信号分解为多个子频段的信号后，可以对各个信号单独进行分析，针对信号在啮合频率及其倍频等地方出现的边频谱线具有数量较多，幅值较小，而且具有明显的周期性，适宜采用倒频谱进行故障特征的提取，倒频谱分析方法能将图谱上同一系列的边频谱线简化为倒频谱上的单根或几根谱线，谱线的位置是原谱图上边频的频率间隔的倒数，谱线的高度反应了这一系列边频成分的强度[10]。

(a) s30信号

(b) s31信号

(c) s32信号

(d) s33信号

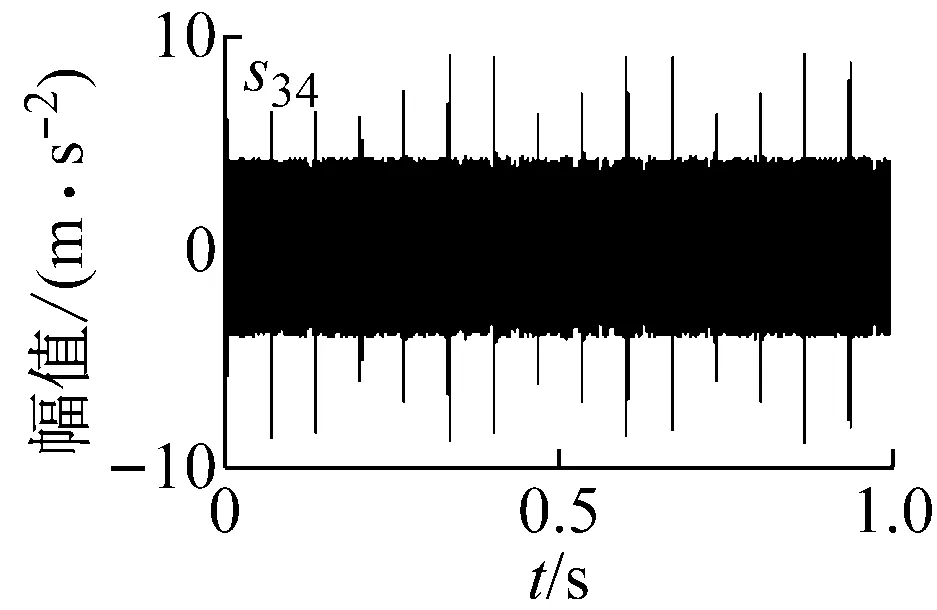
(a) s34信号

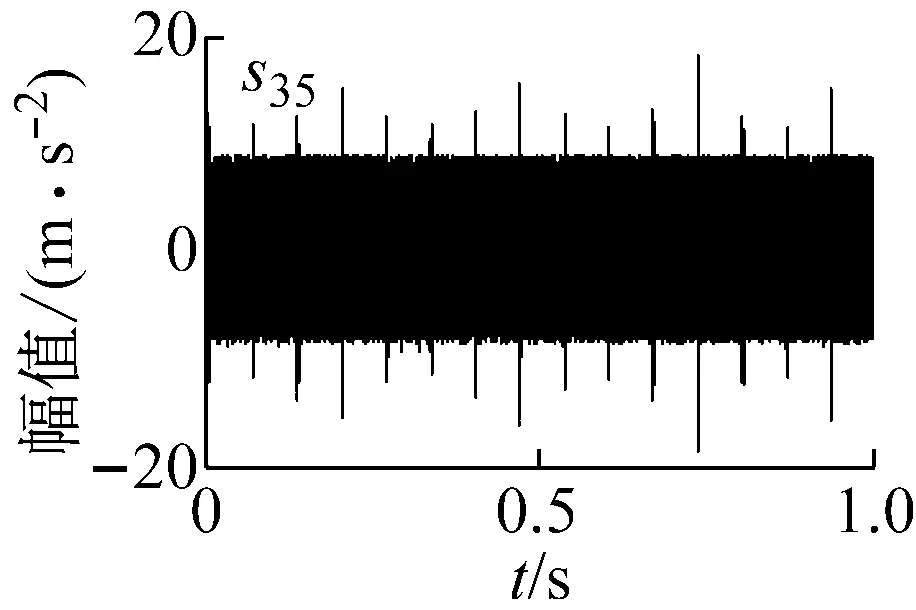
(b) s35信号

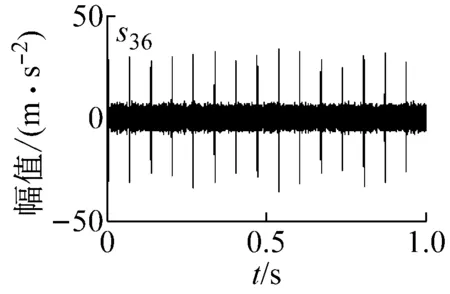
(c) s36信号

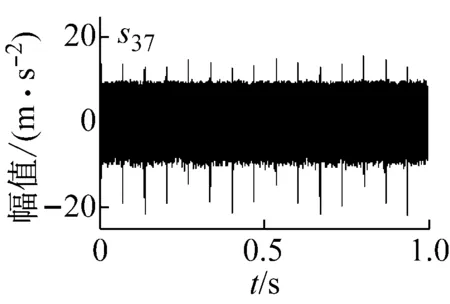
(d) s37信号

图12～图13为s30～s37信号对应的倒频谱，图谱中主要谱线的间隔在0.066～0.067，对应的频率近似为15 Hz，等于从动轮的转频。各个倒频率对应的幅值大小不同，其中s36中的倒频率幅值最高，第一条谱线的值约为0.115 8，反映出的信号的边频特征最为明显。

5 结 论

本文通过材料力学的方法计算含裂纹齿轮的啮合刚度，将其代入齿轮系统的动力学方程组中求解系统的动态响应，从时域中可以发现波形中存在周期性的冲击成分，在频谱啮合频率的基频及其倍频等地方形成一系列等间隔的边频谱线，其间隔大小等于故障齿轮的转频。这些边频成分幅值较低，能量分散且分布不均匀，而且在不同频带的幅值大小存在差异。在实际的测试中，振动信号包含有复杂的噪声，由裂纹故障引起的边频分量往往会被噪声信息淹没而难以分析。基于上述特征，本文首先通过正交小波包方法对信号的频带进行分解，然后将获得的各个子频带信号应用倒频谱进行分析，提取信号的边频成分。结果表明，采用正交小波包与倒频谱相结合的方法更加有助于发现和提取信号中由裂纹故障引起的边频成分。

(a) s30信号

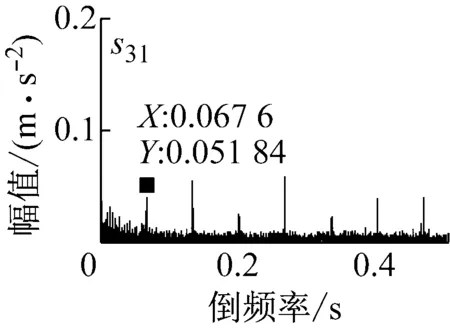
(b) s31信号

(c) s32信号

(d) s33信号

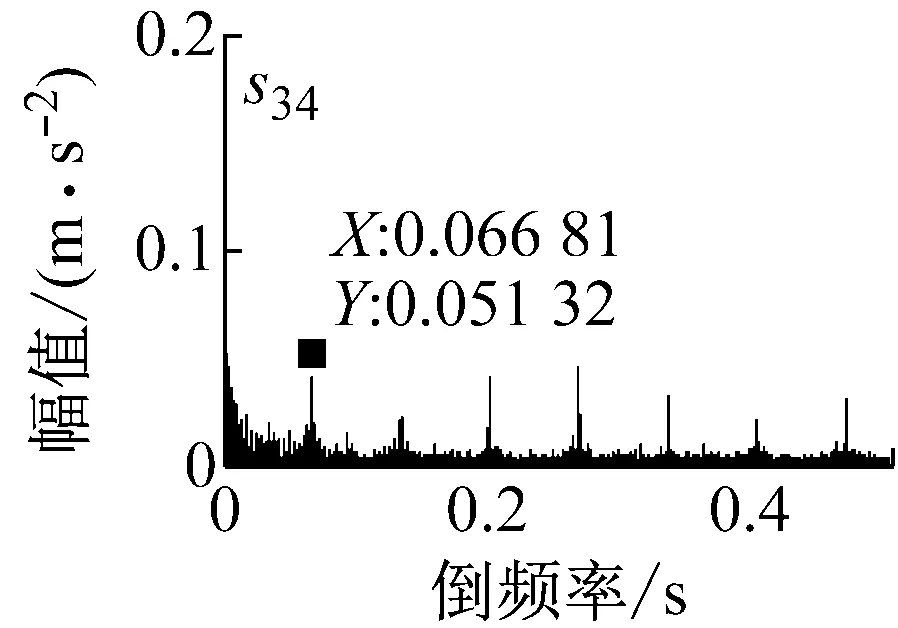
(a) s34信号

(b) s35信号

(c) s36信号

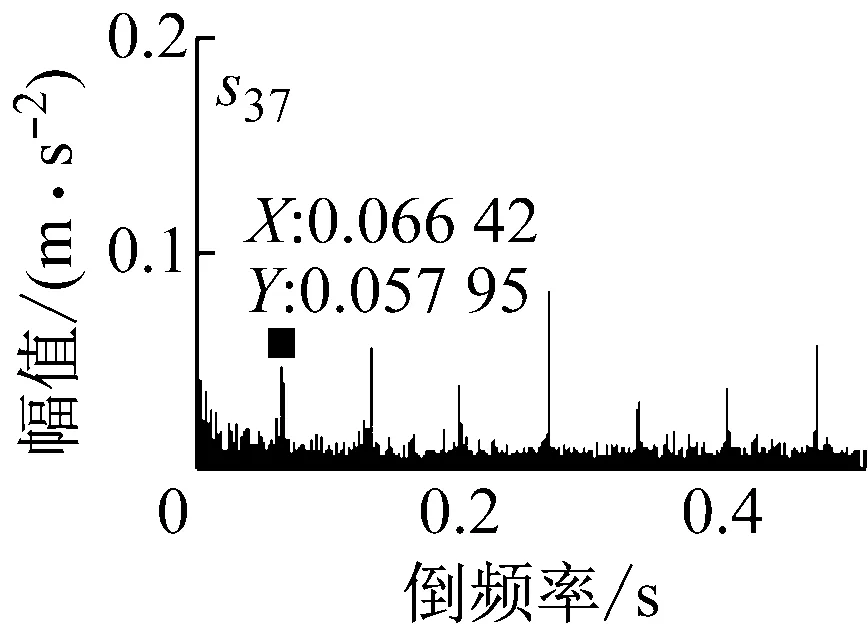
(d) s37信号

[1] 李润方, 王建军. 齿轮系统动力学—振动·冲击·噪声[M]. 北京: 科学出版社, 1997.

[2] WU Siyan, ZUO Mingjian, PAREY A. Simulation of spur gear dynamics and estimation of fault growth[J]. Journal of Sound and Vibration, 2008, 317(3): 608-624.

[3] DING H, KAHRAMAN A. Interaction between nonlinear spur gear dynamic and surface wear[J]. Journal of Sound and Vibration, 2007, 307(3): 662-679.

[4] 马锐, 陈予恕. 含裂纹故障齿轮系统的非线性动力学研究[J]. 机械工程学报, 2011, 47(21): 84-90.

MA Rui, CHEN Yushu. Nonlinear dynamic research on gear system with cracked failure[J]. Journal of Mechanical Engineering, 2011, 47(21): 84-90.

[5] MOHAMMED O D, RANTATALO M. Dynamic response and time-frequency analysis for gear tooth crack detection[J]. Mechanical Systems and Signal Processing, 2016, 66-67: 612-624.

[6] 万志国, 訾艳阳,曹宏瑞,等. 时变啮合刚度算法修正与齿根裂纹动力学建模[J]. 机械工程学报, 2013, 49(11): 153-160.

WAN Zhiguo, ZI Yanyang, CAO Hongrui, et al. Time-varying mesh stiffness algorithm correction and tooth crack dynamic modeling[J]. Journal of Mechanical Engineering, 2013, 49(11): 153-160.

[7] 李云, 郭瑜, 那靖,等. 基于包络同步平均的齿轮故障诊断[J]. 振动与冲击, 2013, 32(19): 17-62.

LI Yun, GUO Yu, NA Jing, et al. Gear fault diagnosis based on envelope synchronous average[J]. Journal of Vibration and Shock, 2013, 32(19): 17-62.

[8] CHAARI F, FAKHFAKH T, HADDAR M. Analytical modeling of spur gear tooth crack and influence on gear mesh stiffness[J]. European Journal of Mechanics A/Solids, 2009, 28(3): 461-468.

[9] 胡广书. 现代信号处理教程[M]. 北京: 清华大学出版社, 2004.

[10] 杨国安. 齿轮故障诊断实用技术[M]. 北京: 中国石化出版社, 2012.

Dynamic characteristics of a gear system with crack fault and its fault feature analysis

WANG Xu1, WU Xing1, XIAO Zhengming1, CAO Yongli2, LIU Tao1

(1. Faculty of Mechanical and Electrical Engineering, Kunming University of Science and Technology, Kunming 650500, China; 2. Kunming Yunnei Power Co., Ltd., Kunming 650500, China)

A multi-DOF mechanical model of a gear system with crack fault was established to study its failure mechanism based on the dynamic method, considering effects of time-varying mesh stiffness, transmission error and bearing support stiffness. First of all, meshing stiffnesses of gears in two cases including normal condition and the one with crack fault were calculated for the accurate dynamic characteristics analysis. The results of the system’s dynamic responses solved with the built dynamical model showed that there are some periodic impulses in time domain waveform, and there are some side frequencies equally spaced near the mesh fundamental frequency and its harmonic components, the interval between two side-frequencies is equal to the rotating frequency of the faulty gear; the amplitudes of side frequencies are lower and their energy is dispersive and not uniform, these amplitudes within different frequency bands are different. Aiming at the above mentioned features, the signal frequency band was decomposed with the orthogonal wavelet packet method and each sub-frequency band signal was analyzed using the cepstrum analysis method. The results showed that the proposed method can effectively improve the signal-to-noise ratio of signals, and make it easier to identify and extract side frequency components caused due to crack fault in signals to be detected.

gear system; crack fault; mesh stiffness; side frequencies; orthogonal wavelet packet； cepstrum

国家自然科学基金资助项目(51465021)；云南省教育厅科学研究基金重大专项项目(ZD2013004)；云南省自然科学基金(2013FB014)

2015-11-18 修改稿收到日期：2016-03-10

王旭 男，博士生，1987年生

伍星 男，博士，教授，博士生导师，1973年生

TH113

A

10.13465/j.cnki.jvs.2017.09.012