四列角接触球轴承振动特性研究

邓四二， 卢羽佳， 华显伟， 张言伟， 黄运生

(1.河南科技大学 机电工程学院，河南 洛阳 471003； 2.辽宁重大装备制造协同创新中心，辽宁 大连 116024)

四列角接触球轴承振动特性研究

邓四二1,2， 卢羽佳1， 华显伟1， 张言伟1， 黄运生1

(1.河南科技大学 机电工程学院，河南 洛阳 471003； 2.辽宁重大装备制造协同创新中心，辽宁 大连 116024)

基于滚动轴承动力学理论，建立了四列角接触球轴承的动力学分析模型，并以某型号四列角接触球轴承为例，对不同结构参数与工况参数下的轴承振动特性进行理论分析。结果表明：对于四列角接触球轴承，根据使用工况选择大、小球列不同的内、外沟曲率半径系数与初始接触角更有利于轴承的减振降噪；对轴承施加一定的轴向预紧量可有效减小轴承振动；存在较为合理的轴向载荷、倾覆力矩及内圈转速范围使四列角接触球轴承在使用时的振动较小。

四列角接触球轴承；动力学；结构参数；振动

传统的轮毂轴承单元多采用双列角接触球轴承与双列圆锥滚子轴承，新型的四列角接触球轴承作为轮毂轴承单元使用具有承载能力强、摩擦功耗小，制造成本低等优势，可以替代双列圆锥滚子轴承用于中型及重型汽车中[1]。作为轮毂轴承，四列角接触球轴承的振动特性将直接影响到汽车的安全性与舒适性。

轴承振动的产生机理非常复杂，涉及工艺误差、润滑剂、结构参数及工况参数等诸多因素[2]。解决轴承振动的基本方向为改善轴承的制造工艺，通过控制轴承在加工过程中产生的圆度、粗糙度及波纹度等误差实现轴承减振降噪的目的[3-7]。随着制造工艺的发展，当轴承精度超过某一界限时，轴承的振动水平不再由其制造精度决定，即使不存在几何误差，轴承仍会产生振动。目前有关轴承结构参数对轴承振动特性影响的研究主要集中于单列球轴承的钢球个数及径向游隙等：Aktürk等[8-9]分别建立了三自由度与二自由度的角接触球轴承支承的转子系统振动数学模型，对钢球数、预载荷与主轴的振动关系进行了研究；Bai等[10-11]分别建立了角接触球轴承与双列调心球轴承的动力学分析模型，开展了轴承径向游隙、径向力对轴承振动特性的影响研究；殷玉枫等[12-13]分别通过声学理论与滚动轴承动力学理论研究了深沟球轴承的沟曲率半径系数、径向游隙等结构参数对轴承振动噪声的影响。汽车轮毂轴承在工作时的受力情况比较复杂，四列角接触球轴承作为新型的汽车轮毂轴承单元结构，目前有关其振动特性理论的研究尚未见。鉴于此，本文基于滚动轴承动力学分析理论，建立了四列角接触球轴承的动力学分析模型，以某型号四列角接触球轴承为例，对轴承的工况和结构等参数与轴承振动特性的关系进行分析，研究结果可为四列角接触球轴承的设计提供一定的理论依据。

1 轴承动力学分析模型

四列角接触球轴承受载情况见图1，为便于对四列角接触球轴承进行动力学分析，作如下假设：轴承零件工作表面具有理想的几何形状，其形心与质心重合；轴承外圈固定，两内圈通过锁扣连结后以转速n绕X轴旋转；保持架由钢球引导；轴承承受径向载荷、轴向载荷及力矩载荷；坐标系{O;X,Y,Z}为轴承惯性坐标系。

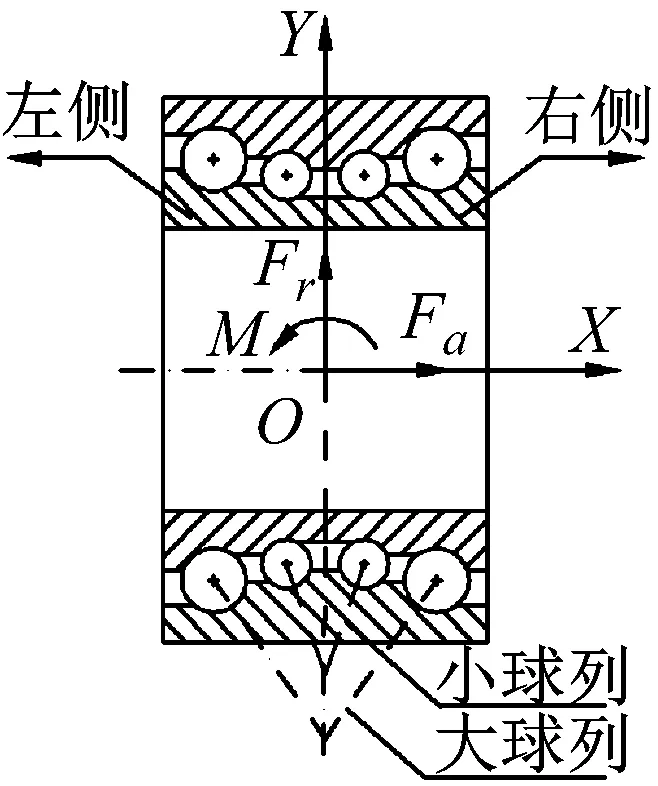
(a)

(b)

1.1 轴承各元件间相互作用力数学模型

图1中，设左侧大钢球所在的列为第1列、左侧小钢球所在的列为第2列、右侧小钢球所在的列为第3列、右侧大钢球所在的列为第4列，则第k列第j个钢球的受力情况见图2；位于第k列的保持架受力情况见图3；轴承内圈的受力情况见图4。图2～图4中相关符号的含义见表1，其值求解法参见文献[14]。

(a)左侧钢球x-y平面(b)左侧钢球y-z平面(c)左侧钢球x-z平面(d)右侧钢球x-y平面(e)右侧钢球y-z平面(f)右侧钢球x-z平面

图2 钢球受力示意图

Fig.2Schematicdiagramofballforces

1.2 轴承动力学微分方程

根据轴承各零件的受力情况可建立四列角接触球轴承各零件的动力学微分方程组。

表1 符号说明

图3 保持架受力示意图

图4 内圈受力示意图

钢球的动力学微分方程组为

(1)

(2)

(3)

(4)

(5)

(6)

保持架动力学微分方程组为

(7)

(8)

(9)

内圈动力学微分方程组为

(10)

(11)

(13)

(14)

2 轴承振动特性分析

采用GSTIFF(Gear Stiff)变步长积分算法对建立的四列角接触球轴承动力学微分方程式(1)～式(14)进行求解，以某型号四列角接触球轴承为例，对轴承的工况和结构等参数与轴承振动特性的关系进行分析。轴承主参数如表2所示，内、外圈及滚动体的材料为GCr15，保持架的材料为尼龙材料PA66。

表2 四列角接触球轴承结构参数

本文采用轴承振动加速度级法[15]得到的轴承运转分贝值来评价轴承的振动，分贝值定义为

DB=20lg(a/a0)

(15)

式中:a为某一频带范围内的轴承振动加速度均方根值；a0为参考加速度，a0=9.81×10-3m/s2。

2.1 结构参数对轴承振动的影响

设轴承在环境温度下工作，分析轴承在内圈转速为900 r/min，径向载荷为5 900 N，轴向载荷为2 400 N，力矩载荷为644.325 N·m，轴承轴向预紧量为10 mm时，不同结构参数对轴承振动特性的影响。

2.1.1 内沟曲率半径系数对轴承振动的影响

图5为四列角接触球轴承的大、小球列在不同初始接触角α下，轴承的内沟曲率半径系数对其振动的影响。由图5可知，对于轴承的大、小球列，随着内沟曲率半径系数以及初始接触角的增加，轴承振动均呈现先减小后增加的趋势，因此，对于给定工况条件，存在最优的内沟曲率半径系数与初始接触角，使四列角接触球轴承的振动最小。由图5还可知，轴承振动最小时，大、小球列对应的最优内沟曲率半径系数与最优初始接触角均不同，因此,在设计四列角接触球轴承时，可以考虑针对轴承大、小球列选择不同的内沟曲率半径系数与初始接触角，以最大限度的降低轴承振动。

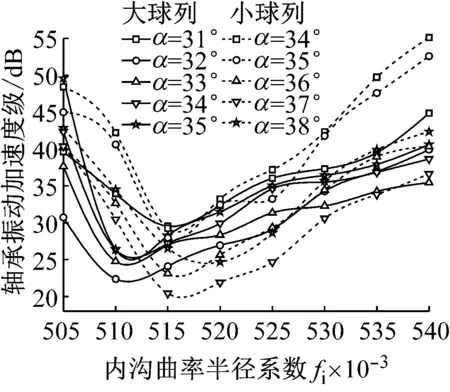
图5 内沟曲率半径系数对轴承振动的影响

Fig.5 Effect of inner groove curvature radius coefficients on vibration value

2.1.2 外沟曲率半径系数对轴承振动的影响

图6为四列角接触球轴承的大、小球列在不同初始接触角下，轴承的外沟曲率半径系数对其振动的影响。由图6可知，轴承振动随外沟曲率半径系数与初始接触角的增加呈先减小后增加的趋势，因此，对于轴承的大、小球列，均存在一个使轴承振动最小的外沟曲率半径系数与初始接触角。与内沟曲率半径系数类似，在给定工况下，大、小球列在轴承振动最小时对应的外沟曲率半径系数与初始接触角均不同，因此,在设计四列角接触球轴承时，可以考虑对轴承大、小球列选择不同的外沟曲率半径系数与初始接触角，以最大限度的降低轴承振动。

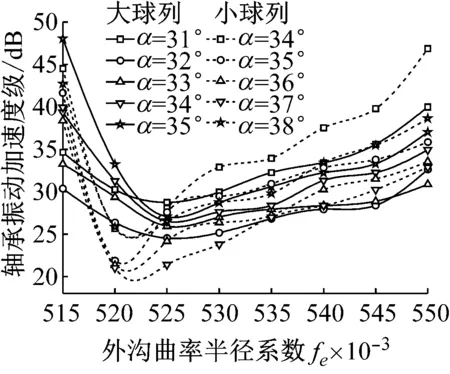
图6 外沟曲率半径系数对轴承振动的影响

2.1.3 保持架兜孔间隙对轴承振动的影响

图7为四列角接触球轴承在左、右两侧的两个保持架分别为整体式设计与分离式设计时，保持架兜孔间隙对轴承振动的影响。由图7可知，随着保持架兜孔间隙的增加，轴承振动呈先减小后增加的趋势，因此,存在最优的保持架兜孔间隙使轴承的振动最小。由图7还可知，对于保持架采用整体式设计的轴承，随着保持架兜孔间隙的变化，其振动值均大于保持架采用分离式设计的轴承，因此，分离式设计的保持架更有利于轴承的减振降噪。

图7 保持架兜孔间隙对轴承振动的影响

2.2 工况参数对轴承振动的影响

设轴承在环境温度下工作，分析轴承结构参数为初始设计值时，不同工况参数对轴承振动特性的影响。

2.2.1 径向载荷对轴承振动的影响

图8为四列角接触球轴承在内圈转速为900 r/min，轴向载荷为0 N，力矩载荷为0 N·m，轴承轴向预紧量δ分别为5 mm，10 mm，15 mm，20 mm时，轴承承受的径向载荷对轴承振动的影响。由图8可知，随着径向载荷的增加，轴承振动也逐渐增加；随着轴向预紧量的增加，轴承振动呈现先减小后增加的趋势，且在径向载荷较小时，轴承的最优轴向预紧量较小，径向载荷较大时，轴承的最优轴向预紧量也较大，因此，可以根据给定工况选择合理的轴承轴向预紧量，以最大限度的降低轴承振动。

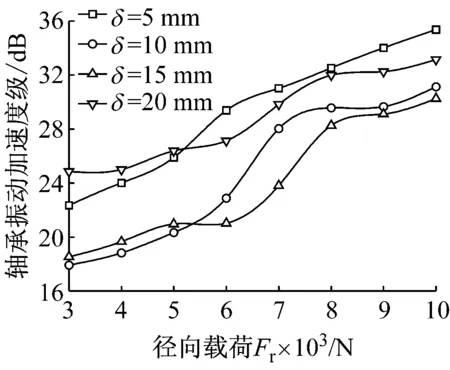
图8 径向载荷对轴承振动的影响

2.2.2 轴向载荷比对轴承振动的影响

图9为四列角接触球轴承在内圈转速为900 r/min，径向载荷为5 900 N，力矩载荷为0 N·m，轴承轴向预紧量为10 mm时，轴承轴向载荷比对轴承振动特性的影响。轴向载荷比Ca定义为轴承轴向载荷与径向载荷之比：Ca=Fa/Fr。由图9可知，随着轴向载荷比的增加，轴承振动呈先基本不变后逐渐增加的趋势。因此,对给定结构的轴承，存在一个合理的轴向载荷使用范围，使轴承运转过程中的振动较小。

图9 轴向载荷比对轴承振动的影响

2.2.3 倾覆力矩对轴承振动的影响

图10为四列角接触球轴承在内圈转速为900 r/min，径向载荷为5 900 N，轴向载荷为2 400 N，轴承轴向预紧量为10 mm时，轴承承受的倾覆力矩对轴承振动特性的影响。由图10可知，随着倾覆力矩的增加，轴承振动呈先缓慢增加后迅速增加的趋势。因此,对于给定结构的轴承，存在一个较为合理的倾覆力矩使用范围，使轴承在运转时的振动较小。

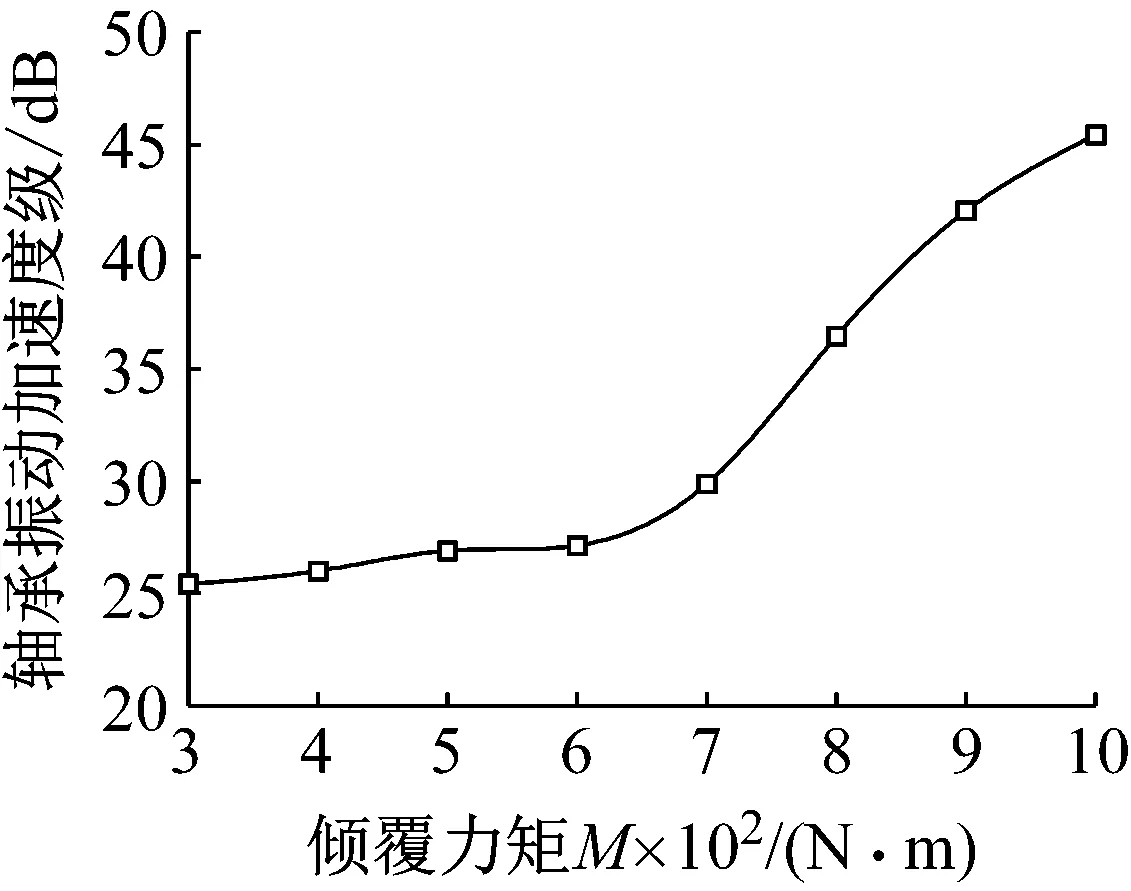
图10 倾覆力矩对轴承振动的影响

2.2.4 内圈转速对轴承振动的影响

图11为四列角接触球轴承在径向载荷为5 900 N，轴向载荷为2 400 N，轴承轴向预紧量为10 mm，倾覆力矩为644.325 N·m时，内圈转速对轴承振动特性的影响。由图11可知，随着内圈转速的增加，轴承振动呈先增加后减小而后继续增加的趋势，因此,对于给定结构的轴承，存在一个合理的转速使用范围。

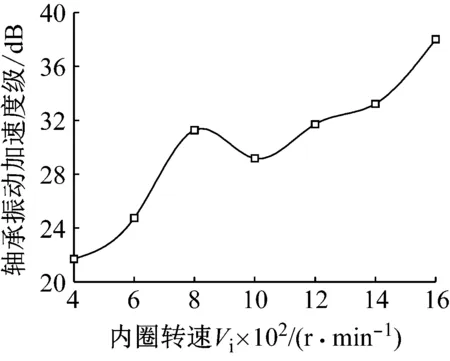
图11 内圈转速对轴承振动的影响

3 结 论

(1) 对于四列角接触球轴承，存在最优的内、外沟曲率半径系数与初始接触角使轴承的振动最小；根据工况参数选择轴承大、小球列不同的内、外沟曲率半径系数与初始接触角更有利于轴承的减振降噪。

(2) 对四列角接触球轴承施加一定的轴向预紧量可有效降低轴承的振动值，但过大的轴向预紧量会导致轴承振动迅速增大。

(3) 四列角接触球轴承在运转过程中，存在较为合理的轴向载荷、倾覆力矩及内圈转速使用范围使轴承的振动较小。

致谢：感谢辽宁重大装备制造协同创新中心支持。

[1] 谢夫勒两合公司. 角接触球轴承结构的车轮轴承单元[P]. 德国:80020034.1, 2006-12-20.

[2] 赵联春. 球轴承的振动研究[D]. 杭州：浙江大学，2003.

[3] AKTÜRK N. The effect of waviness on vibrations associated with ball bearings[J]. ASME Journal of Tribology, 1999, 121(4): 667-677.

[4] HARSHA S P, SANDEEP K, PRAKASH R. Nonlinear dynamic behaviors of rolling element bearings due to surface waviness[J]. Journal of Sound and Vibration, 2004, 272(3): 557-580.

[5] JANG G, JEONG S W. Vibration analysis of a rotating system due to the effect of ball bearing waviness[J]. Journal of Sound and Vibration, 2004, 269(3/4/5): 709-726.

[6] HARSHA S P. The effect of ball size variation on nonlinear vibration associated with ball bearings[J]．Journal of Multi-body Dynamics, 2004, 218(4):191-210．

[7] 顾晓辉，杨绍普，刘永强，等. 表面波纹度对滚动轴承—转子系统非线性振动的影响[J]. 振动与冲击，2014，33(8)：109-114.

GU Xiaohui, YANG Shaopu, LIU Yongqiang, et al. Effect of surface waveness on nonlinear virbtarion of a rotor with ball bearings[J]. Journal of Vibration and Shock, 2014, 33(8): 109-114.

[8] AKTÜRK N, UNEEB M, GOHAR R. The effects of number of balls and preload on vibrations associated with ball bearings[J]. Journal of Tribology, 1997, 119(4): 747-753.

[9] HARSHA S P, SANDEEP K, PRAKASH R. Effects of preload and number of balls on nonlinear dynamic behavior of ball bearing system[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2003, 4(3): 265-278.

[10] BAI Changqing, XU Qingyu. Dynamic model of ball bearings with internal clearance and waviness[J]. Journal of Sound and Vibration, 2006, 294(1):23-48．

[11] ZHUO Yaobin, ZHOU Xiaojun, YANG Chenlong. Dynamic analysis of double-row self-aligning ball bearings due to applied loads, internal clearance, surface waviness and number of balls[J]. Journal of Sound and Vibration, 2014, 333(23):6170-6189.

[12] 殷玉枫，张建水. 结构参数对轴承振动噪声的影响[J]. 噪声与振动控制，2014，34(1)：76-81.

YIN Yufeng, ZHANG Jianshui.Effect of structural parameters on vibration noise of rolling bearings[J]. Noise and Vibration Control, 2014, 34(1):76-81.

[13] 邓四二，孙朝阳，顾金芳，等. 低噪音深沟球轴承振动特性研究[J]. 振动与冲击，2015，34(10)：12-19.

DENG Sier, SUN Chaoyang, GU Jinfang, et al.Study on the vibration characteristics of low-noise deep groove ball beaings[J].Journal of Vibration and Shock, 2015, 34(10): 12-19.

[14] 邓四二，郝建军，滕弘飞，等. 角接触球轴承保持架动力学分析[J].轴承，2007(10)：1-5.

DENG Sier, HAO Jianjun, TENG Hongfei, et al. Dynamic analysis on cage of angular contact ball bearings[J]. Bearing, 2007(10): 1-5.

[15] 滚动轴承振动(加速度)测量方法:JB/T 5314—1991[S]. 北京：机械科学研究院，1991.

Vibration characteristics of four-column angular contact ball bearings

DENG Sier1,2, LU Yujia1, HUA Xianwei1, ZHANG Yanwei1, HUANG Yunsheng1

(1. School of Machatronics Engineering, Henan University of Science and Technology, Luoyang 471003, China;2. Collaborative Innovation Center of Major Machine Manufacturing of Liaoning, Dalian 116024, China)

Based on the dynamic theory of rolling bearings, the dynamic model of four-column angular contact ball bearings was established. Taking a certain type of four-column angular contact ball bearing as an example, the vibration characteristics of the bearing were investigated under different structural parameters and working conditions. The results showed that designing different inner and outer raceway groove curvature radius coefficients and different initial contact angles of different columns, respectively leads to lower vibration based on a specific working condition; a certain axial preload can reduce bearing vibration effectively; there are a reasonable axial load, an overturning moment and a rotating speed range to make the bearing vibration smaller.

four-column angular contact ball bearing; dynamics; structural parameters; vibration

河南省科技创新杰出人才(144200510020)；国家自然科学基金项目(U1404514)；广东省省级科技计划项目(2013B011301020)

2015-12-01 修改稿收到日期：2016-03-18

邓四二 男,博士,教授,博士生导师,1963年生

卢羽佳 女,硕士生,1991年生

TH133.33

A

10.13465/j.cnki.jvs.2017.09.001