数学师范生的SCK发展调查研究——以小学数学数与运算内容为例

王爱玲

（1．华东师范大学，上海 200241；2．菏泽学院，山东 菏泽 274015）

数学师范生的SCK发展调查研究
——以小学数学数与运算内容为例

王爱玲1，2

（1．华东师范大学，上海 200241；2．菏泽学院，山东 菏泽 274015）

以数学课程教学论课程为依托，以小学数学数与运算内容为例，对数学师范生的SCK的发展进行研究发现：数学课程教学论的教学能够有效促进数学师范生的SCK增长．但是数学师范生的SCK仍旧薄弱，有待提高，对影响数学师范生SCK的因素进行反思是十分必要的．

专门的学科知识（SCK）；数学课程教学论；数学师范生；专业成长

1 研究背景

PISA、TIMSS大型国际测试表明，中国中小学学生基础扎实，而创新实践能力不足，进一步表现为高等教育很难培养出一流的人才．张奠宙先生称此现象为“花岗岩上盖茅草房”．如何保持中国教育基础扎实，又能吸收国外的先进教育理念，培养基础稳健又有创新能力的人才是中国教育理念的努力方向．在新修订的课程标准中，将“双基”（基本知识、基本技能）扩展为“四基”（基本知识、基本技能、基本思想、基本活动经验），将“两能”（分析问题、解决问题）扩展为“四能”（发现问题、提出问题、分析问题、解决问题），这是教育理念的进步．而教师的知识能力能否适应这一要求是教育工作者关注的大事，这涉及到基础教育改革的成败．作为培养教师的主要母机——高等院校的师范专业肩负重任，如何培养出合格乃至优秀的基础教育教师意义重大．

教师职前培养是培养教师专业化发展进程中的一个重要阶段，也是提高国家师资质量的一个重要环节．师范教育是教师专业化发展的重要奠基阶段，提高数学师范生专门学科知识（SCK）对他们专业化发展有非常重要的作用，而数学课程教学论课程是高师培养中小学数学教师的必修课之一，因此选择以数学课程教学论课程为依托，研究数学师范生SCK的发展．

关于数学教学知识，近几年国内外学者更多研究了面向教学的数学知识（MKT）和学科教学知识（PCK）．国外学者Ball、Swars等有很多论文研究职前小学数学教师的MKT或PCK，国内学者庞雅丽研究了职前数学教师的MKT，徐章韬从历史发生的视角研究了数学师范生 PCK．中外学者对MKT或PCK的研究不断有新作品问世，有些研究也具体涉及到SCK．如学者陈曦对高中数学教师MKT的研究，测试分析了高中数学教师MKT的各个维度，包括SCK．但是学者们很少从SCK的视角去研究数学教师或职前数学教师的专业发展．

2 SC K的界定

学科教学知识（PCK）的想法开始作为一个模型出现，第一次被舒尔曼（Shulman，1986）描述[1]．舒尔曼设想了包括几类知识的教师知识理论框架．Ball and Bass（2000）利用术语面向教学的数学知识（MKT）来表示教师需要的专业数学知识，他们认为这些知识不同于其它领域需要的知识[2]．在 MKT模型不断进化中，Ball（2008）等提出了一个改进的舒尔曼分类（见图1）[3～4]．

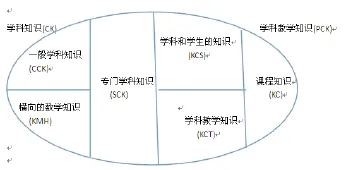
图1 面向教学的数学知识（MKT）的纬度

他们将面向教学的数学知识（MKT）分为两大类：学科知识（CK）和学科教学知识（PCK）．CK又有3个维度：一般学科知识（Common Content Knowledge，简称CCK），专门学科知识（Specialized Content Knowledge，简称SCK），横向数学知识（Knowledge at Mathematical Horizon，简称KMH）．PCK的 3个维度包括：学科与学生的知识（Knowledge of Content and Students，简称KCS），学科与教学的知识（Knowledge of Content and Teaching，简称KCT），课程知识（Knowledge of Curriculum，简称KC）．其中SCK是指在教学实践中教师经常使用的数学知识，但又高于课程知识，包括：能意识到问题的所有可能解决方法；对学生的回答能准确判断是否正确；有辨别和分析学生错误的能力；知道哪些解答可进行推广[5]．

近年来，还有一些研究者（Hill等）提出了专门学科知识（SCK），他们认为SCK不同于Shulman’s（1986）的学科主题知识（SMK）和学科教学知识（PCK）．SCK被定义为“对学生完成经常发生的数学教学任务需要的数学知识”．具体来说，Hill解释，SCK由“数学任务组成，比如，用图片或教具操作表示数和运算，从非标准解决方法中检验和推广，为数学思想或过程提供解释”[6]．SCK是一种数学学科知识，它不依赖学生的知识，也不依赖教学知识[7]．

综合上述理解，对 SCK界定为：Specialised Content Knowledge（SCK）是为了教学教师必须具备的更为专门化的一类数学学科知识，这类知识比学生所学的数学知识处于较高一级的水平．要求教师懂得问题的各种各样的解决方法，能够分析学生错误的原因和本质，解释常规、非常规算法和程序．

3 研究方法

主要采用问卷调查法和访谈法．

3.1 取 样

选取H大学数学系数学与应用数学专业（本科）、数学教育专业（专科）的部分学生作为研究对象．

H大学数学系开设数学课程教学论（一）和数学课程教学论（二）．每周4节课，每节课50分钟，要求两个学期完成教学任务．专科与本科由研究者授课，教学内容大致类似，研究者授课时根据具体情况做了适当的调整．数学课程教学论（一）侧重于数学教育理论, 数学课程教学论（二）侧重于初等数学内容方法．

3.2 工 具

学习教数学（LMT）工具用来测量教师的专门数学学科知识．该工具反应了Deborah Ball和她的同事在密西根大学的工作，由多个任务构成[8]．关于数与运算的测试项目14个，研究者检验了该工具的信度和效度[9]．课题研究者对上述14个任务进行了简单的改编，主要是跟据本土实情，特别是针对文化背景，进行了适当改编，也包括对简单数字的改编．H大学的数学教育研究小组认为改编后的项目不违背原设计者的意图．改编后的这14个项目作为测试工具．

3.3 研究过程

在新学期的第一个星期，研究者向自己授课班级的学生发布进行问卷调查的信息．在辅导员老师的协助下，在2015年9月新学期的第一个星期天的晚自习，两个专业的被试者将配合研究者完成对问卷的前测．

后测是在2016年6月底（第二个学期末）完成，也就是刚刚结束数学课程教学论（二）的学习，由先前的志愿者参与完成试卷的问答．

在后测结束后对学生进行访谈．

收集数据和访谈在学生学习数学课程教学论（一）和数学课程教学论（二）的一学年内完成．

4 数据分析的结果

4.1 参与研究的师范生信息

参与前测的学生有133人，实验过程中有3人退出，只有130名同学参与了后测，剔除无效问卷1份，有效问卷129份．参与测试的这129名师范生，包括两个专业，由于师范专业特色，女生居多，详见表1．

表1 参与研究的人口信息

4.2 数学师范生的SCK发展变化分析

问卷包括14个问题，每个问题1分，共14分．

下面是每个小题做对的人数及在专业人数中所占的百分比，详见表2～4．

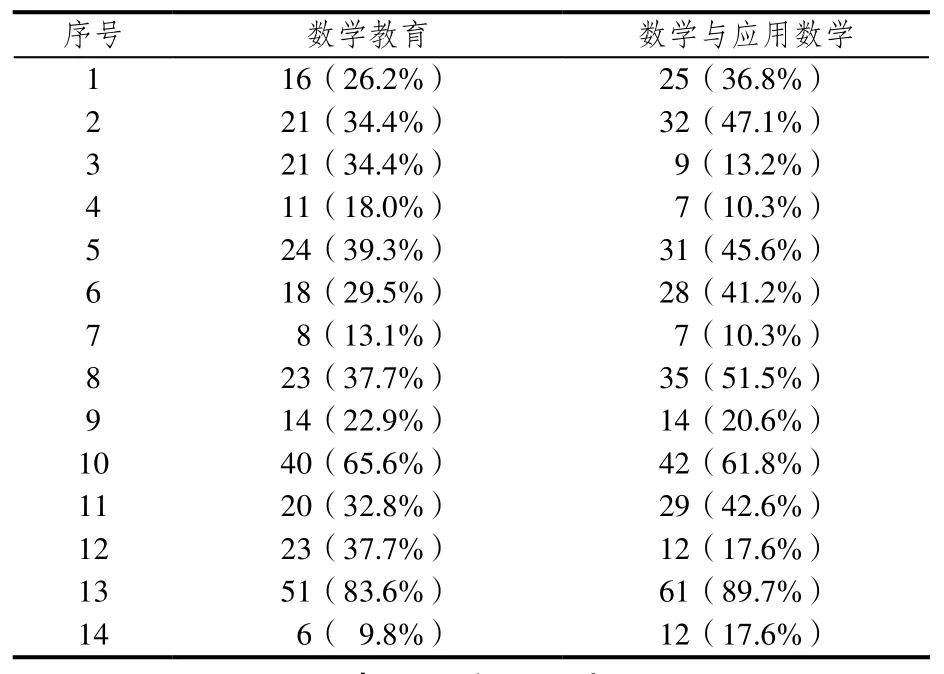
表2 前 测

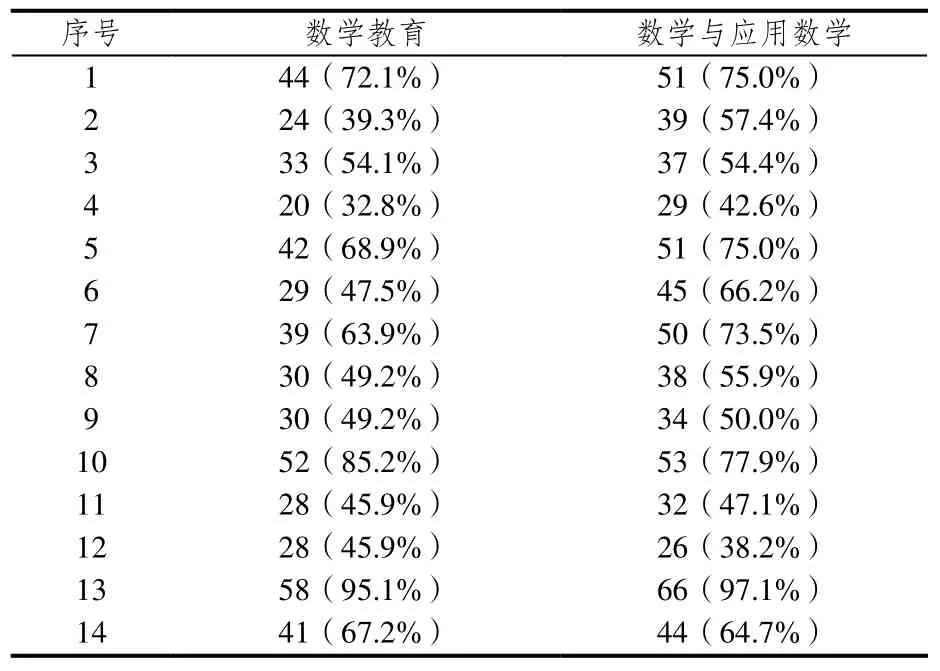
表3 后 测

表4 前测后测平均分数分布表

由表2，表3和表4可以看出，数学与应用数学专业和数学教育专业的学生在一学年的数学课程教学论学习中SCK都有了显著增长．

表2和表3反应了问卷中每个问题在后测中回答正确的人数比前测中都有增加，后测中每一个问题回答正确人数所占的百分比较前测有不同程度的提高．在前测中，两个专业每小题做对的人数几乎没有过半的，后测中情况仍不容乐观．比如数学教育专业的学生第十四题做的最差，61人中只有6人做对，占总人数的9.8%，后测中有41人选对，占本专业人数的67.2%．前测中数学与应用数学专业的学生第四题和第七题表现最差，68人中都只有7人做对，各占总人数的10.3%，后测中第四题有49人选对，占本专业总人数的 42.6%，后测中第七题本专业的学生进步较大，有 50人做对，占该专业总人数的73.5%．

由表 4可以看出两个专业的学生后测平均成绩明显好于前测平均成绩．数学教育专业的学生前测平均得分 4.86分，后测平均得分8.16分，前后平均增加了3.3分；数学与应用数学专业的学生前测平均得分 5.1分，后测平均得分8.75分，前后平均增加了3.65分．问卷总分是14分，从学生的平均得分来看，参与测试学生的SCK是薄弱的，虽然经过数学课程教学论的学习，学生的SCK有了显著增加，但仍不够理想．后测中数学教育专业学生的平均分是 8.16分，数学与应用数学专业的学生平均分是8.75分，距离14分的差距还很大．如何提高数学师范生的SCK仍是困扰研究者的问题．

数学与应用数学专业的学生是本科生，数学教育专业的学生是专科生，数学与应用数学专业的学生入校成绩高于数学教育专业的学生．无论前测还是后测，数学与应用数学专业的学生成绩都优于数学教育专业的学生，数学与应用数学专业的学生前测后测平均成绩变化也比数学教育专业的学生大一些，这里存在着基础问题，也说明了学生基础越好学习能力也较强，SCK也提高快一些．但是数学与应用数学专业的学生优势也不是那么明显，他们前测、后测的平均成绩分别稍高于数学教育专业的学生，两个专业前测后测平均成绩增长的幅度也没有太大的差异．

5 访 谈

5.1 情况简介

从参与测试的师范生中召集了一些志愿者参与访谈，报名的有14名同学，在后测结束后从14名同学中随机抽取了4名同学参与访谈．其中数学与应用数学专业、数学教育专业各有两名同学参与了访谈，在第二次测试不久对他们进行了访谈，他们即将到中小学实习．参与访谈学生情况见表5．

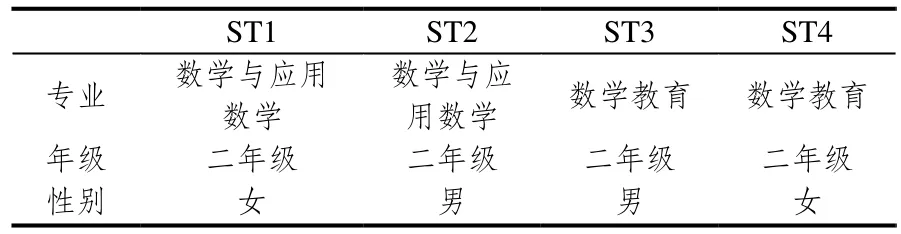
表5 参与访谈学生一览表

尽管师范特色的专业女生居多，在随机抽取访谈的对象时还是尽可能注意了男女比例，做到每个专业男女均衡．

对每个师范生的访谈主题也不尽相同，主要根据他们前测和后测问卷对比，每个师范生给出了不同的访谈提纲．以下访谈实录是根据现场录音整理而成．

TH这里指的是访谈老师，ST1、ST2、ST3、ST4是接受访谈的学生．

5.2 师生对话实录

（1）TH：你认为什么是教数学的好方法？

ST1：不能强迫孩子，逼孩子做数学题啊什么的，要让孩子喜欢，感觉有兴趣，这样孩子学起来才会越来越轻松．

TH：有道理．这个话题有点大．对，就是让孩子感兴趣．怎么才能让孩子感兴趣？

ST1：讲故事，做游戏，开展竞赛活动，联系生活实际，让学生动手操作，都能让学生感兴趣．

TH：不错．好的教学方法还有很多．

（2）TH：你认为下面的方法可以用于两数相乘吗？

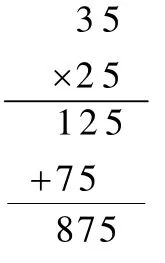
ST1：可以啊．

TH：可在第一次测试中你认为不可以，第二次又选了可以应用并推广，你是怎么想的？

ST1：第一次没看懂，不明白．第二次做问卷时想通了．主要是数学课程教学论课堂上见过此类问题．这个方法与通常的习惯不同，也是可行的．

TH：你的小学老师教过你这种方法吗？

ST1：没有，教材上也没见过．

TH：如果你遇见了小学生这样做，怎样处理？

ST1：我会告诉学生答案没有错，但不要这样做，这样不符合常规，也容易出错，做作业或考试还是按书上有的或老师教的方法．

TH：对，但一定要肯定学生的创造力．

（3）TH：在测试问卷中有一题，你有1.25元钱，如果你的这些钱加倍的话，你会有多少钱？请解答．

ST1：1.25´2=2.5，有2.5元钱．

ST1：不能，结果相同，但背景意义不同．

ST1：通过列式计算，发现结果相同，就想当然给出了结论，没有考虑实际背景．

TH：你的思想是如何变化的？

ST1：老师在数学课程教学论教学中，涉及了此类问题，我受到了启发．

（4）TH：

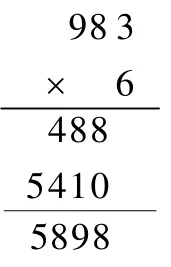
在前测中你认为结果正确只是偶然的巧合，此工作无规律可循，故不能推广．后测中你又认为这是一种位置跟踪算法，这种算法不同于一般算法，但也是对的．你的判读怎么发生了变化？

ST2：前测中还有点印象，当时就拿不定注意，没有看到规律，就蒙了一个答案．在后测中，我看懂了规律．

TH：平时老师的教学对你理解此问题是否有帮助？

ST2：老师在数学教学论教学中，也涉及了一些非常规算法的例子，这些算法也是有规律可循的，只是和教材上介绍的，老师教的方法不同．我还是从中领悟到道理．

TH：当你遇到学生用到非常规算法，你会怎么做呢？

ST2：我会问他（她）怎么想的，然后和他（她）一起讨论其中的道理．对于思维的闪光点我会鼓励表扬．

TH：班级中总有智力较好的孩子，遇见他们的非常规算法，一定要有耐心，保护好他们的好奇心是老师的责任．

你是怎么想的？

TH：前面的表达式好像也没问题．

ST2：沉默．

TH：上式中0L1表示一个数吗？

ST2：不表示一个数，0L1表示一类除以除数商为 0余1的数的集合．

TH：你怎么知道的？

ST2：在课堂试讲时有个同学讲的习题涉及了0L3，其中的道理是一样的．

ST2：不可靠，因为0L1不表示一个数．

TH：那你重新对该问题作出选择．

ST2：a）不是；b）不是；c）是

TH：看来现在真正理解了，你两次测试都没全对．

（6）TH：请你翻开测试问卷，看第五题，你两次都选了d），你是怎么想的？

TH：可是第一个饼全涂了色，第二个只涂了一份，怎么解释？

ST3：哦，……我也糊涂了．

TH：请你再读一遍题．

TH：看来不是不会做，是读题不认真．

ST3：是的，看图就想当然了．

TH：这样的问题看似马虎，其实还是缺少耐心．耐心也是我们做教师必备的素质．

ST3：我会注意的．

TH：如果你当了小学数学老师，你会怎样帮助学生认识“整体”？

ST3：多举一些实例，图形的、数字的、事物的，等等．

（7）TH：第十二题，第一次测试你选了b），第二次测试你又选择了d），你是怎么想的？

ST3：第一次测试时，我只考虑了这两堆苹果相比较的关系．后来在课程教学论的学习中，有同学试讲涉及了相关的问题，我知道了表示二者关系的情况很多，只要能用运算关系表达的，都表示二者之间的关系．

TH：所以第二次测试中就胸有成竹了，选择了d）

ST3：是的．

ST3：……其它运算关系也表示二者之间的关系．

TH：当然小学阶段学生不必考虑那么多，作为老师应该对此类问题有更深入的理解．

ST3：当老师真不容易，我觉得自己的知识面太窄，深度也不够．

TH：有这样的认识很好，认识到不足才能进步．

（8）TH：第三题，在第一次测试中你认为只有学生 B的方法对，学生A和学生C的方法不对．在第二次测试中，你认为学生A、B、C的方法都对．你是怎么想的？

ST4：学生B的方法是常规的方法，我们都会，都能明白．在第一次测试时，学生A、学生C的方法没有看懂，觉得很乱．经过一年课程教学论的学习，老师讲过此类问题．一些非常规算法，老师要求我们一定要看其中的道理，不能轻易否定非常规算法．这次仔细审题了，学生A学生C的算法也对，不是通常推广的方法．

TH：既然学生A学生C的方法都对，我们的教材为什么不介绍这些方法呢，老师在课堂上也不推广呢？

ST4：常规的方法简单，非常规的方法麻烦，规律不易找出来．

TH：你会如何对待学生的非常规算法？

ST4：如果正确，我会表扬鼓励，但是要求他（她）在作业或考试中还是要常规算法，常规算法比较简便，节约时间．

（9）TH：第六题中，你在前测中未选，在后测中选择了c），你是怎么想的？

ST4：在前测中，我没看懂什么意思．后测中看明白了，图c）与其它图形有明显的不同，其它都是同类图形的比较，图c)左右两个图属于不同的类别，一个长方形，一个圆形，没有可比性．

TH：平时老师的教学对你是否有启发？

ST4：有的．在同学们习题展示时，有个同学讲了一个相关的问题，老师组织同学讨论了．所以记忆比较深．

TH：这里体现了一个什么思想？

ST4：分类的思想．

TH：对，分类的思想在数学中常见到．

访谈对话涉及了调查问卷14个项目中的8个问题，4个师范生根据访谈老师的提问谈了自己的认识和感受．他们的教育观念比较符合现代教育理念，这应该与数学课程论的学习有关．他们的数学基本功较好，经过高考选拔，能够报考并且录取到数学专业的学生数学基本素养能够满足未来中小学数学教师的需要．师生对话反应了在这一年师范生对测试问题的思想变化主要源于数学课程教学论任课教师的指导．访谈只涉及到师范生的 SCK，问题举例仅限于小学数学的数与运算．从访谈结果来看，研究者的数学课程教学论教学对学生 SCK的提高是有效的，同学们是用心学习的．这与问卷测试分析的结果也相吻合．

比如TH和ST1、ST4关于测试问卷中第三题的对话，反应了ST1、ST4对非常规算法认识的变化，也说明他们在第一次测试中对此问题的陌生，经过数学课程论的学习，对处理此问题有了较为深刻的认识．针对测试问卷中的第三题，在前测后测中数学教育专业的师范生做对人数的变化从34.4%上升到 54.1%，数学与应用数学专业的师范生做对人数的变化从13.2%上升到54.4%．ST1、ST4对此类问题的认识变化仅代表了一部分同学的进步．

从整体访谈和测试也可以看出师范生SCK的缺乏和数学课程论教学存在的问题．

6 总结和反思

6.1 总 结

通过实验数据分析、学生访谈，可以得出以下结论：在数学课程论教学中，研究者的教学是有效的，能够提升数学师范生的 SCK．这两个专业的学生数学基本功是扎实的，但作为未来数学教师应具有的SCK却不怎么理想，还有很大上升的空间．

按照Ball等学者的划分，面向教学的数学知识（MKT）有6个维度，选择了其中一个维度SCK对数学师范生进行调查研究．从相关文献来看，更多学者研究了数学教师的PCK．近几年来西方学者对数学教师的SCK也有研究，并用Ball等早期开发的LMT（学习教数学）工具作为测试数学教师SCK的工具．在不违背设计者意图的情况下，根据国情对这套测试工具进行适当改编，作为该研究的工具．经检验，这套工具测试的结果大体反应了实际情况．虽然SCK只是MKT的一个维度，从对SCK的界定来看，教师拥有SCK的水平直接影响了他们的教学水平，从而影响了教学效果．因此选择SCK这一视角探讨数学师范生的专业发展．

6.2 反思和进一步研究的问题

（1）该学年除了开设数学课程教学论的课程，同时也开设了其它的课程，其它课程虽然与数学师范生SCK的关联没有那么密切，但也不能排除其它学科对数学师范生 SCK的影响．

（2）由于该学年学校没有安排学生见习，学生尚未经过教育实习，教育见习、实习对学生 SCK的影响都没有考虑．还有部分学生做家教，也不知家教辅导的经历对数学师范生的SCK影响有多大．这些都是研究者后续研究的内容．

（3）数学师范生的SCK是薄弱的，虽然经过数学课程教学论的学习有了明显的提高，测试结果并不乐观．因此数学课程教学论的授课内容、方法、手段还有待于改进．

（4）数学课程教学论的授课采用了自编讲义，参考了国内外大量文献资料，由于研究者学识水平有限，可能也影响了学生的SCK的发展．进一步优化授课讲义也是继续进行的工作．

（5）参与测试的学生都是大学二年级的学生，很多相关学科还未学习，该学年开设数学课程教学论是否是最佳时间也值得商榷．

（6）数学师范生意念中的小学数学教学受到自己小学数学老师的影响，他们小学数学教师的SCK是否也影响数学师范生的SCK，以及当前小学数学教师的SCK如何，这些都是继续研究的问题．

[1]Shulman L S. Those Who Understand: Knowledge Growth in Teaching [J].Educational Researcher, 1986, 15(2): 9.

[2]Ball D L, Bass H. Interweaving Content and Pedagogy in Teaching and Learning to Teach: Knowing and Using Mathematics [A]. In: Boaler J.Multiple Perspectives on the Teaching and Learning of Mathematics[C]. Westport, CT: Ablex, 2000.

[3]Ball D L, Thames M H, Phelps G. Content Knowledge for Teaching: What Makes It Special [J].Journal of Teacher Education, 2008, 59(5): 389-407.

[4]Ball D L, Bass H, Boerst T, et al. Developing Teachers’ Mathematical Knowledge for Teaching [Z]. Paper Presented at the Mathematics Focus Session, University of North Carolina, Chapel Hill, NC, 2008.

[5]Hill Heather C, Blunk Merrie L, Charalambous Y, et al. Mathematical Knowledge for Teaching and the Mathematical Quality of Instruction: An Exploratory Study [J].Cognition & Instruction, 2008, 26(4): 430-511.

[6]Hill H C, Lubienski S T. Teachers’ Mathematics Knowledge for Teaching and School Context: A Study of California Teachers [J].Educational Policy, 2007, 21(5): 747-768.

[7]Morris A K, Hiebert J, Spitzer S M. Mathematical Knowledge for Teaching in Planning and Evaluating Instruction: What can Preservice Teachers Learn [J].Journal for Research in Mathematics Education, 2009, 40(5): 491-529.

[8]Susan Swars, Lynn C Hart, Stephanie Z Smith, et al. A Longitudinal Study of Elementary Pre-service Teachers’Mathematics Beliefs and Content Knowledge [J].School Science and Mathematics, 2007, 107(8): 325.

[9]Hill Heather C, Ball Deborah Loewenberg. Learning Mathematics for Teaching: Results from California’s Mathematics Professional Development Institutes [J].Journal for Research in Mathematics Education, 2004, 35(5): 330-352.

Research on Development of SCK of Math Students in Normal University——The Number and the Operation as an Example

WANG Ai-ling1,2
(1. East China Normal University, Shanghai 200241, China；2. Heze University, Shandong Heze 274015, China)

In this paper, based on mathematical teaching theory course, number and operation content in elementary school as an example, investigates development of SCK of math students in normal university. The study found that: mathematics curriculum teaching theory teaching can effectively promote the growth of SCK of math students in normal university. But SCK of math students in normal university is still weak, needs to be improved, and analyzes the factors affecting the development of SCK of math students in normal university.

specialized content knowledge (SCK); mathematics curriculum teaching theory; math students in normal university; professional development

G652

A

1004–9894（2017）01–0098–05

[责任编校：周学智]

2016–10–13

上海市核心数学与实践重点实验室基金项目——数学实践（13dz2260400）；山东教育科学规课题“高等教育数学教学专项”——数学史融入高等数学教学案例之研究（YBS15016）

王爱玲（1969—），女，山东菏泽人，菏泽学院教授，华东师范大学博士生，从事数学课堂教学和数学解题研究．