基于质量监测的初中学生逻辑推理发展状况的调查研究

周雪兵

（南京市金陵汇文学校，江苏 南京 210036）

基于质量监测的初中学生逻辑推理发展状况的调查研究

周雪兵

（南京市金陵汇文学校，江苏 南京 210036）

逻辑推理是数学核心素养的基本成分．在2016年江苏省中小学生学业质量监测测试中，对与逻辑推理相关的题目得分及水平分布作了统计和分析，结果表明：（1）江苏省初二年级学生的6个数学核心素养的发展不平衡，逻辑推理水平在6个核心素养的发展中处于中等水平．（2）江苏省初二年级学生的逻辑推理水平表现依次是城区好于镇区，镇区好于乡村；苏中好于苏南，苏南好于苏北；民办学校明显好于公办学校；不存在性别上显著差异．（3）将逻辑推理分为演绎推理和合情推理，初二年级学生演绎推理水平优于合情推理水平．

数学核心素养；逻辑推理；初中生；学业质量监测

1 问题提出

高中课程标准修订组专家提出6个数学核心素养成分，逻辑推理是其中之一．具体描述为：逻辑推理是指从一些事实和命题出发，依据逻辑规则推出一个命题的思维过程．主要包括两类：一类是从小范围成立的命题推断更大范围内成立的命题的推理，推理形式主要有归纳、类比；一类是从大范围成立的命题推断小范围内也成立的推理，推理形式主要有演绎推理．逻辑推理是得到数学结论、构建数学体系的重要方式，是数学严谨性的基本保证，是人们在数学活动中进行交流的基本思维品质．在逻辑推理核心素养的形成过程中，学生能够发现问题和提出命题；能掌握推理的基本形式，表述论证的过程；能理解数学知识之间的联系，建构知识框架；形成有论据、有条理、合乎逻辑的思维品质，增强数学交流能力．

《义务教育课程标准》对推理能力的描述是：推理能力的发展应贯穿在整个数学学习过程中．推理是数学的基本思维方式，也是人们学习和生活中经常使用的思维方式．推理一般包括合情推理和演绎推理，合情推理是从已有的事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果；演绎推理是从已有的事实（包括定义、公理、定理等）和确定的规则（包括运算的定义、法则、顺序等）出发，按照逻辑推理的法则证明和计算．在解决问题的过程中，合情推理用于探索思路，发现结论；演绎推理用于证明结论[1]．

两种描述，尽管名称各异但本质相同，指的就是数学推理能力．数学是思维的科学，数学推理作为一个数学核心素养是名正言顺的[2～4]．其实，虽然逻辑推理作为一种数学核心素养提出，但这并不是一个新的概念，推理历来是认知心理学和数学教育学研究的话题，林崇德先生在中小学生逻辑思维能力的发展方面作了大量研究，得到一些有价值的结果[5]．那么，当下初中学生的逻辑推理能力是一个怎样的状况？特别是逻辑推理作为核心素养提出又一次成为数学教育研究的关注点，有必要对这个问题作研究．

这里就2016年江苏省初中二年级学生数学学业质量监测中，与逻辑推理相关的题目得分情况和水平分布作出分析，以反映江苏省初中二年级学生逻辑推理水平的基本状况．为了统一起见，把推理能力、逻辑思维能力、数学推理等名称统一用逻辑推理．

2 调查结果

2.1 不同群体在逻辑推理各水平的分布

图1给出了江苏省及不同群体学生在逻辑推理各水平上的人数比例．

图1 不同群体学生在逻辑推理各水平上的人数比例

从图1中可以看出，在数学核心素养之逻辑推理上，江苏省学生在不合格水平上的人数比例为13%，说明江苏省有87%的学生达到了合格及以上水平．城区、镇区和乡村学校学生在不合格水平上的人数比例分别为11%、14%和20%；苏南、苏中和苏北学校学生在不合格水平上的人数比例分别为10%、9%和17%；公办和民办学校学生在不合格水平上的人数比例分别为14%和 5%；男生和女生在不合格水平上的人数比例分别为13%和11%．

2.2 题目中涉及逻辑推理的得分情况

从表1中可以看出，测试卷中共有11题重在体现数学核心素养的逻辑推理要素，选择题有1题，填空题有6题，解答题有4题．其中第16、18题各设置了3个小题进行考查，第15、17题各设置了2个小题进行考查；表1中的A水平、B水平、C水平、D水平分别表示优秀、良好、合格、不合格4种水平的学生．从表1中可以看出，该次测试中，学生总体能力处于A、B、C、D四个水平的学生在M8AO061题上的平均得分率分别为92.9% 、66.3%、42.8%和27.9%；从学生的平均得分率分布情况看，在17个小题中，学生表现优异的小题有6个，表现中等的小题有10个，表现较弱的小题有1个．

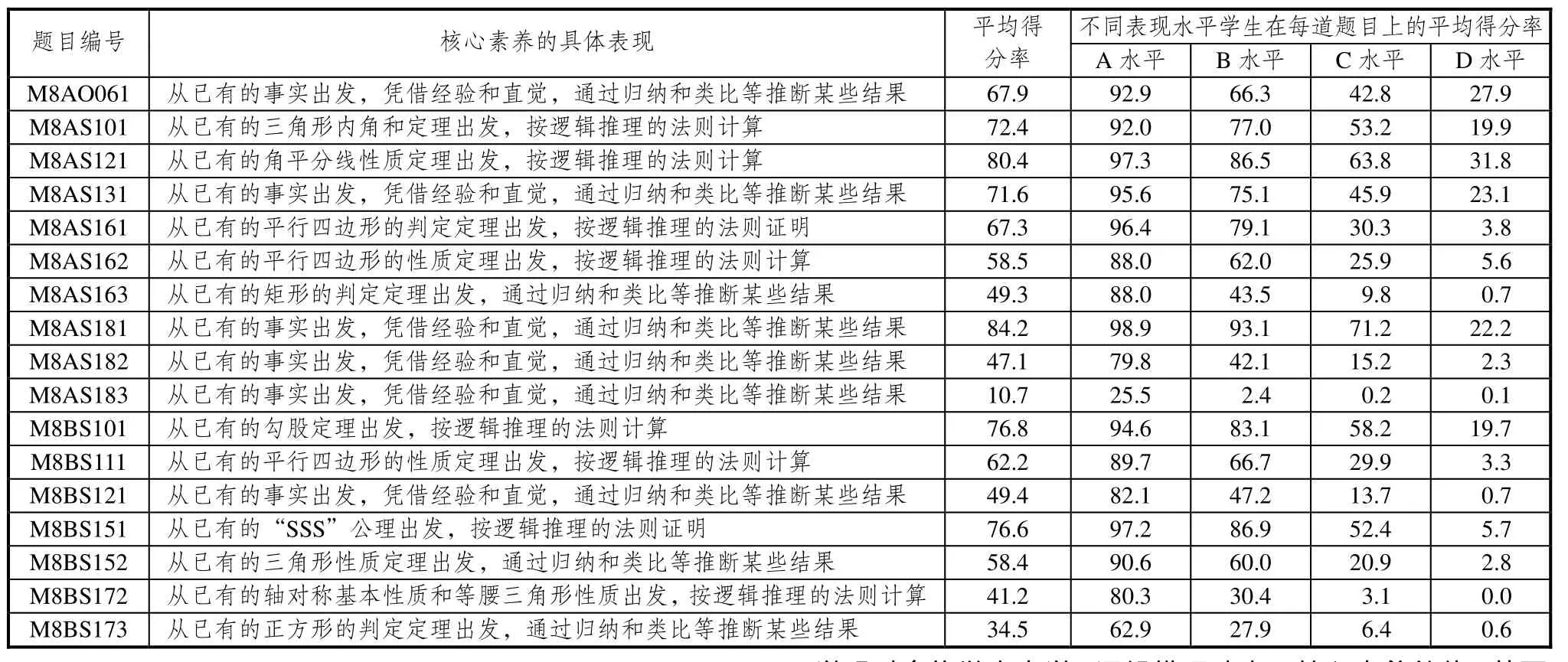
表1 学生学业质量监测中逻辑推理在各小题中的分布情况

3 分析讨论

3.1 不同表现水平学生在每道题目上的平均得分率比较

从调查结果看，学生在以下6个方面表现优异：（1）从已有的事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果；（2）从已有的角平分线性质定理出发，按逻辑推理的法则计算；（3）从已有的勾股定理出发，按逻辑推理的法则计算；（4）从已有的“SSS”公理出发，按逻辑推理的法则证明；（5）从已有的三角形内角和定理出发，按逻辑推理的法则计算；（6）从已有的事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果．但是在两个方面表现较差，即（1）从已有的正方形的判定定理出发，通过归纳和类比等推断某些结果；（2）从已有的事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果．这个结果说明，初中学生的演绎能力好于合情推理能力，即初中二年级学生的演绎能力发展水平高于合情推理能力，这是一个值得关注的问题．

4个水平的学生在每道题目上的平均得分率基本呈正态分布，其中优秀、良好水平学生平均得分率低于20%的题有1道，合格水平学生平均得分率低于10%的题有4道，不合格水平学生平均得分率低于1%的题有9道．

3.2 逻辑推理与6个核心素养总体情况的比较

从两者优秀的得分人数占比看，在所统计的11项数据中，其中有9项相同，仅有城区与苏中两项落后1%，说明对优秀学生来说，逻辑推理与核心素养总体情况高度一致．从两者良好的得分人数占比看，在所统计的11项数据中，最大差为 6%，最小差为 4%，说明对良好学生来说，逻辑推理低于核心素养总体．从两者合格的得分人数占比看，在所统计的11项数据中，最大差为3%，最小差为0%，说明对合格学生来说，逻辑推理略高于核心素养总体．从两者不合格的得分人数占比看，从所统计的11项数据看，最大差为 5%，最小差为 2%，说明对不合格学生来说，逻辑推理远低于核心素养总体．

这个结果说明，与其它5个核心素养的发展相比较，逻辑推理的水平相对较低，这可能是受到合情推理水平不高的影响所致．

3.3 逻辑推理自身的差异性比较

城乡比较：从优秀的得分人数占比与不合格的得分人数占比看，逻辑推理的表现城区要远好于镇区，镇区要好于乡村；从良好的得分人数占比与合格的得分人数占比看，城区、镇区、乡村的逻辑推理表现大致相当．

不同地域比较：从优秀的得分人数占比与不合格的得分人数占比看，逻辑推理的表现苏中要好于苏南，苏南要好于苏北；从良好的得分人数占比与合格的得分人数占比看，逻辑推理的表现苏南、苏中、苏北大致相当．

不同性质学校比较：从优秀、良好、合格、不合格的得分人数占比看，逻辑推理的表现民办要好于公办．

不同性别比较：从优秀的得分人数占比与不合格的得分人数占比看，逻辑推理的表现男生略好于女生；从良好的得分人数占比与合格的得分人数占比看，逻辑推理的表现男生与女生基本相同．

从以上结果看出，男女学生在逻辑推理水平上没有差异．乡村学校和苏北地区的学校初中二年级学生的逻辑推理水平相对较低，民办学校的学生在逻辑推理水平方面较许多公办学校更有优势．这是教育公平问题要思考的问题．

3.4 出现的问题分析

研究者对平均得分率为10.7%与34.5%的两个小题，进行了典型错误的记录，并对错因进行项目组的讨论与分析．

案例1 M8AS183 小明说：“我还能将任意一个四边形纸片剪拼成一个等面积的矩形”，请你帮小明在图中画出示意图并简要说明做法．

错误分析：

（1）会画图但不会解释，数学表达欠缺；

（2）会画图但解释不清晰或不完整，能正确运用转化思想，语言描述简介，但还不够严谨；

（3）作图不规范，明显不是中点，说明答题规范性不够；

（4）只会简单模仿，未能明晰要求，未能迁移应用，基本活动经验不足；

（5）认为边长相等或平行去构造，未能进行验证，思维的严谨性不够；

（6）只裁剪不拼接，说明未能读懂试题要求，理解能力欠缺．

案例 2 M8BS173△ABC如图所示，点A关于BC所在直线的对称点是点D．当△ABC满足什么条件时，四边形ABDC是正方形？请说明理由．

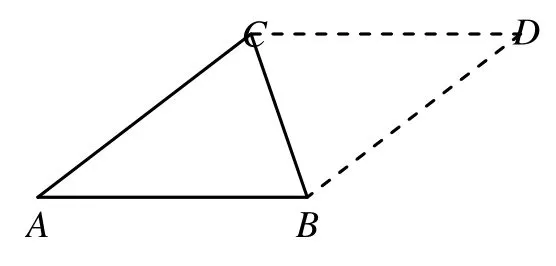
错误分析：

（1）对称概念不清，不能利用对称得到对应边或对应角相等；

（2）只说出了△ABC是等腰直角三角形，没有具体提出哪个角是直角；

（3）对正方形的判定条件理解不足，出现了AB＝AC或∠A＝90°就得到四边形ABDC是正方形的错误论断；

（4）对此类问题的答题逻辑不清晰，出现了假设四边形ABDC是正方形，从而得到△ABC形状的书写过程；

（5）只出现结论，但不能对结论时行证明，不会写推理过程；

（6）逻辑推理过程不规范，对三段论的掌握出现逻辑混乱的现象．

4 结论与建议

4.1 结 论

（1）江苏省初二年级学生的6个数学核心素养的发展不平衡，逻辑推理水平在6个核心素养的发展中处于中等水平．

（2）江苏省初二年级学生的逻辑推理水平表现依次是城区好于镇区，镇区好于乡村；苏中好于苏南，苏南好于苏北；民办学校明显好于公办学校；不存在性别上显著差异．

（3）将逻辑推理分为演绎推理和合情推理，初二年级学生演绎推理水平优于合情推理水平．

4.2 建 议

（1）要改变模仿的记忆式的教学方式，让学生利用操作、实验等活动进行联想、归纳、类比、猜想，发展学生的合情推理能力．

（2）要有意识地训练学生演绎推理能力，将形式逻辑的相关知识渗透到教学中，规范三段论的思考，培养学生言必有据的思维习惯．

（3）教学中，在注重证实的同时要将证伪的思想融入其中，将证明一个事实为真与证明一个事实为假相结合，培养学生的创新性思维．

[1]中华人民共和国教育部．义务教育数学课程标准（2011版）[M]．北京：北京师范大学出版社，2011．

[2]喻平．数学学科核心素养要素析取的实证研究[J]．数学教育学报，2016，25（6）：1．

[3]王光明，张楠，周九诗．高中生数学素养的操作定义[J]．课程·教材·教法，2016，（7）：50．

[4]郑毓信．数学教育视角下的“核心素养”[J]．数学教育学报，2016，25（3）：1．

[5]林崇德．学习与发展——中小学生心理能力发展与培养[M]．北京：北京师范大学出版社，1999．

Investigation on Development Status of Middle School Students’ Logical Reasoning Based on Quality Monitoring

ZHOU Xue-bing
(Nanjing Jinling Huiwen School, Jiangsu Nanjing 210036, China)

Logical reasoning is one of the basic elements of mathematics key competencies. During elementary and middle school student’s education quality monitoring examinations in Jiangsu Province in year 2016, statistics & analysis were held concerning scores and performance distribution of exam questions related to logical reasoning. The results indicate that: (1) In Jiangsu Province, the development of Grade 8 students’ six mathematics key competencies is not balanced, among which logical reasoning is at medium level. (2) Among Grade 8 students’ logical reasoning performance in Jiangsu Province, it appears that urban area is higher than township, township is higher than countryside; mid-Jiangsu region is higher than southern Jiangsu, southern Jiangsu is higher than northern Jiangsu; private schools are significantly higher than public schools; while no significant difference in gender is found. (3) When logical reasoning is classified into deductive reasoning and reasonable inference, Grade 8 students’performance of deductive reasoning is higher than that of reasonable inference.

mathematics key competencies; logical reasoning; middle school students; education quality monitoring

G632

A

1004–9894（2017）01–0016–03

[责任编校：周学智]

2017–01–20

江苏省教育厅基于测试分析的跟进式改革重大研究项目——义务教育学科核心素养和关键能力研究（2015JYKTZD-02）；江苏省中小学教学研究第十一期重点课题——初中数学学业水平评价研究（2015JK11-Z085）；江苏省社科基金——中小学生数学核心素养体系建构与教学实践研究（15JYD001）

周雪兵（1973—），男，江苏南京人，中学高级教师，主要从事数学教育研究．