中学数学课堂教学行为关键性层级研究

曹一鸣，于国文

（北京师范大学 未来教育高精尖协同创新中心，北京 100875）

中学数学课堂教学行为关键性层级研究

曹一鸣，于国文

（北京师范大学 未来教育高精尖协同创新中心，北京 100875）

“关键教学行为”层级是对课堂教学行为重要性进行分级与研究．探寻关键教学行为对于抓住教学研究与改进中的核心问题，促进有效教学具有积极意义．基于中学数学课堂教学词典（Lexicon）项目资料，经专家论证，得到 124个教学行为．借助CIT（Critical Incident Technique）技术，结合专家评判，提炼出16个关键教学行为．进一步运用问卷调查和访谈，得出中学数学课堂上关键性最高的 A层教学行为：师生互动、教师提问、教师展示、学生听讲以及学生做题．其余教师讲解、学生讲解、学生提问、合作学习等11个关键教学行为属于B层；其余108个教学行为归入C层级．

关键教学行为；CIT；中学数学课堂教学词典项目；问卷调查；访谈

2000年以来，16个国家和地区的近百名研究人员进行的“学习者视角的国际课堂教学研究（The Learner’s Perspective Study，简称LPS）”引起了广泛关注，同时研究者也发现了跨文化研究过程中的固有困境之一：课堂活动的多样性造成一些活动术语缺失[1]，为此北京师范大学曹一鸣教授和墨尔本大学David Clarke教授联合中国、澳大利亚、美国、日本、法国、德国、芬兰、智利、捷克等9个国家发起中学数学课堂教学行为词典项目（The Lexicon Project: Analysing pedagogical naming systems from different cultures to reconceptualise classroom practice and advance educational theory，简称Lexicon Project），以专门研究各国中学数学课堂教学过程中的专业术语，用来描述课堂中的教学行为．

对教学行为的研究，完善教师教学行为品质，是教师成为现代教育教学理念促进者的最为基础的、也是重要的条件[2]．当前国内已有研究中对于课堂内外以及教师专业成长等过程中的关键事件的研究很多，关键性教学时事件对于指导教师教研具有一定作用[3]．2005年以来，上海市教科院由顾泠沅教授领衔，对关键教育事件进行了系统研究．上海市长宁区教育学院借鉴国内外关于“关键事件”、“关键教学事件”等一系列理性探索和实践尝试，在国内较早开展了以课堂教学为主的关键教育事件的教师教育行动研究，并举办研修专题培训[4～5]．关键事件最终落实到具体行为上，所以，研究着眼于探究具体教学行为本身的关键性．

基于中学数学课堂教学行为词典项目，进一步对中学数学课堂上教学行为的关键性进行层级研究．对于教学行为的关键性层级研究受启发于国内外对关键教育事件的研究．课堂中的关键事件以及关键教学行为（CPB：Critical Pedagogical Behavior）对整个课堂的高效有序运行以及学生知识习得发挥着重要作用．教学行为的关键性是对一个课堂教学行为重要性的解释；将某行为称为关键教学行为是一种价值判断，这种判断的基础就是附着在这一行为之上的重要性．研究的目的在于探寻中学数学课堂教学中的关键教学行为．

1 研究背景：中学数学课堂教学行为词典项目

中学数学课堂教学行为词典项目的研究目标是梳理各国中学数学课堂教学行为术语，厘清其概念，并关注各国家之间的异同，最终汇编形成国际中学数学课堂教学词典，词典中的每一个术语指向具体的课堂教学行为，并包括对这一行为的描述．该项目在9个国家各挑选一名优秀教师进行三机位录像：教师机位、学生机位和课堂全景机位（见图1），并将三机位的录像以及转录文字在一个界面上合成显示．3名教师共摄制3节课，从中选取第三节作为研究对象．

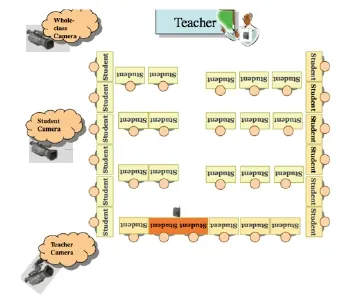
图1 中学数学课堂教学行为词典项目三机位录像

每个国家团队观察录像中的课堂活动，并在已有的教学语言系统之中找到对这一课堂活动的表述，记录每一个活动的开始和结束时间、活动的名称和描述，翻译成英语的过程中需保证该活动的核心特点得以呈现．

中学数学课堂教学行为词典项目进展过程中，各国对于各自中学数学课堂教学词典广泛征求各国内意见并标注每一术语的“熟悉度”和“使用频率”，从而发现一个共同问题：初步形成的各国教学词典中的术语在“熟悉度”和“使用频率”表现出一定的层级性．鉴于此，试图对中国中学数学课堂教学词典中的术语进行关键性层级研究．

2 研究方法

基于中学数学课堂教学行为词典项目的视频资料以及项目生成的124个中国中学数学课堂教学行为，借助关键事件技术（CIT：Critical Incident Technique）以提炼课堂教学中的关键教学行为，进而使用Polinode在线软件进行教学行为的层级分类．

关键事件技术CIT是一种定性研究方法，“它直接观察人类行为的一系列程序，其目的是促进他们解决实际问题和开发潜能”．其研究对象是关键事件（CI），CI可以被理解为那些“特定的、可观测的人类活动”[6]．1993年David Tripp教授在其所著的Critical Incidents in Teaching—Developing Professional Judgement一书中系统提出教育研究中的关键事件研究[7]．借助CIT，可以将关注的焦点集中在课堂教学中的关键行为，并对此进行反思、建立该关键教学行为与有效教学之间的关联，继而借助对关键教学行为的提炼与思考，促进指导有效教学．

使用 CIT时在传统流程之上稍作改变，对于关键教学行为的鉴别区别于传统 CIT借助“故事”、“经历”和“事件描述”[8]等进行鉴别的方法．为适应具体研究要求，对CIT进行改进，具体操作流程如下：（1）确立研究目标；（2）观看 Lexicon项目录像课，编码并提取教学行为；（3）专家论证，精简并提取“关键教学行为”；（4）开发研究工具，设计调查问卷并进行信度和效度检验；（5）面向教学经验丰富的一线教师执行问卷调查以及访谈以鉴别关键教学行为；（6）呈现、分析并解释结果．

3 研究过程

3.1 确立研究目标

首先根据上述操作流程，确立研究目标：借助 CIT方法，在中学数学课堂教学词典项目的基础之上，结合专家论证和面向经验丰富的一线教师的问卷调查，探寻并提取中国中学数学课堂教学中的关键教学行为，使用Polinode软件将教学行为之间的联系进行可视化，依据可视化的教学行为之间的关联程度实现对教学行为进行层级分类．

在层级界定过程中，首先对教学行为之间建立结构上的联系，得到课堂关联指数CIC（CIC：Correlation Index in Class:研究将与某教学行为相关的其它教学行为的数量定义为该教学行为的课堂关联指数），关联指数低于3的教学行为与其它教学行为之间的关联脆弱，联系度低，从而对于整个课堂的影响度小，从关联其它教学行为进而影响整个课堂的角度来看，其“关键性”最低，基于CIC，可将这些教学行为归为一类，定为层级C，共计108个教学行为，将除此之外的16个教学行为界定为“关键教学行为”全部归入层级分布中的A级和B级．对于层级A、B、C的界定如下：

A层级：在关键性排在最高位置，表现在实践和交流中的高使用频率、相对较高的教学上的重要性以及与其它教学行为之间较高的关联度．

B层级：关键性居中，在实践和交流中的使用频率以及教学上的重要性略低于 A层级，与课堂中的其它教学行为之间的关联度较高．

C层级：关键性最低，主要表现是与课堂中的其它教学行为之间的关联度低或者无关联，行为本身相对孤立．

3.2 基于中学数学课堂教学行为词典项目提取教学行为

中学数学课堂教学行为词典项目共有来自9个国家的9节八年级录像课，项目组研制了从录像课中提取教学行为术语的方法：以中国为例，项目组内成员共同观看中国录像课，并初步形成一个教学行为列表，继而分组观看其他8个国家的录像，保证每节录像由至少两人观看、编码，并在已形成的教学行为列表的基础之上进行补充和完善．

CIT对于关键事件收集的标准，此处提取课堂教学行为的标准是出现冗余：每生成100个教学行为，至多出现2～3个新的教学行为[7]．由于录像课未能充分囊括中学数学课堂教学行为，研究团队在对9个国家的课堂录像进行教学行为提取时，仅提取40（40/124）个教学行为，且视频源数据的饱和度在中国、法国、澳大利亚3个国家的教学行为提取后基本达到（占比最高0.32，该3个国家采集数达到0.29），见表1．中学数学课堂教学行为词典项目操作中继续约请6位领域内专家以及有丰富一线教学经验的中学数学教师或者教研员进行专家审核，专家论证已使得占比达到0.9，之后增速放缓，直至达到饱和状态，出现冗余．该环节旨在对初步形成的教学词典进行补充，通过对冗余率的计算，符合CIT的冗余标准，接受视频提取和6位专家审核增删之后的中国中学教学课堂教学词典，共包含教学行为124个，是研究的基础．

表1 报告教学行为数目及占比

3.3 专家论证精简并提取“关键教学行为”

整个课堂是一个有机整体，教学行为之间也存在着紧密的联系，因而研究者进一步构建教学行为之间的联系，根据联系的程度，建立教学行为的课堂关联指数 CIC探寻课堂教学中存在的相对更为“关键”的行为．此处关键的含义是，该行为与更多其它教学行为存在联系，使得该行为在整个课堂教学之中具有更高的“牵一发而动全身”的影响力．

在2015年11月于澳大利亚墨尔本大学召开的中学数学课堂教学行为词典项目会议期间，来自9个国家的专家肯定了这一建立教学行为之间的联系与结构的想法，并提出课堂关联指数CIC可依据这些关系进行：

（1）从属（hierarchical）；

（2）顺序发生（sequential）；

（3）同时发生（coincident）．

根据以上几个角度建立中国中学数学课堂教学行为词典中各行为之间的结构（Chinese Lexicon Structure）．结构建立的主要流程为：首先依据行为主体（教师、学生或者师生共同进行）建立一级维度；进而对教师行为、学生行为以及师生共同进行的行为进行划分类别以建立二级维度；最后，将所有124个教学行为归入二级维度之下，形成从属结构图．在从属结构的基础之上，再进一步根据课堂教学之中行为之间的发生顺序建立3种关系：顺序发生；同时发生；无时间上的关系（这种情况不标注）．至此，建立124个教学行为之间的关联结构，此处结构的建立采取了 CIT方法中的分类论证，将124个教学行为分为15类．

继而约请3位专家学者对研究所建立的结构进行论证，这也是 CIT信度检验的重要方法之一，在论证的基础之上建立了中国中学数学课堂教学行为词典中各行为之间的结构（Chinese Lexicon Structure），作为中学数学课堂教学行为词典项目的研究成果之一，展示了某教学行为与其它教学行为之间的联系．3位专家教师具有丰富的一线教学经验以及进行数学教育领域相关研究的理论素养与研究功底，经过他们论证的中国中学数学课堂教学词典结构及其中各教学行为之间的联系具有颇高的信度．表2呈现了专家之间以及各专家与研究者初始建立的分类之间的一致率（Agreement Rate）．

表2 报告Agreement Rate

通过表 2可知专家之间的一致率以及专家与研究者分类之间的一致率基本达到可接受的程度（>0.8），通过项目研究者与参与专家的再商讨以及专家之间的讨论协商，将独立见解进行合并，并继续论证合并后的结构，3个角度的Agreement Rate继续上升，均超过了 0.9，基本形成稳健结构．

同时，可借助Perreault教授和Leigh教授的分类信度指数公式（公式A）[10]进一步考察分类系统的稳定性和一致性．

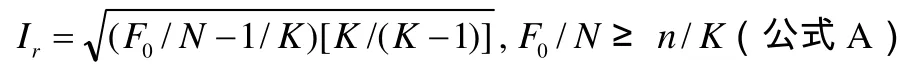
公式A中，Ir表示的是分类信度指数；F0为彼此同意的数目；N为评判的总数；K为类别数．当指数Ir≥0.8时，可以判定分类的综合信度良好．经计算，一级维度、二级维度以及时间关系维度的信度指数分别为0.99、0.79、0.9，平均为0.89，具有很高的信度．继而，借助Polinode在线软件，最终形成教学行为结构如图2．

基于该结构，并再次借助Polinode软件，可以清晰直观地获知各教学行为的课堂关联指数CIC如表3，并将表3中的教学行为定为“关键教学行为”，归入层级分布中的A级和B级．

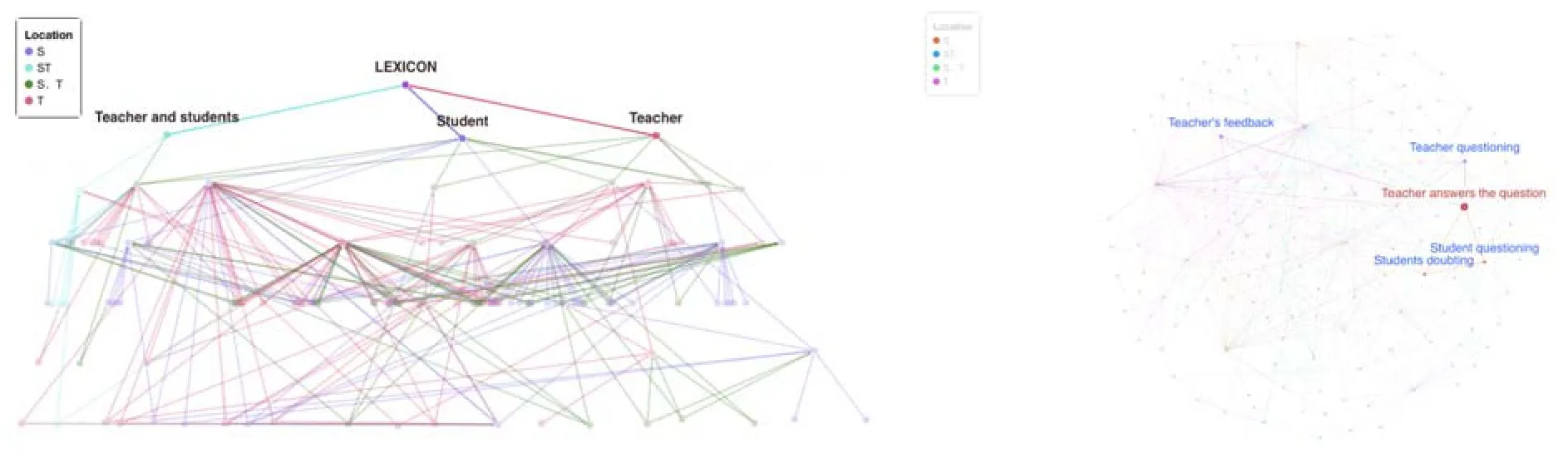
图2 中国中学数学课堂教学行为结构

表3 课堂关联指数及关键教学行为

3.4 进一步开发与完善研究工具

为了进一步调研中学课堂上的关键教学行为，研究开发了半结构式调查问卷，以面向一线教师进行调查．并对问卷的信度（Reliability）和效度（Validity）进行检验．

首先，借助霍尔斯蒂（Holstior）公式（公式 B）[11]，测定5名评判专家之间的信度．

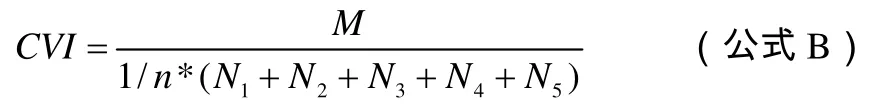
公式B中，R为信度指数；n为评判专家人数；M为共同接受的数目；Ni(i=1, 2, 3, 4, 5)为各个评判专家对某一列的评判数目，在研究中，各列均为16个教学行为以供评判，5位专家的N值始终为16．霍尔斯蒂公式以0.8为界限，不低于 0.8则表明专家之间具有较好的一致性．计算可得，5位专家之间的信度指数R值为 0.90（其中，R1=0.88，R2=0.94，R3=0.88，Ri(i=1, 2, 3)表示第i个角度的专家信度指数），超过了标准参考值0.8，表明专家之间具有很好的一致性．同时，可以计算每两个专家之间的信度指数值，均在0.90以上，表明专家两两之间的信度较高．

已保证专家间信度的基础之上，论证了该问卷的内容效度．依据各专家对于问卷设置的各条目给与“接受”（记 1分）或者“不接受”（记0分）的判断，可以进行问卷的内容效度检验，在 Polit的内容效度检验指数（CVI: Content Validity Index）[12]的基础上，根据评判专家的人数，调整原公式（）制定了契合研究实际情形的拓展公式（公式C）：

公式C中，CVI表示所求的内容效度指数；nij表示问卷设置中第i名专家对第j个因子与整个问卷的相关度评判：专家接受则相关度为1，专家不接受则相关度为0；N表示评判专家人数．调查问卷中每一列的每一个因子，均需要5名专家独立判别与待研究问题的相关度．利用公式 C分别计算问卷中 3列的内容效度指数可得：CVI1=0.95，CVI2=0.98，CVI3=0.95，计算3列内容效度指数的均值作为整个问卷的综合CVI，可知，达到推荐的0.9标准参考值，综合效度良好．

3.5 进行问卷调查以及访谈以探寻关键教学行为

采取随机抽样的方式进行该问卷调查，共发出问卷124份，回收124份，回收率100%．去除不规范、低信度、无效样本17份，样本有效率86.29%，其中有10年以上教龄的样本72份，占有效样本的67.29%，教学经验丰富的教师样本一定程度上巩固了所获取的关键教学行为的信度．

在问卷分析的基础之上继续对 4名教学经验丰富的特技、高级一线教师进行访谈以论证初步获取的关键教学行为的“关键性”．

3.6 呈现分析并解释结果

经上述问卷调查后，对于每一个样本将得到3个数值，分别为该样本对这16个教学行为进行在课堂实践中的使用频率、交流表达中的使用频率以及教学中的重要性排序．进而研究将依据这3组数据确定关键教学行为．

前文已指出关键教学行为是对一个课堂教学行为的重要性的解释，将某行为称为关键教学行为是研究者的一种价值判断，而这种判断的基础就是附着在这一行为之上的重要性．这种重要性主要借助在实践以及交流之中的使用频率呈现．通过对部分教师的访谈发现，有一些教学行为其重要性得分很高，但在课堂之中却未必能很好落实，或其重要性可以借助课外等非课堂的情境和媒介展现，则对于整个课堂教学而言，其“牵一发而动全身”的功效就不甚明显，即其关键性表现得不是很明显；类似地，有一些教学行为无论是在课堂上还是在日常交流中都频繁出现，但是其教学上的重要性得分却未必高，这样的教学行为只能被称之为高频行为，进一步研究探寻之前不能将其称之为关键行为．

综上，综合实践、交流、教学上的重要性3个角度进行关键教学行为的甄别，并约请5位具有丰富教学或科研经验的专家论证了3个角度的权重分布：实践中的使用频率占比0.37，交流中的使用频率占比 0.21，教学上的重要性占比0.42．

每个样本对每个行为的排序可以得到一个三变量数组；计算所有样本对每个行为排序的均值，可以得到16个三变量数组，形成空间直角坐标系中的点阵．在空间直角坐标系中计算各点到点(16, 16, 16)距离，此处距离的取值范围应为．距离 0表明该教学行为具有最高的关键性，是点(1, 1, 1)到点(16, 16, 16)之间的距离，表明该教学行为关键性最低．对距离的计算是在权重分值基础之上的巩固论证．

经计算，得到表4，呈现的是各关键教学行为权重分值以及对应点到点(16, 16, 16)距离．

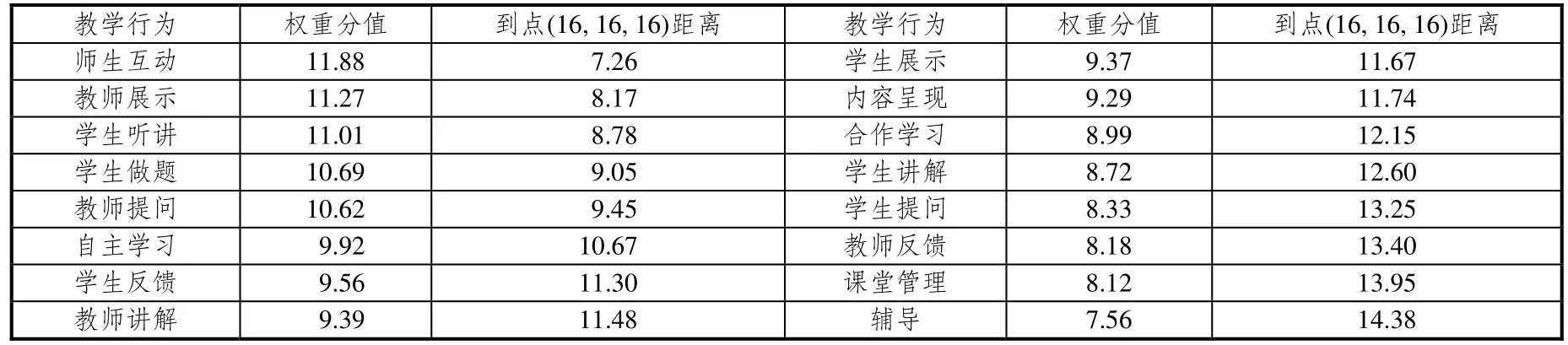
表4 关键教学行为权重分值以及对应点到点(16, 16, 16)距离

4 研究结论与启示

借助 CIT方法，在中学数学课堂教学行为词典项目的基础之上，进一步借助问卷调查以及访谈的方法生成了中学数学课堂教学中关键性最高的5个教学行为：师生互动、教师提问、教师展示、学生听讲以及学生做题．其中，专家论证保证了问卷具有较高的信度、效度，确保所收集的数据能够促进研究问题的解决．

4.1 中学数学课堂教学行为关键性层级分布

通过上述研究过程，对于中学数学课堂教学行为词典项目中的124个教学行为的关键性进行分层研究，依据该教学行为与课堂上其它教学行为之间的关联度建立课堂关联指数CIC，首先将包括布置任务、变式教学、记笔记等在内的8个CIC小于3的教学行为归入C层级．

包括师生互动、教师展示、学生听讲在内的 CIC大于等于3的16个教学行为列为“关键教学行为”，归入A层级和B层级．

通过对16个关键教学行为进一步的问卷调查和访谈，根据16个教学行为的权重分值排序；以及计算其对应点在空间直角坐标系中到点(16, 16, 16)的距离，以这两个角度进一步刻画“关键性”分层，发现权重分值>10，且到点(16, 16, 16)的距离<10的教学行为有5个：师生互动、教师展示、学生听讲、学生做题以及教师提问，将其归入 A层级；包括教师讲解、自主学习、学生反馈、教师反馈、内容呈现、课堂管理、合作学习、学生讲解、学生展示、学生提问、辅导等在内的11个关键教学行为归入B层级．

同时，关键教学行为的提取应更关注教学经验更丰富、教龄更长、职称较高的教师的调查结果．据此，对教龄在10年以上的中一、中高职称教师样本（47个）进行再分析，得到最为关键的5个教学行为分别为：师生互动、教师提问、教师展示、学生听讲以及学生做题，与样本整体获得的 5个关键教学行为一致，仅在排序上微调．综上，将上述 5个教学行为归入A层级，界定为关键教学行为，即CPB．

4.2 中学数学课堂教学行为关键性层级研究意义显著

通过对关键教学行为的鉴别和分层，可知在中学数学课堂教学中，师生互动、教师提问、教师展示、学生听讲以及学生做题具有最为关键的影响力，从促进教学改进，助力学生学习以及教师教学的角度来看，更为关注以上各行为具有一定的积极影响．

结果显示，师生互动具有较高的关键性，既是课堂教学的重要关注，也解释了师生互动何以是许多研究者及一线教师广泛关注的一个话题[13]．

对4名经验丰富的一线教师的访谈也再次论证了A层级教学行为的关键性．学生听讲贯穿课堂教学的始终．教师展示关系到整个课堂的逻辑走向，合理恰当的展示将呈现出知识发生发展的逻辑走向；怎样展示知识内容学生更容易接受，选择什么样的例题，问题环境是怎样的，教师怎么样去引导，通过什么样的方式去展示，这些都是非常重要的．师生互动的重要性也是显而易见的，整个课堂是一个师生进行交流互动的有机整体；教师与学生之间的沟通、互动、思维的碰撞也是很重要的，因此教师在进行课堂教学的时候要充分考虑问题的选择、讲解的方式等能不能营造一个师生互动、交流的平台．对于数学学科而言，学生做题更具有明显的重要性，这一重要性体现在课外的同时，也体现在课堂教学之中：课堂中的练习随时跟踪学生知识习得的程度并暴露存在的问题，为后续教学策略提供支撑．

学生的听讲贯穿课堂的始终，贯穿其它多个教学行为发生发展的过程中，因而其对于整个课堂牵一发动全身的关键性不言而喻．学生听讲与其它教学行为的高度关联体现在多个方面，如：学生听讲过程中教师讲解的方式，听讲过程中伴随的学生的思考以及问题解决，听讲过程中教师的点拨等．要想切实实现学生高质量地课堂听讲，应当注意学生听讲与其它教学行为的高效并发，把学生的学习放在首位，而不是强调被动听讲，被动接受．

4.3 关键教学行为的合力构成高效课堂

关键教学行为并非孤立存在的，而是相互作用，相互关联，共同合力构建出高效课堂．这一结论的依据有两个方面：一是从课堂关联指数可以发现，教学行为之间是密切关联的；二是从对资深特级教师的访谈中可以再证实这一结论．访谈发现，研究探寻从具体的教学情境出发，关键教学行为并非孤立地表现出关键性，其关键性的体现仍有赖于其它教学行为的恰时恰点、合理呈现．

数学教学的国际比较研究正日益受到重视，尤其是对跨文化课堂活动的比较研究[1]．研究基于中学数学课堂教学行为词典项目，该项目中的其他国家课堂教学行为之间也必然存在着关联度以及关键性的分层表现．已有初步探寻可知，差异与共性并存，各国中学数学课堂存在着一定程度的共同关切，同时也存在着不同文化背景下的差别，因而后续研究将对其他国家的中学数学课堂教学行为进行类似层级分布研究，并进行国际比较，对于探寻不同文化背景下的国际中学数学课堂关切具有一定的指导意义[14～21]．

在研究得到的CPB的基础之上，可以进一步结合本国乃至国际课堂，进行跨文化的数学课堂教学比较，探寻CPB在不同文化情境中的表征，并关注教师和学生在CPB过程中的角色定位，对于从关键教学行为入手指导课堂教学改进具有一定的意义．

[1]DavidClarke，曹一鸣，李娜．跨文化数学教学比较研究中的七大困境[J]．数学教育学报，2014，23（4）：13-15．

[2]张昆，曹一鸣．完善数学教师教学行为的实现途径[J]．数学教育学报，2015，24（2）：33-37．

[3]杨玉东，王兄．运用关键性教学事件分析支撑中国式数学课例研究[J]．数学教育学报，2015，24（6）：40-47．

[4]汤立宏．关注关键教育事件，优化教师教育教学行为[J]．中小学管理，2006，（12）：30-32．

[5]沈民冈，汪泠淞．基于“关键教育事件”教师教育的行动研究综述[J]．上海教育科研，2010，（4）：8-11．

[6]Flanagan J C. The Critical Incident Technique [J].The Psychological Bulletin, 1954, 51(4): 327-358.

[7]Tripp D.Critical Incidents in Teaching—Developing Professional Judgement[M]. New York: Routledge Falmer Press, 1993.

[8]Andreou T E. Critical Incidents in Sustaining School-Wide Positive Behavioral [J].Journal of Special Education, 2015, (49): 157-167.

[9]Kanika Aggarwal Khandelwal. Effective Teaching Behaviors in the College Classroom: A Critical Incident Technique from Students’ Perspective [J].International Journal of Teaching and Learning in Higher Education, 2009, 21 (3): 299-309.

[10]Perreault W D. Reliability of Nominal Data Based on Qualitative Judgments [J].Journal of Marketing Research, 1989, 26(5): 135-148.

[11]Holstior.Content Analysis for the Social Sciences and Humanities[M]. Mass: Addison-Wesley, 1969.

[12] 王萍．关键事件技术与主成分分析法在高校图书馆服务质量评价中的应用[J]．情报理论与实践，2012，（12）：79-85．

[13] 曹一鸣，贺晨．初中数学课堂师生互动行为主体类型研究——基于LPS项目课堂录像资料[J]．数学教育学报，2009，18（5）：38-41．

[14] 王光明，廖晶．萨斯喀彻温大学综合规划对中国高校的启示[J]．江苏高教，2014，（3）：154-155．

[15] 王光明．加拿大著名大学的中小学校长培训项目研究及启示[J]．国家教育行政学院学报，2014，（7）：92-95．

[16] 王光明，佘文娟．加拿大教师资格认证与教师评级制度及其启示——以萨斯卡彻温省为例[J]．教育科学，2014，（2）：86-90．

[17] 朱哲民，贾冰．数学探究教学SIRA评价标准建立的尝试[J]．数学教育学报，2016，25（1）：57-60．

[18] 朱长江，李书刚，胡中波．在数学文化课程中引进优质教学资源开展混合式教学的探索与实践[J]．数学教育学报，2016，25（4）：30-32．

[19] 曹一鸣，王万松．高中概率统计内容设置的国际比较——基于15个国家数学课程标准的研究[J]．数学教育学报，2016，25（1）：1-4．

[20] 张玉环，王沛．高中微积分课程国际比较研究——基于十个国家和地区的十四个课标研究[J]．数学教育学报，2016，25（2）：36-43．

[21] 吴立宝．初中数学教材代数内容的国际比较研究[J]．数学教育学报，2016，25（4）：33-36．

Research on the Critical Level of the Critical Pedagogical Behaviors in Middle School Mathematics Classroom

CAO Yi-ming, YU Guo-wen
(Beijing Advanced Innovation Center for Future Education, Beijing 100875, China)

Based on the Lexicon Project, the study focuses on exploring the Critical Pedagogical Behaviors (CPB) in the middle school mathematics classrooms. CIT (Critical Incident Technique) is used and questionnaires and interviews are conducted to further get 16 CPB, in which 5 belong to Level A: Teacher-student-interaction, Teacher questioning, Teacher Presentation, Student listening and Student doing exercising; the other 11 CPB belong to Level B while the other 108 normal pedagogical behaviors belong to Level C.

critical pedagogical behavior; CIT; lexicon project; questionnaire; interview

G632.4

A

1004–9894（2017）01–0001–06

[责任编校：周学智]

2016–11–13

澳大利亚研究委员会（ARC）基金——The Lexicon Project: Analysing pedagogical naming systems from different cultures to reconceptualise classroom practice and advance educational theory（DP140101361）

曹一鸣（1964—），男，江苏南通人，教授，全国数学教育研究会理事长，教育部基础教育专家工作委员会专家，基础教育教材审查委员会专家，主要从事数学课程与教学研究．