基于学业水平质量监测的初中生数学核心素养发展状况调查

董林伟，喻 平

（1．江苏省中小学教学研究室，江苏 南京 210013；2．南京师范大学 课程与教学研究所，江苏 南京 210097）

基于学业水平质量监测的初中生数学核心素养发展状况调查

董林伟1，喻 平2

（1．江苏省中小学教学研究室，江苏 南京 210013；2．南京师范大学 课程与教学研究所，江苏 南京 210097）

依据高中课程标准修订组专家提出的6个数学核心素养，建立三级指标体系对其划分水平，以江苏省2016年中小学生学业质量监测的测试题目为工具，对全省 82 319名初中二年级学生作了测试，将其中涉及数学核心素养的分数作统计．大数据分析表明：（1）江苏省初中二年级学生的6个数学核心素养在总体上达到较高水平；（2）初中学生数学核心素养的发展水平不平衡，在一些核心素养方面两极分化现象比较突出；（3）城乡、不同区域、不同类型学校学生的核心素养水平发展不平衡；（4）数学核心素养水平不存在性别差异．

学业水平监测；数学核心素养；初中学生

1 问题提出

研究基于两个背景．

第一个背景：中小学生学业质量监测．随着2001年课程改革的实施，为了对基础教育质量进行监测，教育部借鉴国际经验于2003年设立了“建立中小学生学业质量测试分析和反馈指导”项目．这个项目从2004年开始，每两年组织一次，在小学三年级和初中二年级进行．江苏省义务教育阶段学生学业质量监测从2006年开始，在教育部项目组的框架中进行．自2014年起，江苏省独立实施义务教育阶段学生学业质量监测，但整体框架和技术标准仍延续原有项目．质量监测与分析在省教育厅的部署下进行，严格依据课程标准，遵循国际上有关教育质量科学测试的要求，并采用9项指数全面体现“质量”内涵．测试范围覆盖全省所有市、县（市、区）．测试后，分别在省、市、县、校四级形成质量分析报告，全面呈现地方和学校课程教学质量情况，对教育教学的过程进行深入细致的诊断，为教育教学和管理改革提供依据．

第二个背景：核心素养的提出．在《教育部关于全面深化课程改革落实立德树人根本任务的意见》中，明确界定了核心素养，即学生应具备的适应终身发展和社会发展需要的必备品格和关键能力．基于这种背景，教育部于2015年开始组织专家对高中课程标准进行修订，要求把学科核心素养作为修订课程标准的主线，围绕学科核心素养制订教学内容、评价标准和教材编制．目前，高中数学课程标准修订组的专家提出了数学核心素养的基本成分：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析，对6种核心素养作了三级水平划分，新的高中数学课程标准即将出台．同时，许多学者对数学核心素养也开展了相关的研究[1～3]．

显然，第一个背景是一种现状，第二背景是一种导向．尽管当下核心素养的提出源于高中课程改革，但是关注发展学生的核心素养是国内外教育改革的必然走向和趋势．面对这种情况，江苏省中小学教研室组织专家对高中数学核心素养的研究作了认真分析，率先把数学核心素养概念引申到初中和小学，参照高中数学课程标准修订组专家对数学核心素养的研究成果并结合《义务教育数学课程标准（2011年版）》（以下简称《标准》），对义务教育阶段数学核心素养作了内涵界定和水平划分．在2016年的全省质量监测的初中数学学科，除了按照原有测试的框架和任务外，把数学核心素养的考察渗透到测试题目中，这是一种从单纯考察知识学习结果到考察知识学习与数学核心素养发展双重功能测试的尝试，同时，通过这次测试希望从中了解当下初中学生数学核心素养发展的基本状况．

2 初中学生数学核心素养解析

2.1 概念界定

《标准》指出；“在数学课程中，应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想．为了适应时代发展对人才培养的需在，数学课程还要特别注重发展学生的应用意识和创新意识．”[4]这个描述指出了初中数学的所谓10个核心概念．将这10个核心概念与高中6个核心素养作对比，数据分析观念与数据分析对应，运算能力与数学运算对应，推理能力与逻辑推理对应，模型思想与数学建模对应．这4个对应前后概念的描述，《标准》与高中课程标准修订组专家的说法内涵基本一致，只是要求和程度上有所差异．

《标准》对于空间观念的界定是：“空间观念主要是指根据物体特征抽象出几何图形，根据几何图形想象出所描述的实际物体；想象出物体的方位和相互之间的位置关系；描述图形的运动和变化；依据语言的描述画出图形等．”几何直观“主要指利用图形描述和分析问题．借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果．几何直观可以帮助学生直观地理解数学，在整个数学学习过程中都发挥着重要作用”[4]．上面的描述中，空间观念有数学抽象成分，思维对象是几何问题，而对几何直观的描述主要说的是它的功能．高中数学核心素养“直观想象”的界定是：“直观想象是指借助空间想象感知事物的形态与变化，利用几何图形理解和解决数学问题．主要包括：利用图形描述数学问题，建立形与数的联系，构建数学问题的直观模型，探索解决问题的思路．”显然，将初中空间观念和几何直观两个概念合并，其内涵与高中的直观想象是基本一致的．

符号意识的涵义是指能够理解并运用符号表示数、数量关系和变化规律，并用符号进行推理，本质上就是一个数学抽象的过程．数感包括对数字关系和数字模式的意识，以及运用这种对数字关系和数字模式的意识灵活地解决数字问题的能力[5]．意识的过程本身有抽象的元素蕴含其中，反映的是人对现实问题中数学要素的抽象．因此，把数感和符号意识合并与高中核心素养中的数学抽象对应．

至于应用意识和创新意识，它们分布于上述各个核心素养要素中．基于上述分析，初中数学核心素养与高中数学核心素养形成一一对应关系，换言之，初中数学核心素养也分为6个要素，简单地描述为：数学抽象是指舍去事物的一切物理属性，得到数学研究对象的思维过程；逻辑推理是指从一些事实和命题出发，依据逻辑规则推出一个命题的思维过程；数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学知识与方法构建模型解决问题的过程；直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用图形理解和解决数学问题的过程；数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的过程；数据分析是指针对研究对象获得相关数据，运用统计方法对数据中的有用信息进行分析和推断，形成知识的过程．

2.2 核心素养的具体表现及水平划分

高中课程标准修订组的专家对 6个数学核心素养作了三级水平划分，这种划分有两个问题，其一，是针对高中数学学习的特征划分的，如果完全搬迁到初中数学学习中来，会有一定的不适应性；其二，3个水平对应的是高中结业、高考、高校自主招生的数学核心素养要求，对于非终结性考试的指导作用不大．有学者以学科核心素养生成的本源是知识为逻辑起点，提出了学科核心素养水平划分为知识理解、知识迁移、知识创新三级水平[6]．因为命题的依据主要来自“学业质量监测”的要求，不完全是依据考察核心素养开展的，因此上面的两种水平划分不适用该研究．

针对初中数学核心素养的特殊性，在作水平划分时要考虑；（1）初中数学核心素养的具体表现及水平应体现初中学生的年龄特点与认知水平．（2）初中数学核心素养不是独立于知识、技能、思想、经验之外的“神秘”概念，它综合体现出对数学知识的理解、对数学技能方法的掌握、对数学思想的感悟及对数学活动经验的积累．（3）数学核心素养的具体表现及水平划分既要参考高中数学核心素养水平划分框架，更要与《标准》所规定的相应的课程内容、目标及要求相适应．

基于这种思考，与高中数学核心素养水平划分的二级指标体系不同，把初中数学核心素养的水平划分为三级指标，一级指标是数学核心素养要素，二级指标是数学核心素养的具体表现，三级指标是每一种表现的水平．具体表现的涵义是把每个核心素养应当达到的目标作出一种分类，这个目标的确定依据《标准》对每一个内容的要求，同时参照高中数学核心素养水平划分的二级指标体系，即将这个二级指标作分类处理．三级指标是对每一种数学核心素养的具体表现作出水平划分，分为A、B、C、D四个水平，A水平最高，D水平最低，一般来说在某一维度处于高水平的学生也能完成较低水平的任务．附录中表1～表6给出了每种核心素养的具体划分描述．

3 试卷设计与被试情况

3.1 试卷设计

由于考试的时间为90分钟，因此测试设计了A、B两套试卷以确保测试内容具有一定的覆盖面．但由于A、B卷的客观难度不可能完全相同，又分别是不同学生群体作答，为保证两卷的等值性，专门设计了S卷，S卷是由从两份试卷中各抽取部分试题组成的，并由第三批学生作答．试卷的题型包括选择题、填空题和解答题，其中A套试卷18题共26小题，B套试卷19题共27小题．测试内容仅限于初一、初二的课程内容．

需要说明的是，由于每一个数学核心素养在发现与提出、分析与解决数学问题和实际问题中，各自在不同的环节发挥不同的作用，而且相互“交着”相互“渗透”，同一个试题可能会涉及多个核心素养的体现．为此，选取该试题重点体现的一个核心素养进行分析统计．具体情况如表1．表1中题目的编号M指数学，8指年级，A代表A卷，B代表B卷，O代表客观题，S代表主观题；后面3个数字前面两个指题号，后面一个指小题号．例如M8AS172指数学8年级A卷的主观题，第17题第2小题．

3.2 数据处理

对于4个水平的分数处理采用Angoff方法．该方法按3个步骤进行[7]：

按照一定的要求选取一组领域评判者，对他们进行培训，使其对于最低能力应试者的概念有较为清楚而统一的看法，并将这组应试者称为边界组考生，他们是达到某一标准最低水平的考生．

要求每一个评判者对于每一个题目做出这样的判断：边界组考生正确回答该题目的概率是多少．

将某个评判者对该测验中所有题目的判断值相加，就是评判者认为边界组考生应当得到的分数．计算所有评判者评分的平均值，就得到合格分数线．

选择一组初中数学特级教师，正高级教师和教研人员，依据这个方法，分别定出优秀水平A、良好水平B、合格水平C、不合格水平D的分数线．

由于采用大样本收集数据，因此对差异性分析没有作统计检验．

3.3 被试选择

表1 涉及数学核心素养的题目分布

表2 被试选择情况

4 测试结果的整体分析

4.1 总体表现

学生在6个核心素养上的各水平表现如图1．

图1 全体学生在数学6个核心素养上的各水平的人数比例

从图1可以看出，初中二年级的学生中有超过90%的学生的核心素养综合表现达到了合格及以上水平，其中有39%的学生达到了A水平．从数学核心素养的6个方面看，学生在逻辑推理、数学建模、数学运算和数据分析等4个方面达到A水平的人数分别达为39%、41%、39%和44%，但在这4个方面处于D水平的人数都超过了10%．学生在数学抽象、直观想象等两个方面达到 A水平的人数虽然只占到学生数的四分之一，但处于D水平的人数只有4%、2%，要明显少于前4个方面．

4.2 不同群体学生的核心素养表现

学生群体按照区域划分为苏南、苏中、苏北，按照城乡划分为城区、镇区、乡村，按照学校性质分为公办、民办，按照性别分为男、女．

从图2可以看出，不同地域的学生在数学核心素养总体表现存在差异，整体上苏中略高于苏南，都明显高于苏北，在逻辑推理、数学建模、数学运算、数据分析等方面优势明显．苏南学生在逻辑推理、数学建模、数学运算、数据分析的A水平的人数比例分别达到42%、45%、43%、48%，但在逻辑推理、数学建模、数学运算和数据分析等4个方面仍处于D水平的人数比例都超过了10%；苏中学生除了数学抽象、直观想象外的 4个方面都有接近半数的学生达到 A水平，但在逻辑推理、数学建模、数学运算、和数据分析等4个方面都有10%左右的学生仍处于D水平；苏北学生在逻辑推理、数学建模、数学运算、数据分析等4个方面也有三分之一的学生达到 A水平，但在逻辑推理、数学建模、直观想象、数据分析等4方面有20%的学生仍处于D水平．

图2 不同地域学生在数学6个核心素养上的各水平人数比例

从图3可以看出，城区初中学生的数学核心素养总体表现都高于镇区学生，且明显高于乡村学生，特别是在数学建模、数据分析等方面优势更加明显．城区学生在逻辑推理、数学运算、数据分析A的高水平的人数比例分别达到43%、 44%、49%，但在逻辑推理、数学建模、数学运算和数据分析等4个方面处于D水平的人数比例都超过了10%；镇区学生除了数学抽象、直观想象外的4个方面都有超过三分之一的学生达到A水平，但在逻辑推理、数学建模、数学运算和数据分析等4个方面都有15%左右的学生处于D水平；乡村学生在逻辑推理、数学建模、数学运算、数据分析等4个方面也有超过四分之一的学生达到A水平，但在逻辑推理、数学建模、直观想象等方面有超过四分之一的学生处于D水平．

评审工作流程更加严密。山东省各级财政评审机构以塑造工作流程为着力点，以防控评审风险为关键点，兼顾质量与效率，多措并举，规范评审程序，提高管理水平，保证评审质量，确保评审工作公平、公正、高效开展。如，枣庄市采取完善评审资料流转程序、制定项目评审预案、完善评审质量保障机制等6项措施，环环严谨相扣，层层压实责任，将监督约束贯穿评审前中后全过程；泰安市按照工作项目化、项目目标化、目标责任化、责任绩效化的“四化”要求，构建一体化评审体系、建立书面质疑清单制度、明确现场踏察规定3条措施，规范工作流程，细分评审步骤，明确职责到人，提高评审质量。

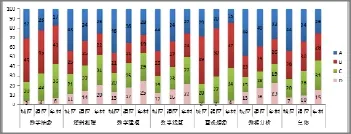
图3 城乡学生在数学6个核心素养上的各水平的人数比例

从图4可以看出，民办初中学校的学生的数学核心素养总体表现明显高于公办，在数学建模、数据分析方面优势更加明显．公办学校学生在逻辑推理、数学运算、数学建模、数据分析等4个方面都有超过三分之一的学生达到A水平，但在逻辑推理、数学建模、数学运算、数据分析等4个方面都有15%左右的学生处于D水平；民办学校学生在逻辑推理、数学建模、数学运算、数据分析等4个方面都有超过半数的学生达到 A水平，但在数学建模、数据分析和数学运算等3个方面有超过5%的学生处于D水平．

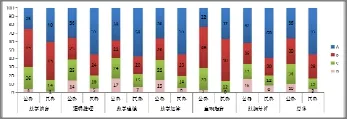
图4 不同性质学校的学生在数学6个核心素养上的各水平人数比例

从图5中可以看出，初中男女学生的数学核心素养总体表现上没有差异，都有接近40%的学生达到A水平，处于D水平的人数都低于10%，但在数学建模、数据分析、逻辑推理、数学运算等4个方面都有15%左右的学生仍处于D水平．

图5 不同性别学生在数学6个核心素养上各水平人数比例

4 讨 论

这次作的大数据测试，尽管测试标准是按照学业水平质量监测拟定的，不是严格意义上对学生核心素养发展的全面检测，但尝试在测试题目中加入了测量数学核心素养的要素，得到的数据在一定程度上反映了江苏省初中二年级学生数学核心素养的基本状况．

首先，从整体情况看，江苏省初中二年级学生的6个核心素养达到了比较高的水平，在 A水平层面，逻辑推理、数学建模、数学运算、数据分析表现更好，但也正是这 4个方面，D水平的百分比较大，因而这4个因素的发展水平分化现象更加突出．数学抽象和直观想象的B水平人数多，D水平的人数最少，反映了这两个要素的集中趋势．产生这种现象的原因可能是由于数学建模与数据分析对初二年级学生而言是一个比较新的内容，思维方式发生了变化，使许多其他素养不高的学生不能适应，而其他素养高的学生会很快适应，于是产生了分化现象．

其次，从不同群体的数据反映出在总体方面，苏中地区学生的数学核心素养形成水平略高于苏南地区，苏中与苏南都明显高于苏北，体现出一定的地区差异．3个地区在数学建模和数据分析方面处于 D水平的比率较大，两极分化现象比较突出．从不同类型的学校看，城区初中学生的数学核心素养总体表现都高于镇区学生，且明显高于乡村学生，特别是在数学建模、数据分析等方面优势更加明显．这个结果反映出城乡之间存在差异，折射出教育发展的不均衡性．从性别差异看，男女生在6个核心素养方面不存在差异．

5 结 论

（1）江苏省初中二年级学生的6个数学核心素养在总体上达到较高水平，其中在逻辑推理、数学建模、数学运算、数据分析等4个要素上达到A水平的比率更大．

（2）初中学生数学核心素养的发展水平不平衡，特别逻辑推理、数学建模、数学运算、数据分析等4个要素方面两极分化现象比较突出．

（3）不同区域、不同类型学校学生的核心素养水平发展不平衡，苏中地区略高于苏南地区，苏中与苏南都明显高于苏北；城区总体表现都高于镇区，且明显高于乡村；民办学校总体表现明显高于公办学校．

（4）男生与女生的数学核心素养水平不存在显著差异．

[1]郑毓信．数学教育视角下的“核心素养”[J]．数学教育学报，2016，25（3）：1．

[2]喻平．数学学科核心素养要素析取的实证研究[J]．数学教育学报，2016，25（6）：1．

[3]王光明，张楠，周九诗．高中生数学素养的操作定义[J]．课程·教材·教法，2016，（7）：50．

[4]中华人民共和国教育部．义务阶段数学课程标准[M]．北京：北京师范大学出版社，2011．

[5]徐文彬，喻平．“数感”及其形成与发展[J]．数学教育学报，2007，16（2）：8．

[6]喻平．发展学生学科核心素养的教学目标与策略[J]．课程·教材·教法，2017，（1）：48．

[7]余嘉元．Angoff方法有效性的检验研究[J]．教育研究与实验，2008，（1）：54．

附录：核心素养的具体划分描述

表1 数学抽象的具体表现与表现水平

表1 （续） 数学抽象的具体表现与表现水平

表2 逻辑推理的具体表现与表现水平

表3 数学建模的具体表现与表现水平

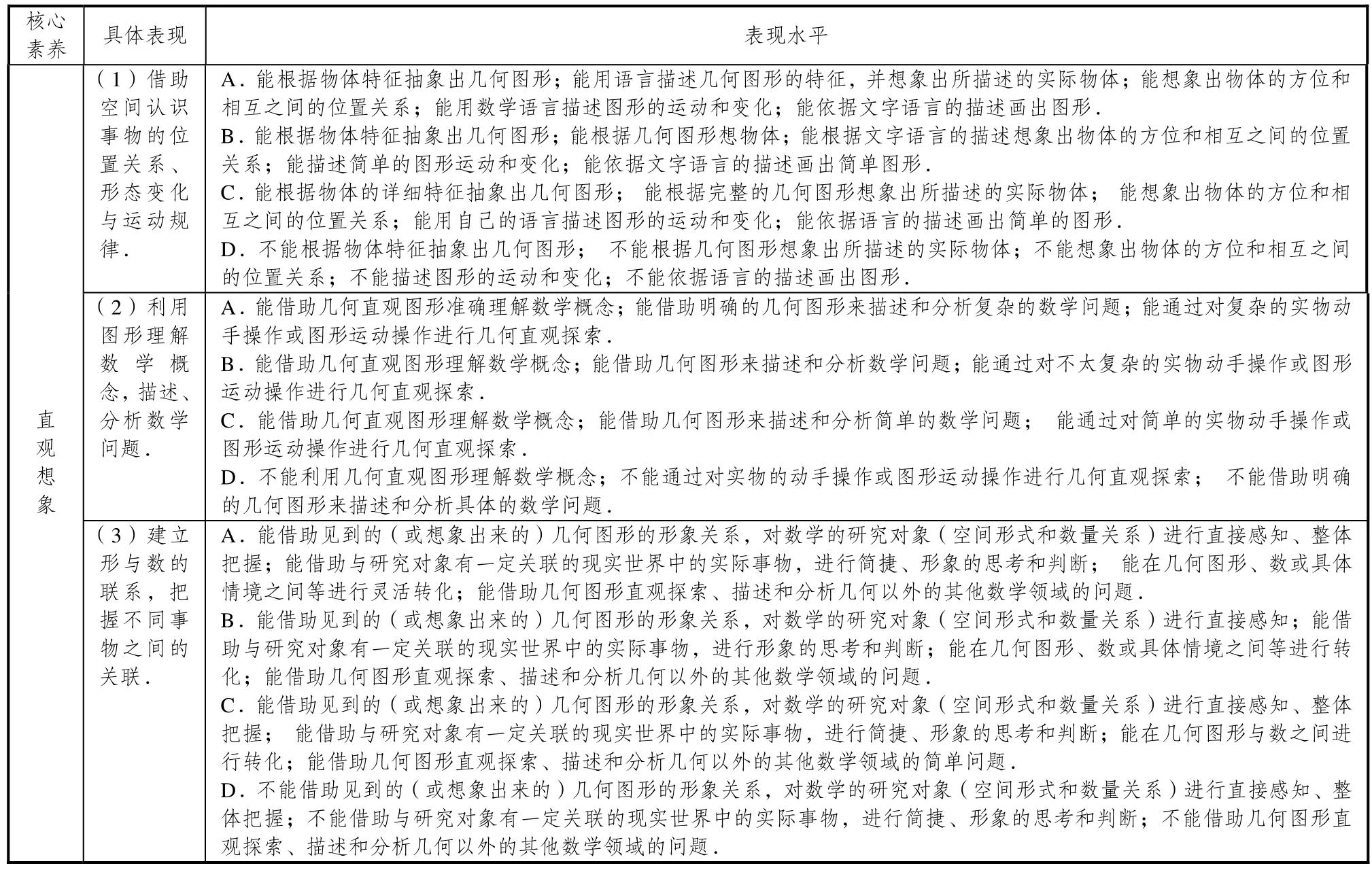
表4 直观想象的具体表现与表现水平

表5 数学运算的具体表现与表现水平

表6 数据分析的具体表现与表现水平

[责任编校：周学智]

Investigation on the Development of Mathematical Key Competencies of Junior High School Students Based on the Academic Level Monitoring

DONG Lin-wei1, YU Ping2
(1. Teaching Research Office Jiangsu Provincial Department of Education, Jiangsu Nanjing 210013, China; 2. Research Institute of Curriculum and Teaching, Nanjing Normal University, Jiangsu Nanjing 210097, China)

Three-level index system is established based on the six math key competencies which revised by senior high school curriculum standard revisionists. 82 319 Grade 8th students in Jiangsu Province are tested by using items from the 2016 Jiangsu Primary and Middle School Students Academic Level Monitoring Test, and their math key competencies scores are analyzed in detail. The big data analysis shows that: (1) The six math key competencies of 8th grade students in Jiangsu province have achieved overall higher levels; (2) Their math key competencies level is unbalanced and polarized in some aspects. (3) The math key competencies of high school students is uneven developed and there is polarization exists among different schools and regions. (4) No gender difference was found in the level of math key competencies.

academic level monitoring; mathematics key competencies; junior high school students

G632

A

1004–9894（2017）01–0007–07

2017–01–20

江苏省教育厅基于测试分析的跟进式改革重大研究项目——义务教育学科核心素养和关键能力研究（2015JYKTZD-02）；江苏省中小学教学研究第十一期重点课题——初中数学学业水平评价研究（2015JK11-Z085）；江苏省社科基金——中小学生数学核心素养体系建构与教学实践研究（15JYD001）

董林伟（1965—），男，江苏宜兴人，特级教师，教授级高级教师，主要从事数学教育研究．