基于“直观想象”数学核心素养的解题策略
——以浙江省2016年高考理科第19题为例
2017-04-24吕增锋邮编315731
吕增锋 (邮编:315731)
浙江省象山县第二中学
基于“直观想象”数学核心素养的解题策略
——以浙江省2016年高考理科第19题为例
吕增锋 (邮编:315731)
浙江省象山县第二中学
直观想象是高中数学六大核心素养之一,其指借助几何直观和空间想象感知事物的形态与变化,利用图形理解和解决数学问题的过程.直观想象是发现和提出数学问题、分析和解决数学问题的重要手段,是探索和形成论证思路、进行逻辑推理、构建抽象结构的思维基础.在数学解题中,直观想象更是不可或缺的重要思维与工具.很多看似复杂,无从下手的数学问题,借助直观想象就可能很容易获得解题的捷径.下面以浙江省2016年高考理科第19题为例,谈谈对此的看法.
(I)求直线y=kx+1被椭圆截得的线段长(用a、k表示);
(II)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围.
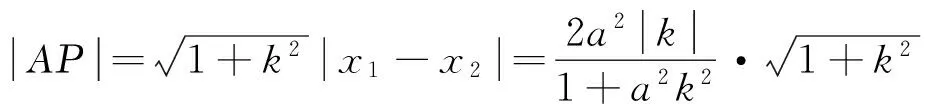
直接解法
设动圆的半径为r,则动圆与椭圆的交点个数就转化为方程根的个数.
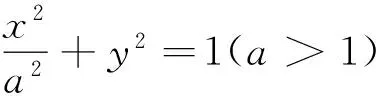
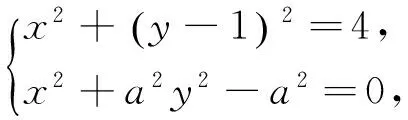
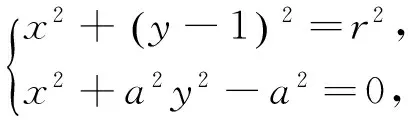
②
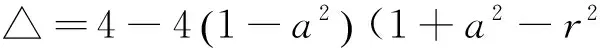
(i)f(y)=0的唯一解位于区间[-1,1]上,此时圆与椭圆最多有2个交点.
(ii)f(y)=0的唯一解不在区间[-1,1]上,此时圆与椭圆无交点.
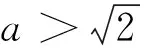
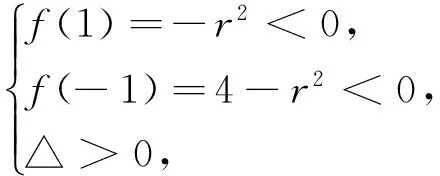
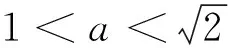
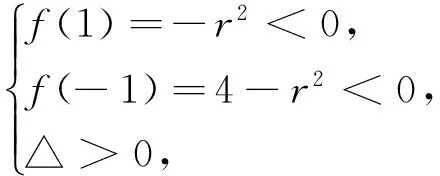
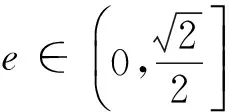
1 利用图形描述,理解问题本质
导致解题过程繁琐的很大一部分原因是对“题意”的理解不够透彻,没有深入到问题的本质.当题目呈现的关系比较复杂时就很难从字面上直接获得解题的线索,这时如果借助“图形描述”手段,即把“自然语言”转化为“图形语言”就容易找到问题的突破口.“图形描述”可以是学生动手作图,也可以是教师通过计算机软件演示.
对于上述题目来说,解题的关键是要搞清楚“圆的半径”、“交点个数”、“离心率”三者之间的联系.过A点作一系列半径大小不一的圆,发现圆与椭圆交点的个数有0、1、2、3、4等五种情况,而且交点的个数除了与圆的半径大小有关外,还与椭圆的圆扁程度相关,而离心率的大小决定了椭圆的圆扁程度,这就明确了条件与结论之间的联系.再类比问题(I),发现直线y=kx+1恰好经过定点A,AP就是圆与椭圆的一条相交弦.连结点A与交点,就得到一条相交弦;有几个交点便有几条等长的相交弦,交点问题就转化为弦长问题.至此,本题的解题思路就清晰起来了.
优化解法1
先考虑与椭圆有4个交点的情景,然后排除这种情景,就可以得到符合条件的结论.
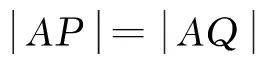
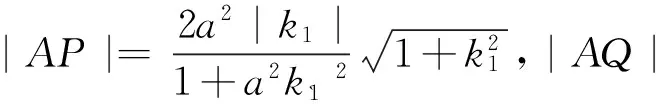
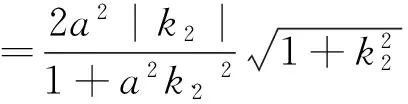
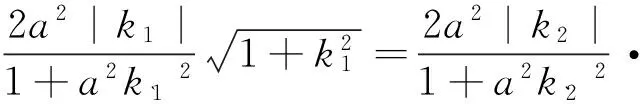
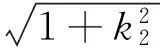
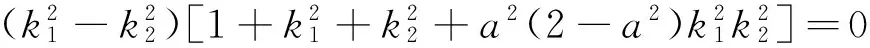
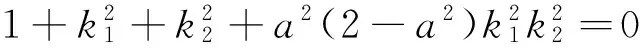
2 挖掘几何意义,建立数形联系
数与形是一种特殊的对立,在一定条件下可以实现相互转化.数量关系获得几何解释,可以使问题变得直观易懂,使人易于洞察问题的本质.几何问题得到代数表示,可以使几何直觉,合情推理等转化为程序化操作的代数运算,实现化难为易的目的,并使人获得对问题的精确化、理性化的理解.
优化解法2
假设圆与椭圆的公共点有4个交点,则|AP|=|AQ|,则在椭圆的两侧各存在一个等腰三角形.这样就把“线段长度相等”的代数关系,转化为存在“等腰三角形”的几何关系,然后根据“等腰三角形底边中点”的位置关系列式求解.
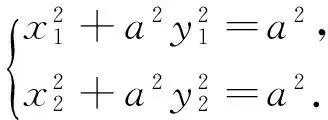
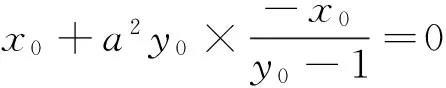
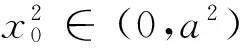
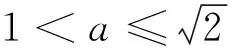
3 运用动态想象,揭示运动规律
学生在视、知觉上表现出的最大障碍,可能就是不能有效地建立视、知觉符号和大脑中储存的图式或概念之间的联系,而动态想象是形成学生知觉形体特征的重要手段.动态想象不仅包含着图形的变化,更蕴含着数学思考.按照皮亚杰的研究,动态表象是学生数理逻辑经验生成的源泉,静态表象只能产生物理经验.动态想象是直观想象的翅膀,在数学解题中,运用动态想象,可以实现由被动感知到主动再现、由单一角度到多种角度来感知运动当中的不变量.
首先,若把题目中的椭圆看成圆,众所周知圆与圆最多有两个交点.由此我们得到启示:椭圆越接近于圆,越不会出现超过3个交点的情况,因此,椭圆的离心率越小越好.
其次,相交弦AP的长度是在变化的,易知其在椭圆上的某个位置取到最大值,只有当AP取到最大值的位置在椭圆短轴的下端点时才不会出现4个交点的情景,因此,从弦长最值出发,这道题的解答过程就会简洁得多.
优化解法3
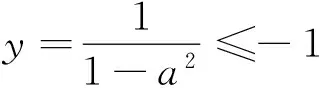
4 深入问题源头,获得直观模型
解题并不是以获得正确答案为最终目的,而是通过经历一道题的解决过程,发现解题规律,揭示本质,从而获得一类题的解题思想与方法.正如华罗庚先生所言:“数学是一个原则,无数内容,一种方法,到处可用.”因此,解题并不能仅停留在题目的表面,而是要深入其内部,找到问题的源头,进而获得直观模型.
原题 若以原点为圆心,椭圆的半焦距长c为半径的圆与该椭圆有四个交点,则该椭圆的离心率的取值范围为______.
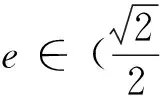
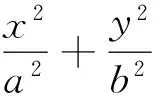
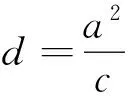
②当b>c时,直线被椭圆截得的最大弦长为d=2b,即为短轴长.
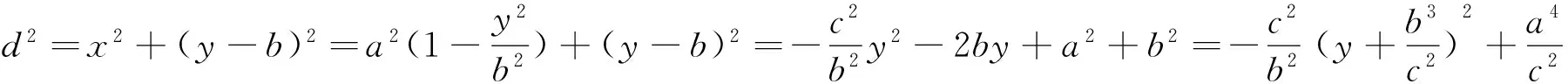
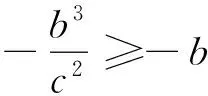
若在解题中,直接从这个“模型”入手,学生就很容易理解“交点个数”与“离心率”之间的关系,容易获得“b>c”的结论,进而直接写出离心率的取值范围.
直观想象是对于数学对象的全貌和本质进行的直接把握,这种直接判断建立在针对几何图形长期有效的观察和思考的基础之上,既有相对丰富的经验积累,也有经验基础之上的理性的概括和升华.因此,运用直观想象开展数学解题活动需要平时不断地潜移默化,积累经验,最终实现运用自如的目的.
2016-12-28)
