巧用平面几何知识证明圆锥曲线的一条统一性质

郑观宝 (邮编：245200)

安徽省歙县中学

巧用平面几何知识证明圆锥曲线的一条统一性质

郑观宝 (邮编：245200)

安徽省歙县中学

众所周知，圆锥曲线的光学性质本质上就是圆锥曲线的平面几何性质.为方便读者，下面给出圆锥曲线的光学性质和矩形的两条简单性质．

1 圆锥曲线的光学性质与矩形的性质

(1)在抛物线中，从焦点F发出的光线，经抛物线反射，反射光线一定平行于对称轴(如图1)；

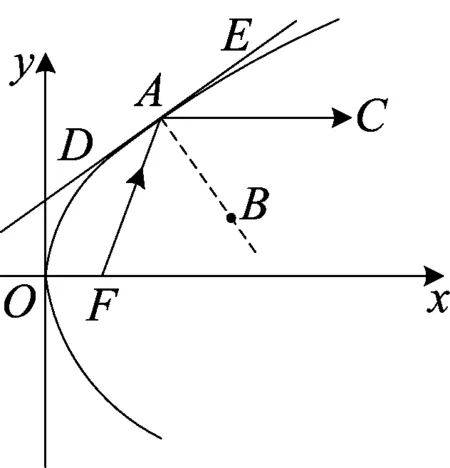
图1

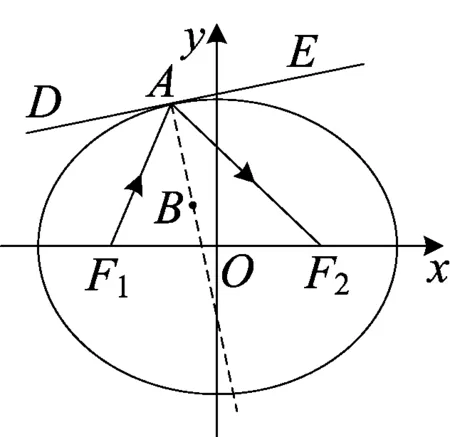
图2

由光线的反射原理可知，光线在点A的反射遵循平面镜反射原理，抛物线在该点的切线就是平面镜，所以，入射角∠FAB=反射角∠CAB，所以它们的余角也相等，即∠FAD=∠CAE，于是得到下列推论：

推论1 在图1中，过点A作该抛物线的切线，以及切线的垂线，则有∠FAD=∠CAE,∠FAB=∠CAB.

(2)在椭圆中，从焦点F1发出的光线，经椭圆反射，反射光线一定经过另一焦点F2(如图2)；

推论2 在图2中，过点A作该椭圆的切线，和切线的垂线，则有∠F1AB=∠F2AB,∠F1AD=∠F2AE．

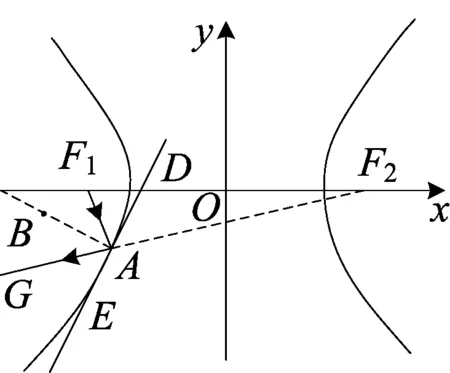
图3

(3)在双曲线中，从焦点F1发出的光线，经双曲线反射，反射光线的反向延长线必经过另一焦点F2(如图3)；

推论3 在图3中，过点A作该双曲线的切线，和切线的垂线，则有∠F1AB=∠GAB,∠F1AD=∠GAE．

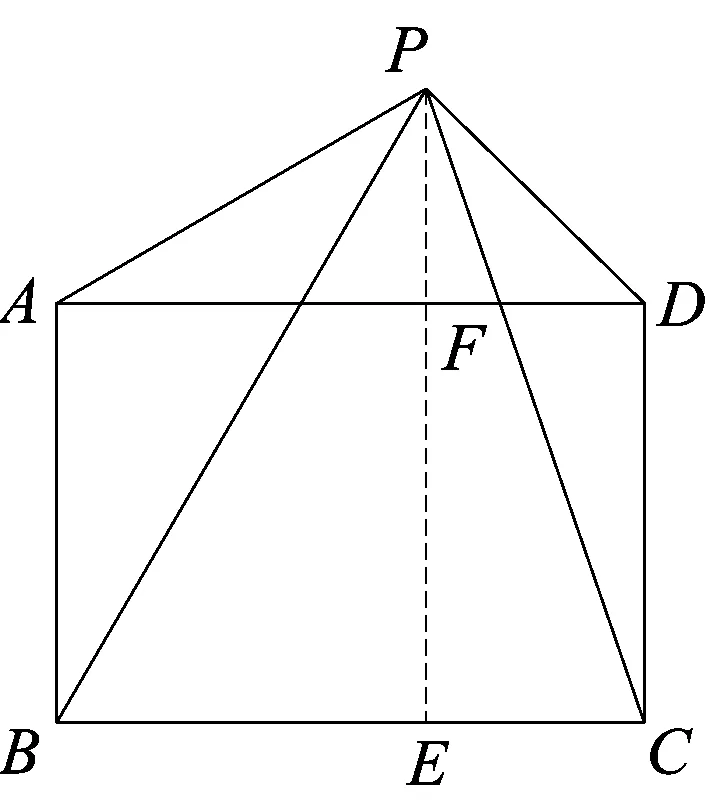
(4)矩形的性质1：矩形ABCD所在平面内任意一点P在相对两个顶点的距离平方和相等，即PA2+PC2=PB2+PD2.

简证 过点P作直线AD、BC的垂线，垂足分别为E、F．由勾股定理可得：PA2-PD2=AF2-DF2，PB2-PC2=BE2-CE2.

又因BE=AF,CE=DF，故PA2-PD2=PB2-PC2，故PA2+PC2=PB2+PD2.

矩形的性质2 矩形ABCD的顶点B、D到其对角线AC的距离相等．

2 椭圆的两条相互垂直的切线的交点的轨迹是什么

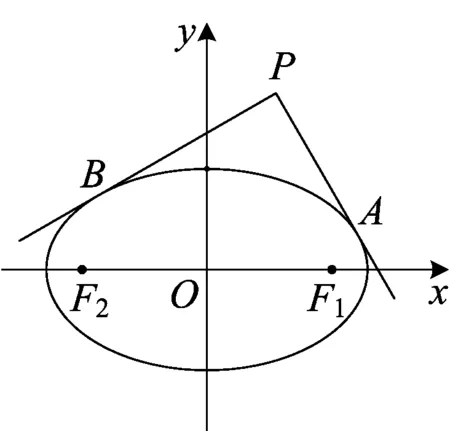
文1 用代数的方法给出了证明，为了方便读者阅读，现将主要过程重述如下：

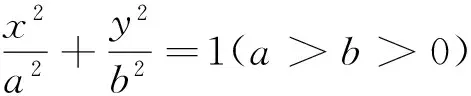
由△=[2a2(v-ku)k]2-4(b2+a2k2)·[a2(v-ku)2-a2b2]=0，化简得(a2-u2)k2+2uvk+b2-v2=0，

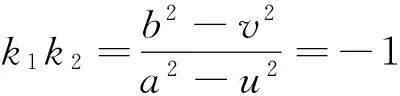
故u2+v2=a2+b2，即两切线的交点P的轨迹为圆x2+y2=a2+b2.

事实上，还有下列解代数解法.

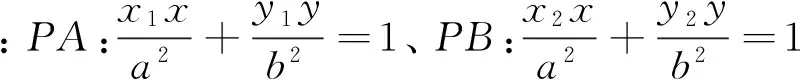
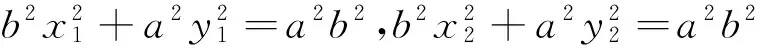
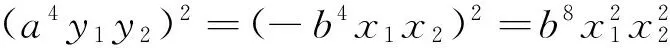
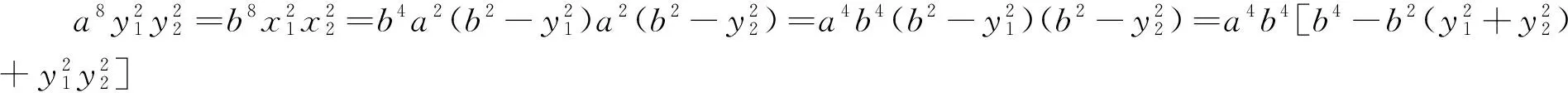
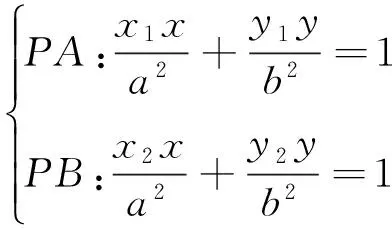
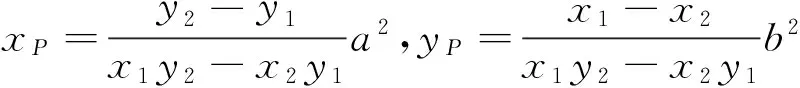
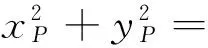
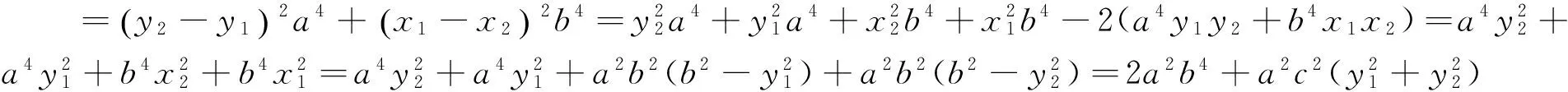
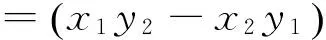
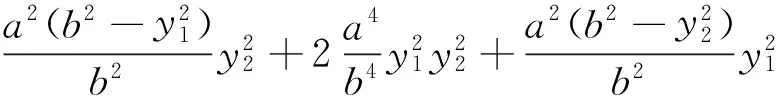
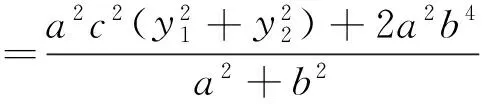
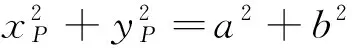
从上述两种方法可以看出，代数法计算量特别大，过程十分繁琐，大部分学生都只是“会而不对”，几乎不可能独立、正确完成．那么还有其他证明方法吗？回答是肯定的，就是利用“椭圆的光学性质和平面几何知识”．

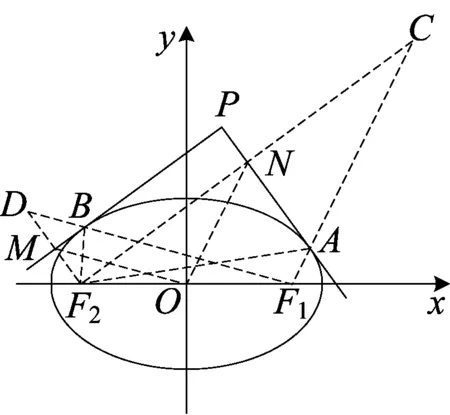
解法3 如图，作焦点F2关于切线PA、PB的对称点C、D．

(1)连接BD、BF1、BF2，由椭圆的光学性质可得：∠MBF2=

∠PBF1，又∠MBF2=∠MBD，

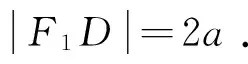
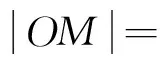
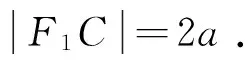
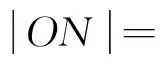
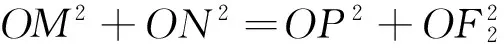
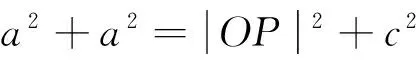
3 圆锥曲线的同一性质——圆锥曲线的两条相互垂直的切线的交点的轨迹是一个定圆

上述解法3能推广到双曲线和抛物线上吗？

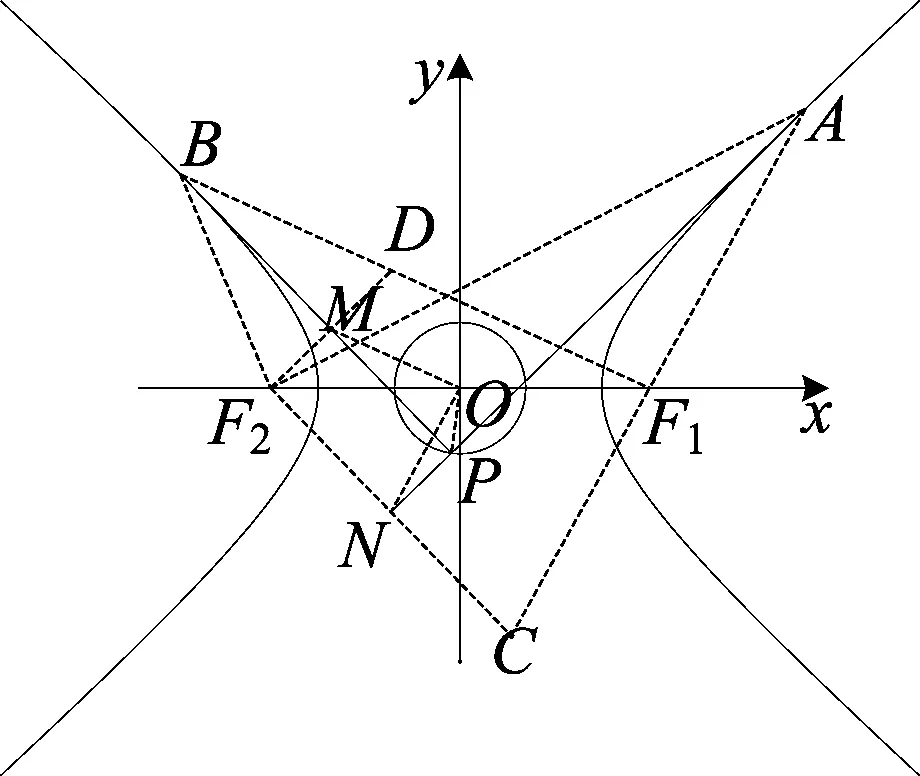
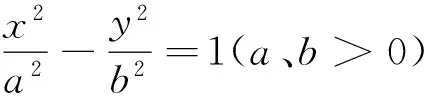
证明 如图，作焦点F2关于切线PA、PB的对称点C、D．

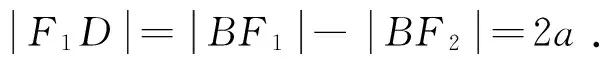
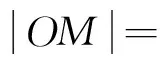
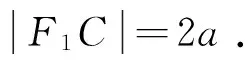
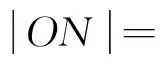
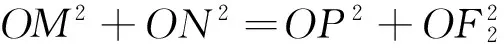
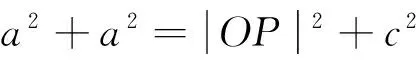
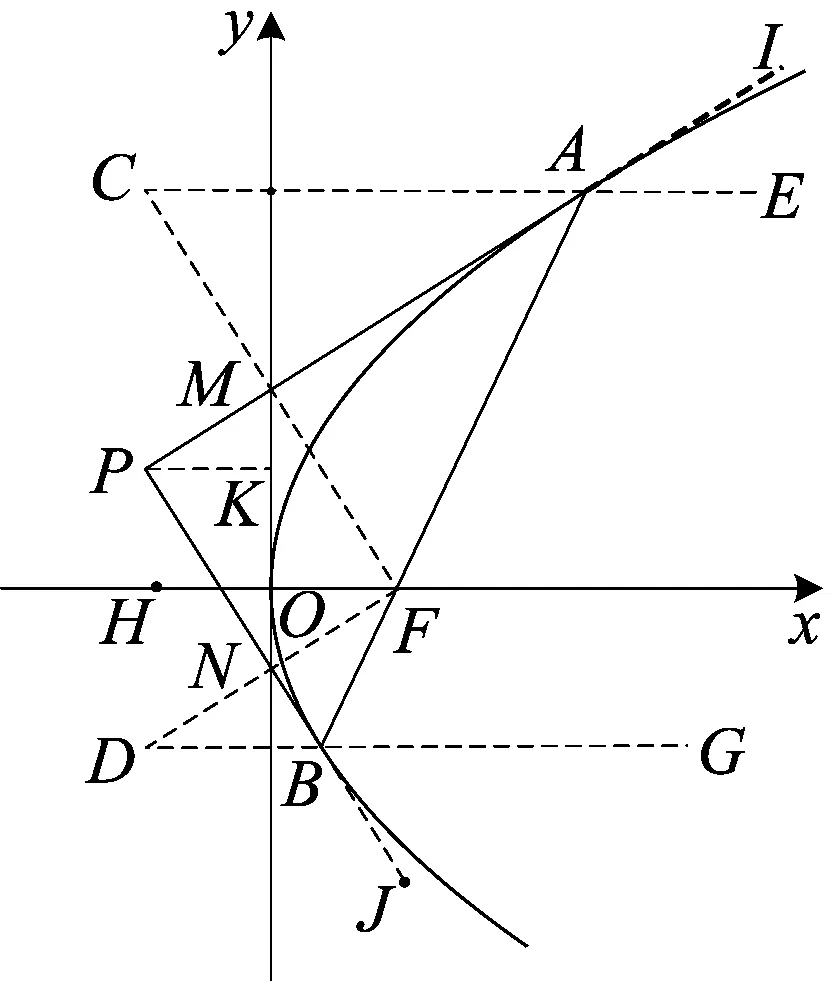
性质3 已知抛物线y2=2px(p>0)，过点P作抛物线的两条切线PA、PB(A、B为切点)，设F为抛物线的焦点．若PA⊥PB，则点P的轨迹为其准线．

证明 如图，作焦点F关于切线PA、PB的对称点C、D．

(1)连接BD、BF，则∠NBF=∠NBD，

过B作y轴的垂线BG，由抛物线的光学性质得∠NBF=∠GBJ，所以∠NBD=∠GBJ，故D、B、G三点共线，所以BD与准线垂直，又BD=BF，所以点D在准线上，则DF的中点N在y轴上．

(2)同理可得AC与准线垂直，点C在准线上，且CF的中点M在y轴上．

(3)由(1)、(2)以及PA⊥PB可得四边形PMFN为矩形，由矩形性质2可得点P、F到对角线MN的距离相等，即PK=OF，故点P的轨迹方程为准线．

如果将直线看作是“半径为无穷大的圆”、抛物线看作“中心在无穷远处的有心圆锥曲线”，那么我们就得到：

圆锥曲线的统一性质 圆锥曲线的两条相互垂直的切线的垂足的轨迹是一个以其中心为圆心、半径为定值的定圆．

1 郑观宝.“情侣圆锥曲线”及其简单性质[J].中学教研(数学)，2006(9)

2017-12-31)