诗意课堂 醉美数学——兼谈文化素养下的数学课堂教学

蒋满林 (邮编：352200)

福建省古田县第一中学

诗意课堂 醉美数学
——兼谈文化素养下的数学课堂教学

蒋满林 (邮编：352200)

福建省古田县第一中学

数学是人类文化的重要组成部分，数学课程应提倡体现数学的文化价值，数学教学不应只看作知识的传授，更应当作一种文化的传承，理性价值观的传递，艺术美的传导，真善美的传播．

文化;数学;课堂教学

课程标准基本理念强调：数学是人类文化的重要组成部分，数学课程应提倡体现数学的文化价值．克莱因在《西方文化中的数学》中说到：“数学不仅是打开科学大门的钥匙，一种科学语言，一门知识体系，一种技术工具，一种独特的思维模式，而且充满理性精神，是一种思想方法、一种具有审美特征的艺术，一种充满人类创造力和想象力的文化境界和一幅饱含人类理想和夙愿的世界图式．” 同时2017年高考数学考纲新增了数学文化的考查，因此，数学教学不应只看作知识的传授，更应当作一种文化的传承，理性价值观的传递，艺术美的传导，真善美的传播．从而在数学课堂教学中应从以人为本的文化视角下进行教学．下面结合教学实例谈谈文化素养下的数学课堂教学．

1 教学实例

案例1 “负负得正”——小城故事多

用故事的形式进行教学，无疑会激起学生的更多兴趣和热情，而优美的故事往往会给他们留下终身的印象，而对真善美的追求更是我们教育的天职，下面讲述这样一个故事．

好人记作+，坏人记作-，进城记作+，出城记作-

好人(+)进城(+)，对于城里来说是变好(因为城里好人变多)，所以：(+)×(+)=+

好人(+)出城(-)，对于城里来说是变坏(因为城里好人变少)，所以：(+)×(-)=-

坏人(-)进城(+)，对于城里来说是变坏(因为城里坏人变多)，所以：(-)×(+)=-

坏人(-)出城(-)，对于城里来说是变好(因为城里坏人变少)，所以：(-)×(-)=+

现代数学教学观认为：学生知识的建构并不是通过演绎推理，而是通过经验收集、比较结果、一般化等手段来完成的，仅仅向学生讲述运算不能收到你所期望的效果，因为学生并不情愿利用这些运算律，这已被现实教育所证实．无疑现实模型(甚至故事模型)是引领教学走向成熟的重要组成部分．

案例2 颜值函数——中华老字号

对于高中数学中颜值很高，出镜频频的函数图象进行塑形标名(见下页图1)．

这些函数包括了单调与周期、连续与间断、无穷与渐近、分段与分类、奇偶与对称、极值与最值等函数最主要的性质．

心理学研究表明：人的记忆不是线状，而是片状记忆，如果数学信息能用图表的方式呈现，则更有利于学生的记忆与理解，这样也为数学文化的传播提供了一种有利的语言——图表信息．

案例3 “e”的记忆——老顽童扒油漆e=2.718281828459045……

中学里有两个经典的无理数π和e，其中的π可以说无人不晓无人不知，甚至有很多人能背圆周率(π的近似值)上百位，而对于e的记忆却相当的模糊，这与圆周率的文化故事传播有一定的关系，其实e的记忆也有很有趣的故事．

y=x[]步步高函数y=x{} 棒棒糖函数y=1x-1囧函数y=x2+1x对勾函数y=xx2+1海鸥函数y=ax2+2x+1 分类函数

图1

刷油漆高手老顽童，一天在刷油漆，身上一不少心沾上两点漆(2.7)，为了把油漆弄下来，他一扒两扒(1828)，但是还没有弄下来，于是再一扒两扒(1828)，而且一边扒一边自言自语：“失误(45)！我久练(90)也失误(45)了！

笔者在历届的教学中都会讲到这个故事，效果出奇的好，学生毕业多年以后，一说起e还念念不忘．数学中有些问题(很多数学名题正是因为它很难发现或很难证明而出名的，如勾股定理、韦达定理、多面体的欧拉公式等)的教学策略，应该与语文、历史等人文学科一样，引导学生进行欣赏，让学生带着愉悦的心情在课堂上学习．因此，数学中的一些问题不是用来证明的，而是用来营造情境让人身心愉悦．

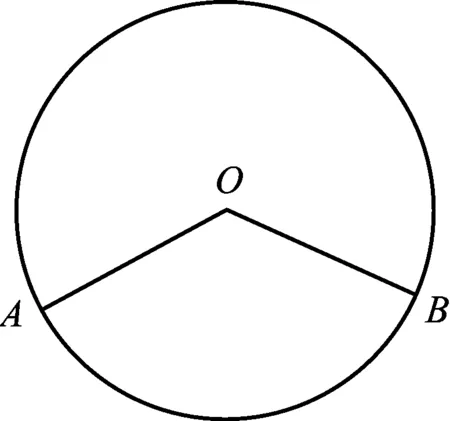
图2

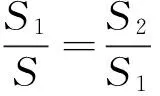
图3

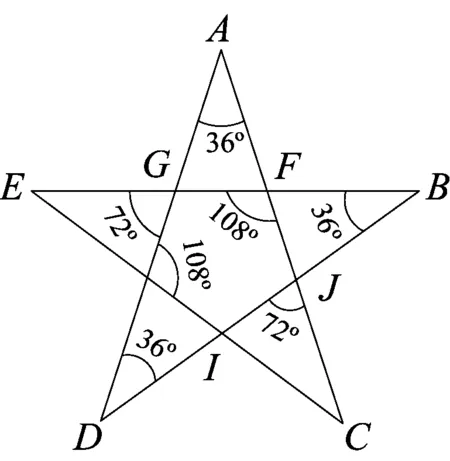
图4

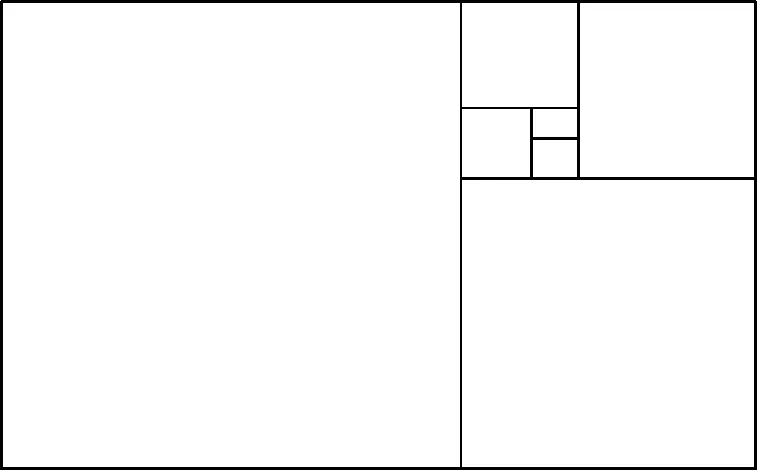
图5

黄金矩形如图4(GoldenRectangle)，黄金矩形的长宽之比为黄金分割率，换言之，矩形的短边为长边的 0.618倍．黄金分割率和黄金矩形能够给画面带来美感，令人愉悦．在很多艺术品以及大自然中都能找到它，希腊雅典的巴特农神庙就是一个很好的例子．达芬奇的脸符合黄金矩形，同样也应用了该比例布局.

黄金分割已被美学界称为美的信条，正如数学家帕乔里所说“一切企图成为美的世俗物，都得服从黄金分割．”因此在数学教学活动中，应挖掘教学素材中的美的因素，并把它引入到课堂教学中，让学生在美的熏陶中，打开心智，在心动情生中激发学习数学的兴趣，从而提高教学效率．

案例5 文以载数——诗词大会

数学不应只看作是一知识，更应理解为是一种文化，一种可以与中华文化经典融合的文化，在数学课堂教学中，积极建构人文意境，对落实情感态度价值观不愧为一种可行有效的方法．下面三题分别是文化数学、数学概念与中华文化经典、数学与文学的自然对接．

题目1

1.下列选项中，与其他三个选项所蕴含的数学推理不同的是( B )

A．独脚难行，孤掌难鸣

B．前人载树，后人乘凉

C．物以类聚，人以群分

D．飘风不终朝，骤雨不终日

2.“红豆生南国,春来发几枝.愿君多采撷,此物最相思.”这是唐代诗人王维的《相思》诗,在这4句诗中,哪句可作为命题( A )

A.红豆生南国 B.春来发几枝

C.愿君多采撷 D.此物最相思

题目2 (填中华文化经典)

圆(《墨子》一中同长)；极限(李白《黄鹤楼送孟浩然之广陵》孤帆远影碧空尽或《庄子》一尺之棰，日取其半，万世不竭．)；数学归纳法(《道德经》：三生万物或道生一，一生二，二生三，三生万物．)；反证法(苏试《琴诗》：若言琴上有琴声，放在匣中何不鸣？若言声在指头上，何不于君指上听？)；存在性命题或抽屉原理(贾岛《寻隐者不遇》松下问童子，言师采药去，只在此山中，云深不知处．)等等．

题目3 (写感悟与认识)

(1+0.01)365≈37.8, (1-0.01)365≈0.03 (此为笔者班训，只有数字没有文字)．

勤学如春起之苗，不见其长，日有所增；辍学如磨刀之石，不见其损，日有所亏．

(注：此语为陶渊明先生赠送后生当勤学苦练的座佑铭)

在课堂教学实践中，受到了学生高度欢迎，激发了学生学习数学的热情，改变了对数学冷俊、严谨、枯燥的印象，教学效率事半功倍，对课程理念落实“立德树人”“文化育人”有了切身的感受与认识．

2 几点思考

2.1 诗意课堂的“诗”境

(1)学起来，有趣:在问题情境建构中，可以融合故事、诗歌、谜语等文学方式，让学生感到学习数学有趣、有味，继而因趣而学数学，因趣而乐数学．

(2)学之后，有益:在课后应安排学生数学写作，让学生写学习后的反思、写对数学概念的理解、对解题方法的体会、写数学学习的感悟等，从而使学生因数学写作而完善思维品质，因数学写作而收获精彩人生．

数学家克莱因说“音乐能激发或抚慰情怀，绘画能使人赏心悦目，诗歌能动人心弦，哲学使人获得智慧，科技可以改善物质生活，但数学却能提供以上一切．” 情到意时诗最美，意到画时情最真，因此数学教学的价值取向不应定位成方法与规则，更应是一种思想、一段历史，从而提升学生的数学文化素养，体现数学教学是“数学文化背景下的思维活动”．

2.2 诗意课堂的“思”性

(1)数学教学需要磁性：数学教师要把冰冷的教材知识，经过巧妙的演绎转化为火热的课堂教学，要象磁一样吸引学生引人入胜，其中文化视角给我们指明了一条途径．

(2)数学教学需要理性：数学是一门理性严谨的科学，在让学生热情起来积极投入课堂教学时，还需让学生沉下来进行理性思考学习，情感调动只是数学教学的手段，理性学习才是数学教学的着眼点．

(3)数学教学需要诗性：数学教学不应只是传授知识，更应看作是一种文化交流，一种火热的诗歌，以简洁的语言、精巧的结构、严谨的思维，给人启迪催人奋进！

数学教育家齐友民说“历史已经证明，一种没有相当发达的数学的文化是注定要衰落的，一个不掌握数学作为一种文化的民族也是注定要衰落的．”可见文化素养不仅是数学课堂教学的需要，更是数学教育的需要．同时新标准强调：教学过程要注重学生的情感态度价值观．教育家第斯多惠说过：“我们认为教学的艺术不在于传授的本领，而在于激励、唤醒、鼓舞，而没有兴奋的情绪怎么能激动人，没有主动性怎么能唤醒沉睡的人，没有生气勃勃的精神怎么鼓舞人呢？”因此，数学教学还应具有激发学生情感的功效．当教师入境入情时，带动了学生的心动情发，师生的情感产生了心灵共鸣，当师生的心灵最接近时，就是课堂教学效率最高之时．教学是一门遗憾的艺术，诗意课堂，醉美数学也许是一图愿景，虽不能至，心往向之.

1 严士健，张奠宙，王尚志．普通高中课程标准(实验)解读[M].南京：江苏教育出版社

2 张奠宙．数学欣赏：一片等待开发的沃土[J].中学数学教学参考，2014(1-2)：3-6

3 蒋满林．数学新课堂教学探索[J].数学教学通讯，2009(3)：6-7

本文系福建省教育科学“十三五”规划2016年度立项课题“‘核心素养’理念下的数学变式教学的行动研究”(立项批准号MJYKT2016-178)的阶段成果.

2017-01-20)