经历概念形成过程 促进学生有效理解——以“一元二次方程”教学为例

张 森 (邮编：235100)赵 彪 (邮编:236000)

安徽省淮北市濉溪城关中心校 安徽省阜阳市北城小学

经历概念形成过程 促进学生有效理解
——以“一元二次方程”教学为例

张 森 (邮编：235100)赵 彪 (邮编:236000)

安徽省淮北市濉溪城关中心校 安徽省阜阳市北城小学

数学概念的教学一般有两种方法：一是概念的同化，二是概念的形成.本节课通过《九章算术》卷九勾股中记载有趣的实例及一组数据规律问题，让学生动脑思考，在探索中发现问题，总结概括规律，建立数学模型，从而得出一元二次方程的标准形式及相关概念.再通过例子，让学生在认知中产生冲突，进一步辨析概念，巩固知识,化解矛盾.

一元二次方程;一般形式;方程的解

数学概念是学生进行数学判断和推理的基础.因此，数学概念的学习，是数学定理、法则、公式学习的基础.但是，数学概念的掌握，绝不能依赖死记硬背，而应以理解为基础，并在知识的应用中不断巩固和深化.否则，就会出现老师常见的现象：上课讲了好几遍的内容学生作业上、考试中还是错，无论怎样强调，学生就是改正不过来.其主要原因是学生没有理解数学概念，而是囫囵吞枣，消化不良，没有掌握数学概念的实质.为了解决这个问题，很多教师试图在课堂上通过“教师多讲、多加注释，学生多听、多记笔记”的策略促进学生掌握数学概念.结果表明，这种方法是收效甚微的.

课程标准明确指出，为了帮助学生真正理解数学知识，教师应注重数学知识的形成过程，组织学生开展实验、操作、尝试、观察、分析，抽象概括等活动.本文以“一元二次方程”概念的学习为例，阐释如何设计问题情境，经历概念形成过程，促进学生的有效理解.

1 “一元二次方程”教学实录与评析

教学目标：(1)了解一元二次方程及有关概念；

(2)能够运用一元二次方程的概念解决一些简单的问题；

(3)在探索问题的过程中,体会一元二次方程的模型，体会方程与实际生活的联系；

(4)通过有趣的实例，让学生合作探究，建立数学模型,从而得出一元二次方程的概念；

(5)经过问题解决，体会数学知识的运用价值，提高学生学习兴趣.

重点 一元二次方程的概念及一般形式

难点 建立一元二次方程模型

1.1 概念的引入

教师：《九章算术》卷九勾股中记载：今有户不知高广，竿不知长短.横之不出四尺，纵之不出二尺，斜之适出.问户高、广、斜各几何？

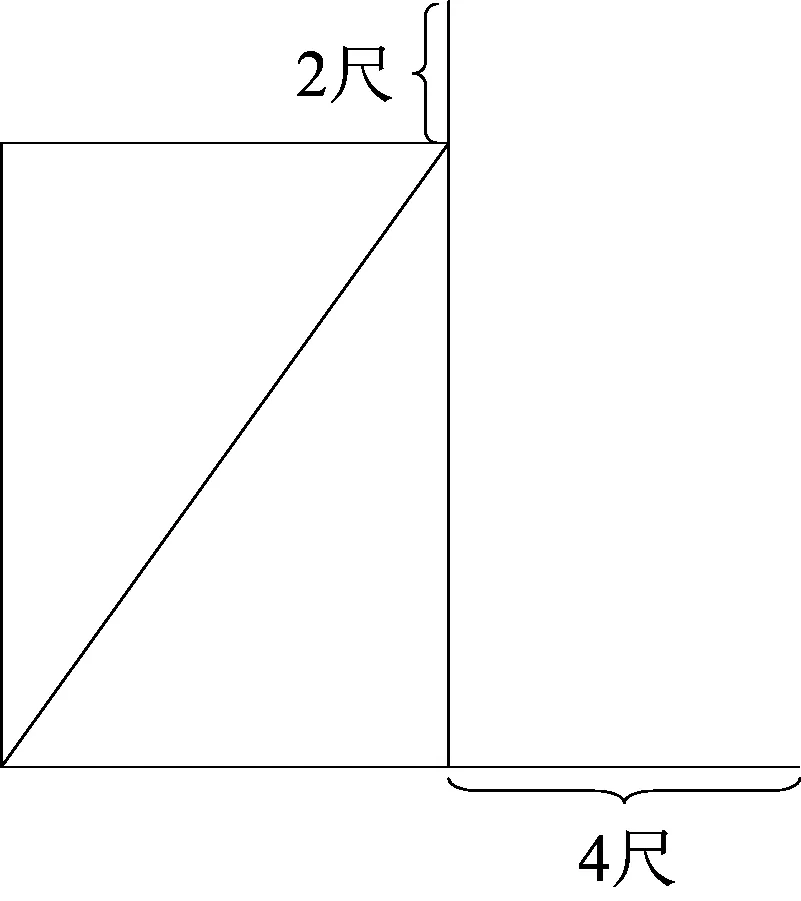
先请语文科代表翻译后,再大家画出示意图：

学生1：设矩形的斜长为x，利用勾股定理对斜长计算可以得到方程:(x-4)2+(x-2)2=x2.

学生2：设矩形的宽为t，可列出方程：

t2+(t+2)2=(t+4)2

学生3：设高为s，可列出方程：

(s-2)2+t2=(s+2)2

评析 教师利用《九章算术》中的勾股材料引入，学生觉得非常有趣，同时体现了一元二次方程在解决几何问题中的应用.

教师：请观察下面等式，还有哪些整数也满足这关系？

102+112+122=132+142

学生4：11，12，13，14，15

学生5：不成立，因为112+122+132=434，而142+152=421，所以不成立.

学生6：我发现并不是所有的整数都满足这个关系，所以很难猜出来，我可以设满足的这个数为x,它满足这样的方程：

x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2

学生都表示赞同.

评析 教师精选了这样一个等式，一般的学生都认为是满足一般情况的一个特例，谁知将11，12，13，14，15代入不成立，马上产生了认知冲突，进一步激发了学生学习的兴趣，也体现了一元二次方程在解决代数问题中的应用.

1.2 概念的形成

教师：大家观察一下，黑板上大家列出来的四个方程和我们学过的一元一次方程、二元一次方程、分式方程有什么区别和联系.

学生7：等式两边都是整式，都只有一个未知数，未知数最高次为2次的方程.

教师：很好，你能把满足这四个条件的等式取个名称吗？

学生：都喊出“一元二次方程”.

评析 教师通过让学生比较引入中得出的方程和已学方程的联系与区别，轻松得出一元二次方程概念的四个要点，加深了数学理解.

1.3 概念的辨析

(1)下列方程哪些是一元二次方程？

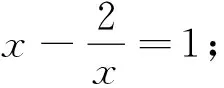
学生8：②④⑤⑥

学生9：我觉得⑥不是，因为化简后变成6x+7=0，所以它是一元一次方程.

学生8:我觉得它就是一元二次方程，因为它完全满足概念中的四个条件.

学生觉得都有道理，满脸疑惑地看着老师.

教师：我也觉得两位同学都很有道理，那数学上到底是怎么约定的呢？我们现在只有以书本为准.书上是这样约定的：ax2+bx+c=0 (a、b、c为常数，a≠0)称为一元二次方程的一般形式.

学生马上就明白了.

评析 一开始以为第⑥个问题是教师的疏漏，导致学生产生无谓的争论.结果发现这是教师的精心预设，故意给学生一个情景，引发学生不同的争论后引出书本中一元二次方程一般式的概念，加深印象.

学生10：老师，我觉得④也不对.不满足左右两边都是整式的要求.

教师：我们有办法帮这位同学解决这个疑惑吗？

学生：化简后看它是否满足一元二次方程的一般形式？

教师：好的，大家说，我来写：

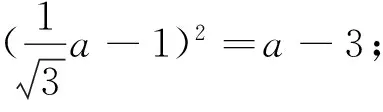
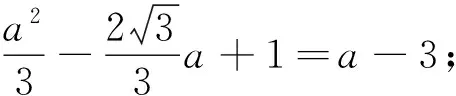
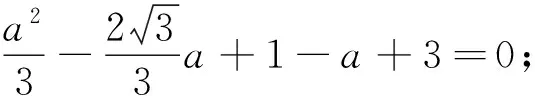
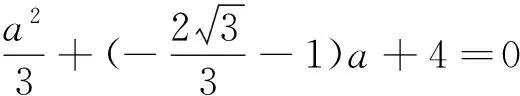
现在大家觉得④是一元二次方程吗？

有疑惑的学生脸上显露出高兴的神情，同意它是一元二次方程.

评析 个别学生对问题④的疑问是教师预设之外的，教师的耐心讲解让我佩服，这种对不同层次学生的伦理关注是课堂教学的最高关注.更让人佩服的是教师在问题讲解过程中，很好地示范了一个复杂的非标准一般式是如何转化成标准一般式的过程，为概念的简单应用做好了准备.

1.4 概念的简单应用

(1)填一填

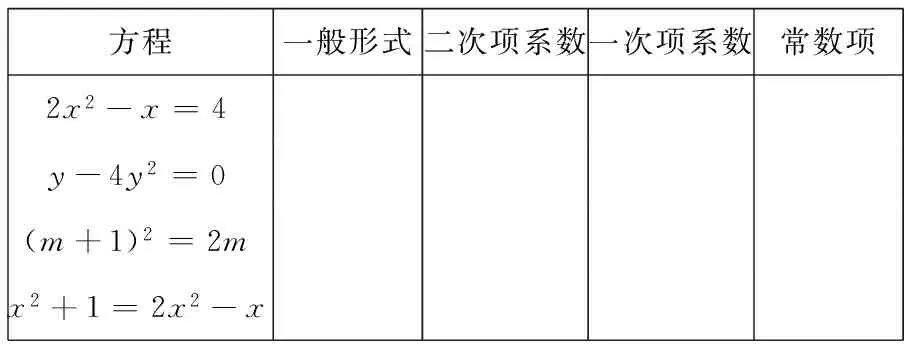
方程一般形式二次项系数一次项系数常数项2x2-x=4y-4y2=0(m+1)2=2mx2+1=2x2-x

(2)练一练1

1.关于x的方程(k2-1)x2+2(k-1)x+2k+2=0，当k______时，为一元二次方程；当k______时，为一元一次方程.

2.关于x的方程(m-1)xm+1+5x=13是一元二次方程，则m=______.

教师：做完这组题你能有怎样的“题后反思”？

学生：既要考虑系数，还要考虑次数.

评析 在一元二次方程一般式讲解后及时进行巩固练习，对系数和次数的要求进行了变式训练，起到了知识巩固的良好效果.

1.5 概念的深入理解

教师：你能猜出方程

x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2

的其中一个解吗？

学生11:x=10.

教师：怎么说明x=10是该方程的一个解呢？

学生11：把x=10代入方程，左边的值和右边的值都是365，所以x=10是方程的解.

教师：你们能类比一元一次方程解的定义，给一元二次方程的解下个定义吗？

学生12：能使一元二次方程两边相等的未知数的值叫一元二次方程的解(或根).

评析 教师利用概念引入中的例子，学生非常快地找出其中一个解，通过类比，激活已有知识，顺利地得出一元二次方程的解的定义.

练一练2：

判断下列各题括号内未知数的值是不是方程的根.

(1)2x2-5x+3=0(x1=0,x2=1)

(2)3x2-4x+7=0(x1=-1,x2=1)

学生13：x1=0不是方程(1)的解，x2=1是方程(1)的解；x1=-1不是方程(2)的解，x2=1是方程(2)的解.

教师：你有什么发现吗？

学生14：解为x=1的一元二次方程不止一个.

教师：你还能写一个方程，使它的解也是x=1吗？写完后，组内讨论所有解为x=1的一元二次方程的特点？

学生15：有一个解为x=1的一元二次方程的一般式ax2+bx+c=0 (a,b,c为常数，a≠0)中的系数有如下关系：a+b+c=0.

教师：很好，你们还能得出哪些结论？

学生16：形如ax2+(b-a)x-b=0(a≠0)的一元二次方程一定有一个解为x=1.

学生17：这个方程的左边代数式有一个因式为x-1.

教师：很厉害啊，大家还有吗？

学生18：反过来，若知道a+b+c=0，则ax2+bx+c=0 (a,b,c为常数，a≠0)有一个解为x=1.还有，若有一个解为x=0，则c=0；若有一个解为x=2，则4a+2b+c=0；若有一个解为x=3，则9a+3b+c=0…

其他学生一下子恍然大悟.

评析 教师对“练一练2”的设计非常巧妙，一开始以为就是为了练习巩固解的定义而设计的一组题目.当教师问道“你有什么发现吗？”“你还能写一个方程的解也是x=1吗？写完后，组内讨论所有解为x=1的一元二次方程有什么特点？”时，我发现教师的预设真是高明，学生的回答也证明了教师提问设计的有效性.

1.6 概念的实际应用

练一练3：

1.已知x=1是一元二次方程

(k-1)x2-kx+k2=0的一个根，求k的值

2.已知一元二次方程2x2+bx+c=0的两个根为x1=1和x2=2，求b,c的值

教师：做完后，你有怎样的题后反思？

学生19：利用解的定义，通过待定系数法，可以求一元二次方程的字母系数；还要注意一元二次方程的二次项系数不等于0.

评析 教师设计“练一练3”不但体现了学生对解的定义的灵活应用，也突出强化了本节课的一个易错点：一元二次方程一般式的二次项系数不等于0.

1.7 课堂小结，形成思维导图

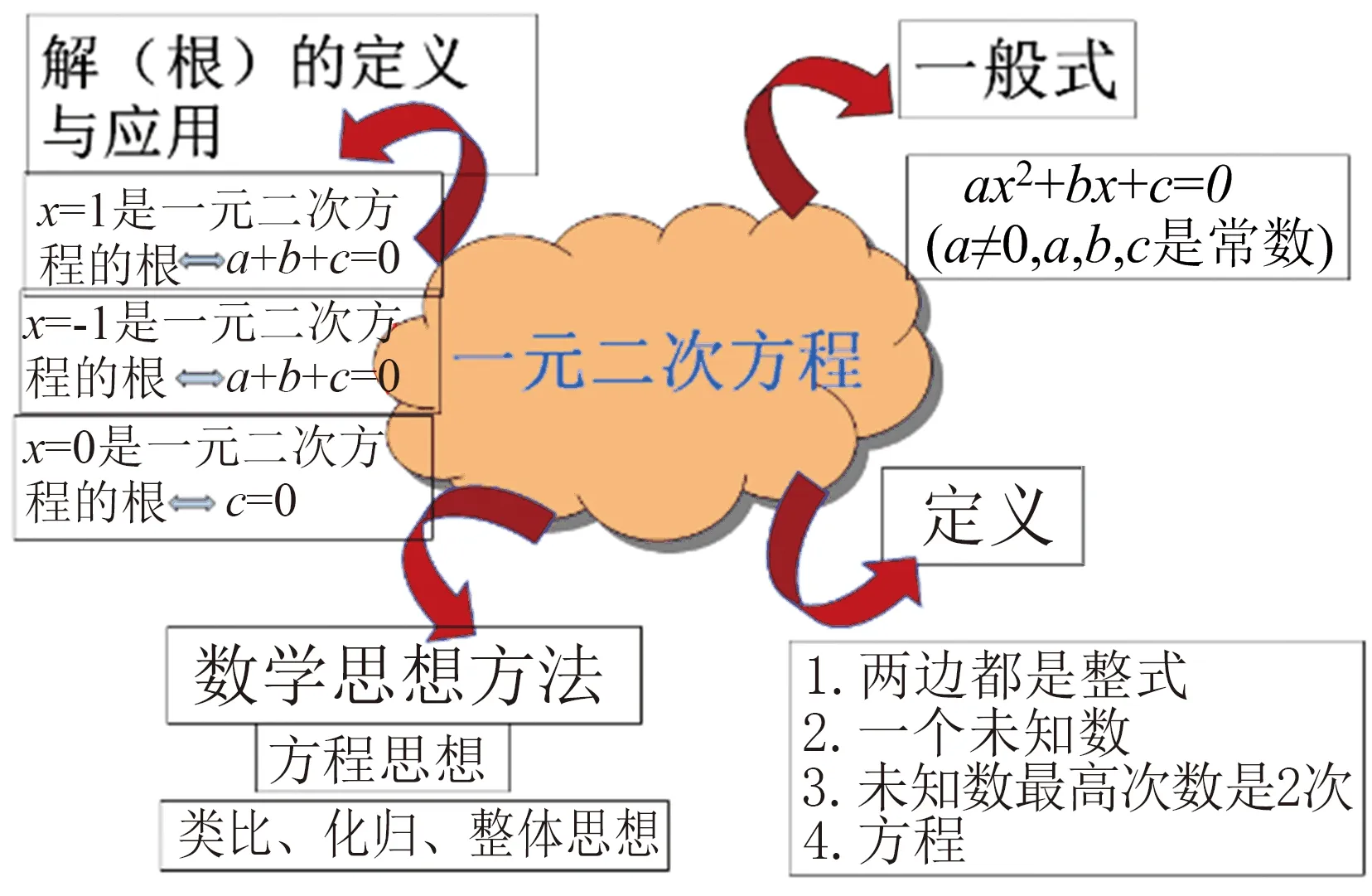
教师：我们已经学习了一元一次方程和一元二次方程，它们属于整式方程.还学习了分式方程，分式方程和整式方程统称有理方程，以后我们还要学习无理方程，比如根式方程.

评析 课堂小结中思维导图的应用，将学生所学知识很好地进行了梳理，教师最后的总结，更是将今天所学的一元二次方程概念纳入了整个数学体系中，促进了概念的牢固掌握.

2 启示

“一元二次方程”概念的学习是在杜宾斯基的APOS理论指导下设计的.本文通过设计系列问题情境，让学生经历操作(Action)，过程(Process)，对象(Object)，图式(Scheme)四个阶段，体验数学概念的形成过程，进而理解和把握数学概念的实质.

2.1 创设问题情景，引导学生操作，体现学习必要性

在教师的引导下，学生只有经历操作活动，才能为概念的形成打下基础.当然，只有当学生充分认识到概念学习的必要性，才会变要我学为我要学，发挥主观能动性.本节课“概念引入环节”中两个例子的设计就充分体现了一元二次方程在解决代数和几何两大数学问题中都有重要应用，体现了学习一元二次方程的必要性，激发了学生学习的兴趣.

2.2 创设问题情景，引发认知冲突，促进学生内化.

课堂教学中，不仅仅是在课堂引入中需要创设问题情景.更需要在教学过程中创设问题情景，引发学生的认知冲突，在一个个问题的解决过程中学生收获的是对数学的理解，对数学真正的热爱.比如本堂课教学设计的概念辨析环节中，教师精心设计第⑥个算式，引发学生对一元二次方程概念的认知冲突，从而引出数学书中对一元二次方程一般式的约定.

教师有效的创设问题情景，也能引发学生有效的数学思考.比如教师在“概念深入理解”环节中，通过创设两个一元二次方程都有解x=1这样一个情景，设计了一系列有梯度的问题“你有什么发现吗？”“你还能写一个方程的解也是x=1吗？”“组内讨论所有解为x=1的一元二次方程有什么特点？”“你还能得出哪些结论？”引发学生深入的数学思考.

2.3 创设问题情景，积累活动经验，提高应用能力.

学习数学的过程就是经验积累的过程，教学过程中设计变式训练，可以加深对易错点的理解，积累学生的解题活动经验.比如在“概念的简单应用中”，教师设计的“填一填”，“练一练1”,都设置了变式训练，为学生熟悉一元二次方程的非标准形式和深入理解一元二次方程一般式中对未知数次数和系数的要求起到很好的效果.

2.4 利用思维导图，促进形成图式，渗透数学思想.

图式是操作、过程、对象和以前的子图式的综合体.只有学生在头脑中拥有了有效的图式，相应的数学结构才能形成.本节课，通过思维导图的绘制，帮助学生以“一元二次方程”为核心，建构子图式.当然，更大的图式不是一次完成的，需要不断地螺旋上升，从而形成数学思想.

1 曹才翰.中学数学教学概论[M].北京：北京师范大学出版社，1990

2 中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[S].北京：北京师范大学出版社，2012

3 孔凡哲.数学学习心理学[M].北京：北京大学出版社，2012

2016-12-26)