纵横串联 构建体系——以《三角形边的中点》专题复习为例

王敏敏 (邮编：230022)

安徽省合肥市包河区海顿学校

纵横串联 构建体系
——以《三角形边的中点》专题复习为例

王敏敏 (邮编：230022)

安徽省合肥市包河区海顿学校

复习课是一种基本课型，它承载着“回顾与整理、沟通与生长”的独特功能.探究式课堂教学就是在教师的启发诱导下，以学生独立思考、探索交流为前提，为学生提供充分自由表达、质疑、探究、讨论问题的机会，让学生通过个人、小组、集体等多种解难释疑的尝试活动，将自己所学的知识应用于解决问题的一种教学方式.把探究式教学应用于复习课中，必然会使复习课因此而绚丽多彩！

复习课;探究式;学习兴趣;系统化;高效课堂

作为数学教学常规性工作的复习课，它的重要性不言而喻，双基要在复习中巩固，数学思想方法要在复习中加深理解，活动经验要在复习中逐步积累，相关知识的联系在复习中更加紧密，解决问题的能力也正是在复习中得到培养和加强.学生通过复习，对数学的基础知识准确熟练地掌握，使这些知识在头脑中竖成串，横成链，形成知识网络，进而形成知识体系；同时也能弥补自己在新课教学中的不足.笔者做了一些尝试，希望能带给学生一种全新的复习课.

1 复习课的现状

上一节课容易，上好一节课很难！上好一节复习课更是难上加难！一线教师难免会发出这样的感叹.如火如荼的课堂教学改革更多关注的是新授课教学，复习课成了被改革遗忘的角落.目前的复习课要么是单纯地疏通知识点.复习是一个疏通知识的过程，它必须理清知识之间的联系，将“点”连成“片”内化为学生的东西.然而我们在教学中往往过分强调了疏通知识点，只强调知识技巧的掌握，而忽视了能力的培养.要么上成了练习课.“复习”课需要练习但不应是为练习而练习.我们在教学中总是练习层层递进，密度不断加大，角度依次变换，难度随之增加.一堂课下来教师很辛苦，学生很痛苦，事倍功半.时间久了，学生对数学也就失去了兴趣.不管上出什么样，最重要的一点是给学生空间不多.上“复习”课时，老师往往表现得主观意识很强，过度发挥了主导作用，很少照顾到学生会怎么想，会怎么说，会怎么做.不是沿着学生的思路去分析问题、解决问题，而是把学生引入自己的思路中，阻碍了学生的思维发展.在教学中缺少教师与学生的交流、学生与学生的交流、学生与教材的交流，使学生始终处于被动的地位.老师们忽视发散思维，知识迁移不够.教师往往重知识系统本身，很少引导学生思考与系统有关的知识，即很少举一反三，让学生思维发散，实现知识迁移.

概念或知识回顾、例题讲解、巩固练习，没有针对性、忽视学生自主探究、忽视数学思想方法乃至文化的渗透和熏陶.存在问题的原因是：应试教育根深蒂固，教师观念没有彻底转变，评价工具落后(作为评价的试题，可以通过反复、机械训练来提高成绩)等等.

2 我是如何看复习课的

究其原因，复习课包含了两方面的内容，一方面要对学过的知识进行归纳整理，使零散的知识系统化、整体化、结构化；另一方面要加强知识的迁移训练，使学生对知识的运用熟能生巧、举一反三，从而达到灵活运用的层次.对于前者，如果在课堂上只是进行机械地罗列知识点，无疑会使复习课变得索然无味；对于后者，由于知识的发散点很多，一些老师就感到束手无策，抛弃了知识技能的整理，选择以题海代复习.这两种情况必然会导致一个结果：学生的能力止步不前或进步不大，最终导致复习并没有达到预期的效果.众所周知，复习课包括经常性复习和阶段性复习两个方面.不同的复习课有一定的差异性，但是，它们有着共同的规律.作为一节复习课，首先要回归基础，完善知识体系.在我们整个初中阶段，定义的介绍、定理的证明、公式的推导以及其中蕴含的数学思想方法分散在不同阶段、不同内容的教学中，复习课就要按照其内在的逻辑关系将它们进行整理，学生的知识才会系统化、结构化，才能通过顺应和同化的过程，形成良好的认知结构.其次，复习课还要加强联系和综合，提高数学能力.在充分做好双基复习和训练的基础上，例题的选取也起到了关键性的作用，要针对核心概念、基础知识，不能追求“特技”，要强调通性通法，具有基础性；不能人为拼凑，简单堆积，要做到基础知识与基本思想方法的自然沟通，兼顾综合性.波利亚提出：一个重大的发现可以解决一道重大的题目，但是在解答任何一道题目的过程中都会有点滴的发现.从这个角度而言，典型例题的选择要立足于启迪学生从新的角度看待问题，通过沟通知识和方法形成新的解题方法，激发思维的创造力.

3 案例呈现

3.1 学什么——内容确定

三角形是课程标准中要求学生必须要掌握的内容之一，其中，三角形边的中点更是有着举足轻重的地位，许多问题的解决，或多或少的都会选择以此为突破口，同学们如果能把这个小知识点的相关知识相互串联起来，做到融会贯通，那么对于他们分析问题、解决问题能力的提高，无疑会是一个很大的帮助.专题复习要求所选的知识点以及所涉及的思想方法，可以帮助我们解决很多问题，而复习专题的选择，也正是为了学生知识与能力的提高.基于这些，笔者认为有必要把本节课单独拿出来作为九年级第二轮复习的一个专题复习.

3.2 怎么学——案例呈现

(1)预学——梳理知识，准备学习

问题1 回忆三角形边的中点的相关知识，加以整理并选择合适的方式表示出来；把结果和伙伴分享并完善.

设计意图 通过回忆按照内在的逻辑联系将所学知识进行整理，参与归纳整理的过程，学生自己梳理知识，体现自主性原则；用适当的方式表示出来，把零散的知识串成串，使学生头脑中的知识系统化、结构化，形成良好的的数学认知结构，顺应了系统化原则，这两个环节是对知识“忆”的过程；把结果和同伴分享并完善，就是针对自己的薄弱环节和存在的问题，进一步深化学习，采用同伴互助的方式可以逐步培养学生合作学习的意识，符合针对性原则，使复习有的放矢，这是对知识“清”的过程；

(2)自学——联想迁移，自主学习

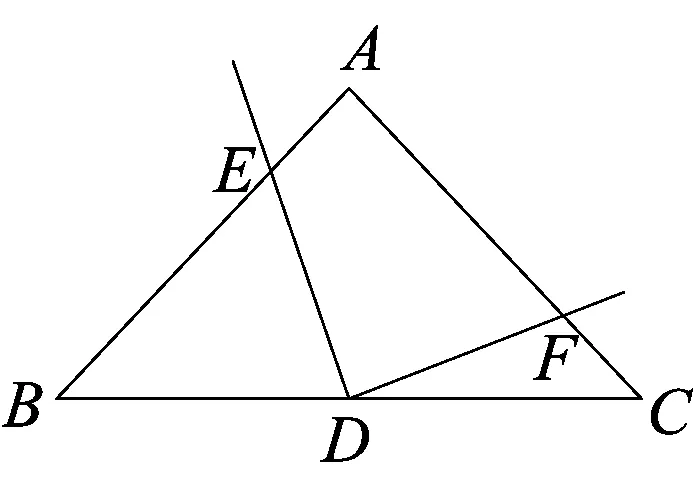
图1

图2

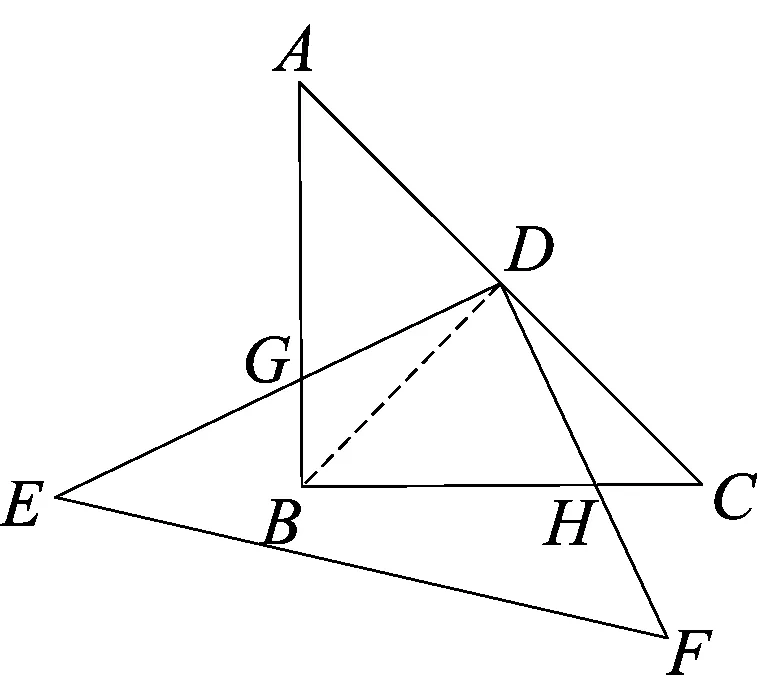
图3

图4

问题2 在△ABC中，点D为BC边的中点，以点D为顶点的∠EDF的两边分别与边AB、AC交于点E、F，且∠EDF与∠A互补.如图1，若AB=AC，且∠A=90°，则线段DE与DF有何数量关系？请给出证明.

师生活动 老师给出问题后，立刻就有学生给出自己的想法：DE=DF.他联想到曾经做过的一道书本练习：如图2，△DEF的直角顶点与等腰直角△ABC的斜边上的中点D重合，两条直角边DE、DF分别与AB、AC边交于G、H两点.试说明DG与DH的关系.通过同学们的展示，发现他们大多采用以下方法解决：

解法一 如图3，连接DB，证明△DGB与△DHC(或者△ADG与△BDH)全等，说明DG与DH相等.

解法二 如图4，过点D作DM⊥AB,DN⊥BC,证明△DMG与△DNH全等，说明DG与DH相等.

(3)助学——师导生助，探究学习

问题3 想得到DE=DF这一结论，你认为AB=AC和∠A=90°中的哪个条件在这个问题中是必需的？请给出证明.

师生活动 教师给出问题后，要求同学们先独立思考，遇到障碍时可以与同伴交流讨论，合作探究.

同学们在交流讨论的时候，把这个问题转化成为下面两个问题来解决：

图5

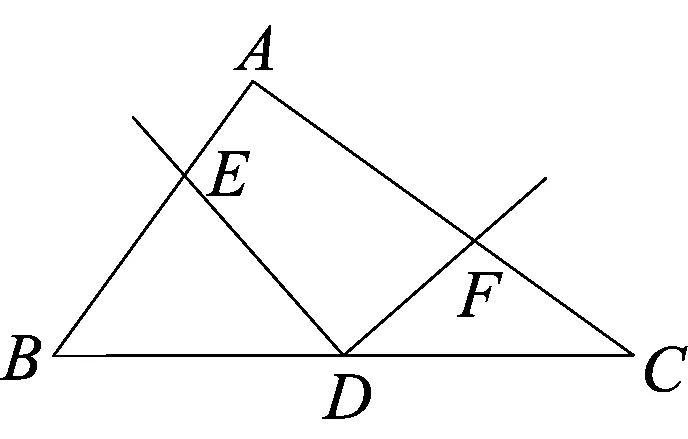
图6

图7

图8

①如图5，若仅AB=AC，那么DE=DF是否仍然成立？若成立，请给出证明；若不成立，请说明理由.

②如图6，若仅∠A=90°，那么DE=DF是否仍然成立？若成立，请给出证明；若不成立，请说明理由.

对于①，采用解法一的同学发现一旦没有了直角三角形，就变得寸步难行；但是采用解法二的同学却发现，去掉了∠A=90°这一特殊条件，那么由此产生的特殊化图形中位线以及正方形MDNB也就不复存在了.但是，如图7，当过点D分别作DG⊥AB，DH⊥AC后，仍然可以借助等腰三角形的三线合一说明DG=DH，从而证明△DMG与△DNH全等，同样可以得出DE=DF的结论.

对于②，采用解法一的同学虽然会找到直角，得出直角三角形斜边上的中线等于斜边的一半，但是，全等的三角形却不见了.采用解法二的同学却发现，当过点D分别作DG⊥AB，DH⊥AC后，却出现了一个矩形AGDH,再借助于∠EDF=90°， 就可以说明△DEG∽△DFH,由于DG和DH不等，所以DE和DF也就不相等了.

问题4 在△ABC中，点D为BC边的中点，以点D为顶点的∠EDF的两边分别与边AB、AC交于点E、F，且∠EDF与∠A互补.如图9，一般的，若AB∶AC=m∶n,请你探索线段DE与DF的数量关系，并证明你的结论.

图9

设计意图 典型例题的探究以三角形一边上的中线在解决问题时所起到的作用为例进行，希望能够起到抛砖引玉的作用，引发同学们在课下对有关三角形中位线的问题加以探究，两者互相结合，完成知识的迁移训练，这是对知识“析”和“练”的过程.

(4)悟学——体会感悟，完善学习

问题5 你学到了什么？

你感受到了什么？

你还想知道什么？

你不明白的是什么？

设计意图 对于前两个“什么”，是对本节课涉及的问题进行探究与思考，并总结这一类问题该如何尝试解决.第三个“什么”的提出，意在引出和三角形边的中点还有哪些典型的问题，请同学们课后思考.在学生已有的认知基础上，让学生是对本节课的学习从知识、方法、情感等方面谈谈自己的体验和感悟.问题中的四个“什么”，目的是培养学生总结提升的能力，激发学生的探究新知的欲望.

3.3 学得怎么样——能力检验

学得怎么样可以通过很多途径来评价，对类似问题的解决情况无疑是最好的衡量方式.本节课的复习内容恰好迎合了2016年安徽中考数学卷的压轴题.

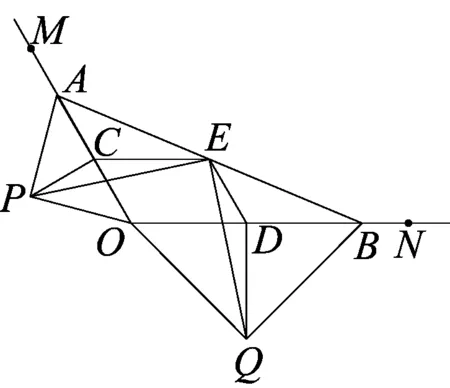
图10

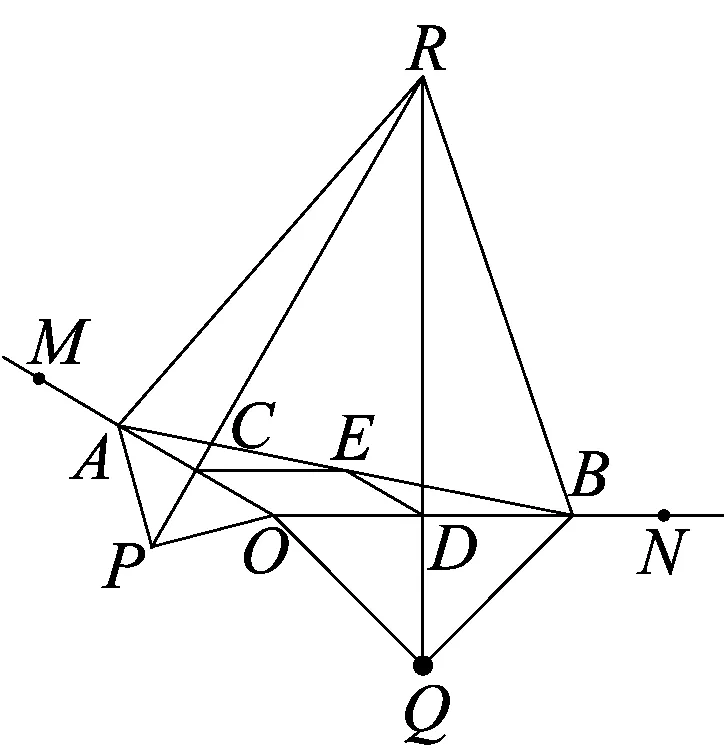
图11

图12

如图10，A、B分别在射线OM、ON上，且∠MON为钝角，现以OA、OB为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP、△OBQ，点C、D、E分别是OA、OB、AB的中点.

⑴求证：△PCE≌△EDQ.

⑵延长PC、QD交于点R.

①如图11，若∠MON=150°，求证：△ABR为等边三角形.

图13

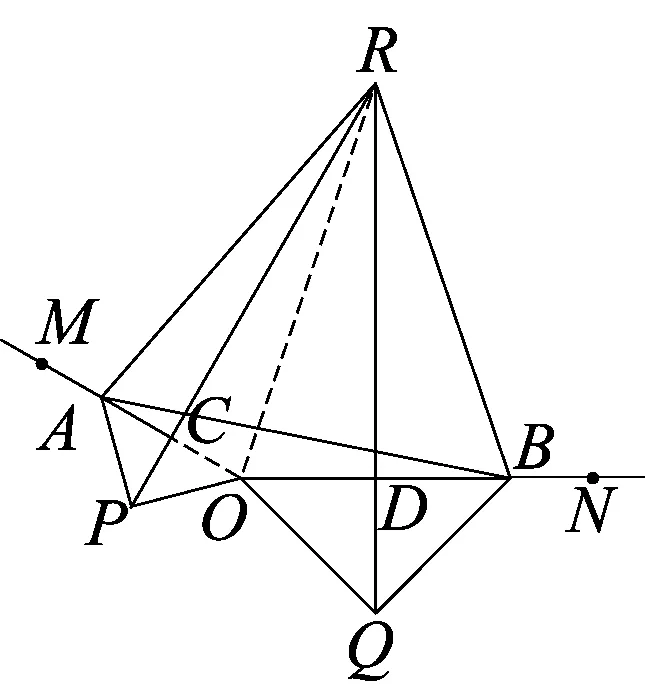
图14

②如图12，若△ARB∽△PEQ，求∠MON的大小和AB比PQ的值.

作为一张试卷的压轴题，它承载着很多很多.对于本题，我们不难看出它的第一问和第二问的前一小问，分别考查了三角形的中位线和等腰三角形底边上的中线两个知识点的迁移应用.

考试结束后，我询问了部分同学.同学们大多认为，本题带来的最大的困扰，就是图形过于复杂.也有不少同学关注到了本节课的复习内容，通过阅读题干，很容易找到了关键性的条件——两个等腰直角三角形和三个中点.点C、D、E分别是OA、OB、AB的中点，就很容易得出了四边形CODE是平行四边形；不仅如此，他们还发现，点C、D分别是OA、OB的中点，还可以得出，PC和QD分别为两个等腰直角三角形斜边上的中线，观察至此第一小问就迎刃而解.

关于第二小问，看上去似乎和中点问题关系不大，题目要求延长PC、QD交于点R，有些同学就观察PC、QD在图形中处于什么位置，结合图形阅读题干，发现PC和QD分别是两个等腰直角三角形斜边上的中线，想到这恰恰正是我们在专题复习课中重点强调的知识，自然得出了RP和RQ分别是线段OA、OB的垂直平分线，于是，就选择连接OR(如图13所示)，△ABR为等边三角形就呼之欲出了.更为可喜的是，有些同学们在解决问题的时候，能够将与本题无关的图形剔除(如图14所示)，使问题的解决变得更加容易.对于后半部分，相对于前两个问题而言增加了一些难度，能够解决的同学不多.如图12，有个别同学解释自己的思路说到，想求出∠MON的大小，RP和RQ分别是线段OA、OB的垂直平分线，仍将发挥巨大的作用，有了这两条线段的中垂线，就会出现∠MON+∠CRD=180°，要想求出∠MON的大小，只需要求出∠CRD的度数即可；这时，仍然需要，RP和RQ分别是线段OA、OB的垂直平分线来告诉我们：∠CRD的度数是∠ARB度数的一半.只要想办法求出∠ARB的度数就可以解决问题了.结合题目已知条件：△ARB∽△PEQ，可以通过求∠PEQ的度数来达成目的，进一步观察图形可以看出：∠PEQ=∠DEC-∠CEP-∠DEQ，通过DE∥OA，可以得出∠DEC=∠ACE，再由第一问的结论：△PCE≌△EDQ，可以得出∠CPE=∠DEQ，于是可得：∠PEQ=∠DEC-∠CEP-∠DEQ=∠ACE-∠CEP-∠CPE=∠ACR=90°，从而得出△PEQ是等腰直角三角形.

听完同学们的介绍，我心头暗喜.纵观本题的解决过程，中点的影子随处可见！我们常常以为，压轴题就应该考查函数、相似等一些看似高大上的知识点，而一个小小的中点在这里却也可以成为弄潮儿，我们不免感叹！

这也恰恰提醒我们注意，复习课要从大处着眼，小处入手，课堂上只要能选择一些激励性的问题去帮助学生解答题目，就能培养学生对独立思考的兴趣，并教给他们某些方法.我们如果可以把初中数学中一个个看似其貌不扬的小知识点弄透彻，何愁大的知识体系不能完善？

4 写在最后

复习课难上，一方面它是“新课题，旧知识”，知识都是学生学过的，复习课的任务要引导学生对这些知识进行整理，找到它们之间的联系，通过对它们的重新概括形成良好的数学认知结构，再结合一定的训练，提高解决问题的能力.另一方面复习课内容多，时间少.这必然要求作为教师的我们，一方面要把具有很强迁移能力的核心概念、思想方法作为复习的重点，另一方面更要选择合适的教学方法尽力引导学生，把注意力集中在数学的核心概念和基本思想方法上来.而探究学习重视科学的结果更重视获得的过程，重视知识的获得更重视知识的运用.采用探究的方式展开教学，更加有利于培养学生牢固的基础知识、高层次的思维能力以及自主学习的能力.形象地说，平时教学像"栽活一棵树"，考前复习似"育好一片林".栽活一棵树容易，育好一片林要花功夫.要我们用心去做，相信每一个人都可以让自己的那片林风光更美！

1 孔凡哲，崔英梅.课堂教学新方式及其课堂处理技巧：基本方法与典型案例[M].福州：福建教育出版社，2011:81-88

2 章建跃，曹才翰.中学数学教学概论[M].北京：师范大学出版社,2008:488-495

3 罗增儒.怎样解答中考数学题[M].西安：陕西师大出版社,1996

2017-01-10)