对称不等式的解题技巧探究

☉上海复旦附中高三（4）班 梅灵捷（指导老师：汪杰良）

对称不等式的解题技巧探究

☉上海复旦附中高三（4）班 梅灵捷（指导老师：汪杰良）

在不等式中，变量拥有着两两之间的对称性或轮换性，统称为对称性不等式.破坏对称性是指通过规定顺序、指定最值等方式，打破不等式原先固有的对称性，从而达到简化不等式或方便估计的思想方法.该思想在对称的代数不等式和组合不等式上较为有用.

证明：不妨令c=min｛a，b，c｝，

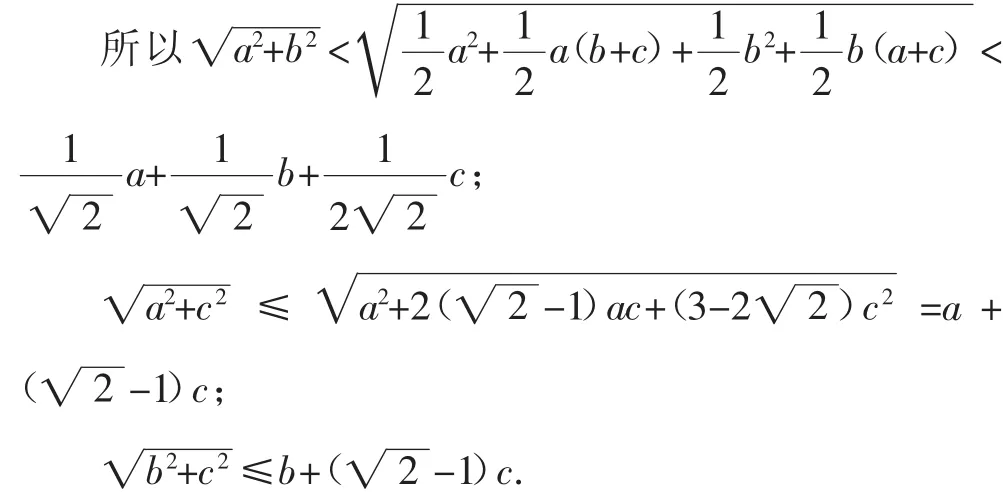
说明：无限趋近于等号的条件是两边相等，一边趋向于零.也就是说，有两条最长边.这也为我们的估计增加了两种可以套用的不等式.当遇到不对称的取等条件时，我们可以使用破坏对称性的思想.通过变元之间的部分替换，可以将表达式内界决定上界的那一部分进行转化，以达到使估计精确的目的.

例2 集合S⊂Z+，|S|=n，对于集合A，B，其中A，B⊆S且的最小值［2］

解析：令S的元素为a1≤a2≤…≤an.

Tm=｛ai|1≤i≤m，i∈N｝有2|Tm|-1=2m-1个非空子集，且每两个非空子集的元素和不同⇒元素和最大的子集Tm元素和为

以下对m使用数学归纳法.

（2）假设m=k成立，令m=k+1.

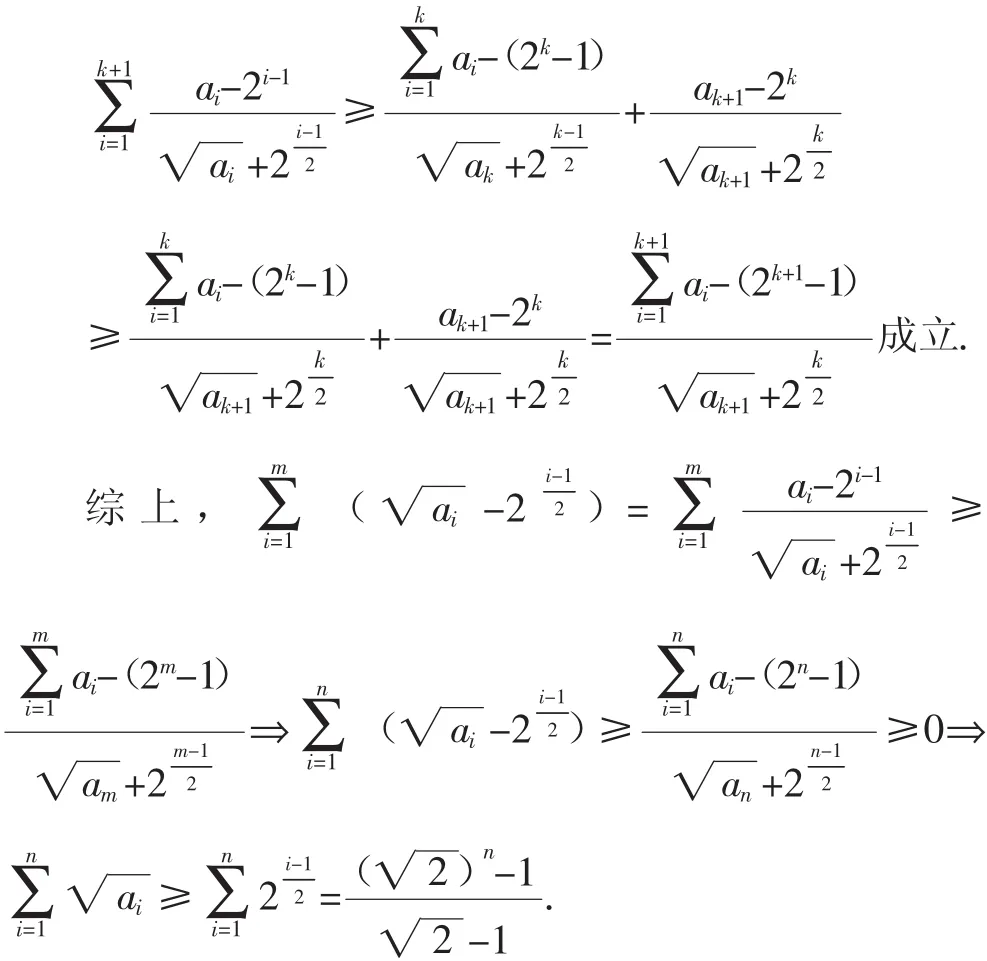
当且仅当ai=2i-1时取等号.

说明：我们并不能控制S指定一个元素的范围，因为元素的排列远不如它们的和稠密.因而需要通过对一定个数元素的和进行估计.关键在于一定个数元素的和中最小的那一个如何确定.

注意到在解答中多次出现了将ai与2i-1进行比较的情况，这是由ai之间的顺序保证的.将两个在取等条件下相等的数作差，可以将差放大，估计精细.

例3 （2013年土耳其数学奥林匹克第二轮）求m的最大值，使得∀a，b，c∈R+，a3+b3+c3-3abc≥m（ab2+bc2+ ca2-3abc）.

分析：首先可以看出，a，b，c的地位是不同的，这也与原式右边是轮换非对称式相符.因而我们可以破坏对称性，使得限制m的范围时等式两边都不为零.注意原式右侧是轮换非对称式，只能取定最大或最小或中间值，不能固定顺序.

解：当a=b=c时一定成立.当a，b，c不全相等时，a3+b3+ c3-3abc，ab2+bc2+ca2-3abc＞0.

原题转化为求满足∀a，b，c∈R+，m≤时m的最大值.

不妨令a=min｛a，b，c｝，以下进行分类讨论：

（1）当b≤c（a≤b≤c）时，令b-a=x，c-b=y（x，y≥0）⇒其中A，B，C，D是与a无关的正常数因而T的极小值在a→0或a→+∞时取到.

（2）当b≥c（a≤c≤b）时，（ab2+bc2+ca2-3abc）-（ac2+ cb2+ba2-3acb）=（a-b）（b-c）（c-a）≤0，即m（ab2+bc2+ca2-3abc）≤m（ac2+cb2+ba2-3acb）.

说明：在一开始，本题通过孤立变量m，将恒成立问题变为求最值问题，同时减少了一个变量，简化了运算.实际上，将T趋向为零或无穷大时，运用了调整的思想.

本题通过将破坏对称性后两种截然相反的对偶式进行比较，从而达到了化归的效果，既契合了原式右侧的轮换对称性，又缩小了篇幅.

破坏对称性思想在对称不等式证明中具有着重要的作用.破坏对称性思想可以在如下情况时使用：①有不对称的取等条件的；②内界需要进行变元替换的；③需要加强较弱估计的；④需要提炼最有价值的关系式的；⑤需要利用某些调整法的；⑥利用对偶式的差别进行化归的.通过掌握破坏对称性思想，可以解决大量使用普通方法无法完成的对称不等式.

1.苏勇，熊斌.不等式的解题方法与技巧［M］.上海：华东师范大学出版社，2005.

2.Yong-Gao Chen.Distinct subset sums and an inequality for convex functions［J］.Proc.Amer.Math.Soc. 128（2000）.

3.“Turkey National Olympiad Second Round 2013· Art of Problem Solving”，［Online［·Available：http：//www. artofproblemsolving.com/Forum/resources.php.c=174&cid= 95&year=2013.