忽如一夜春风来 素养之花遍地开——从高中数学核心素养的视角看2016年浙江高考数学试题

☉浙 江 师 范 大 学 朱伟义☉浙江师范大学特级教师工作流动站 曹凤山

忽如一夜春风来 素养之花遍地开
——从高中数学核心素养的视角看2016年浙江高考数学试题

☉浙 江 师 范 大 学 朱伟义☉浙江师范大学特级教师工作流动站 曹凤山

数学核心素养已成为热词.词是新的，而基于数学核心素养的实践与考试评价不是一夜之间突然冒出来的，核心素养的提出，是对昨天教育教学实践的提炼，更是对明天的期待.鉴于目前我国教育教学的现实，以考试评价的杠杆撬动教学改革往往很有效.高考试题命题范式已经经历了政治立意、知识立意、能力立意三个阶段，以后的命题势必转化为素养立意.从核心素养考查的角度理解高考试题，对以后的教育教学就有重要的现实意义.下面试从数学核心素养的视角解读2016浙江高考数学试题.

一、核心素养的考查是注重基础、数学本质的考查

知识与技能是素养的载体，数学素养首先表现为考生对基础知识与技能的掌握情况.

以理科试卷为例，从知识点分布看，《说明》要求的各知识模块都有考查，知识覆盖面较大.对支撑中学数学知识体系的重点知识重点考查，分数占有较大的比重，如理科的立体几何、解析几何、三角函数、函数、不等式以及数列等，在知识的交汇点上下工夫，如理科的不等式部分，结合解不等式、线性规划、大小比较、绝对值、向量运算及几何意义、函数与方程、数列等有关知识加以考查.文科的试卷也有类似的特点.

2016年浙江省高考数学（理科）各模块分值分布与考查内容分析

知识模块 分值比重考查内容集合与常用逻辑用语 10 7 集合的交、并、补运算；含有一个量词的命题的否定函数 21 14对数运算；二次函数、绝对值函数的单调性、最值以及分类讨论、数形结合、化归与转化思想等

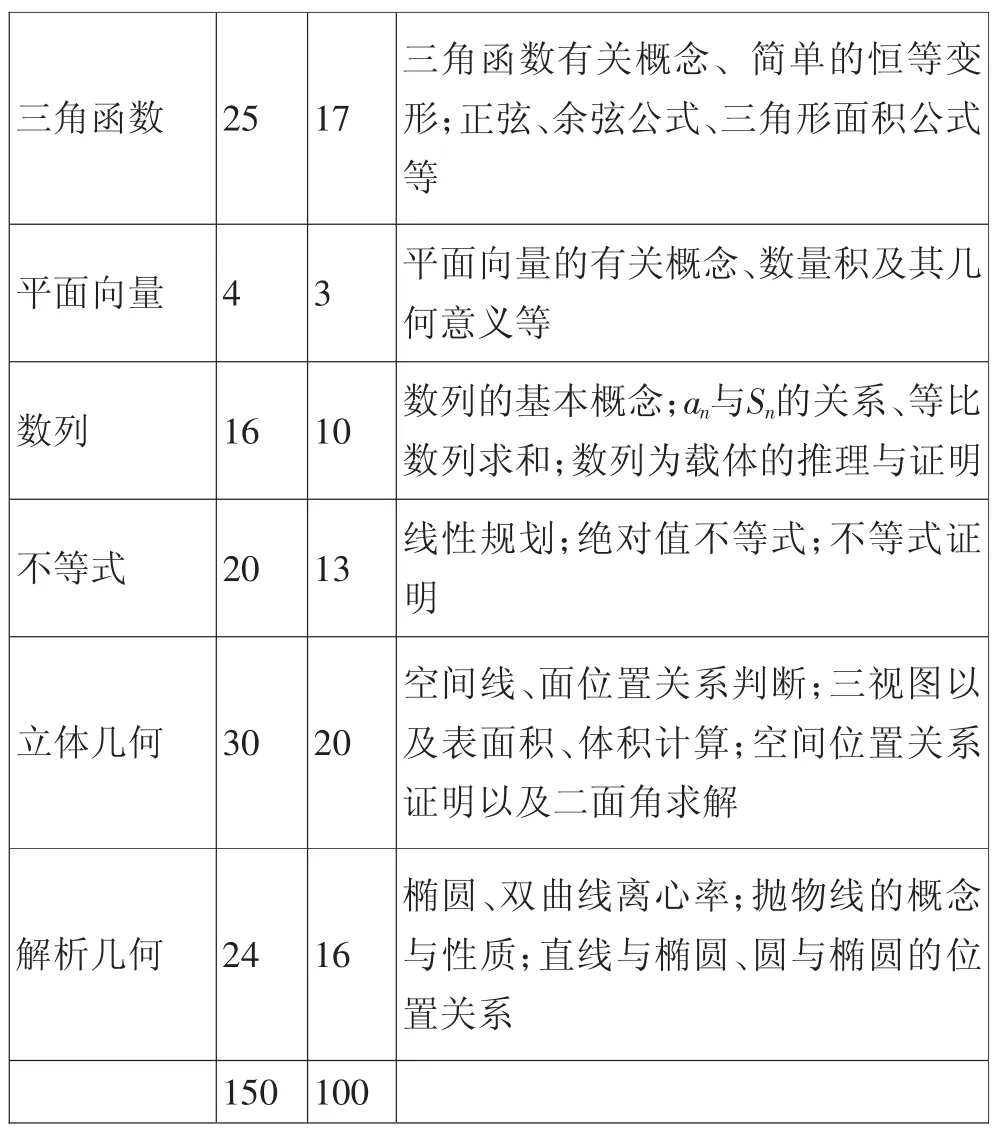
三角函数 25 17三角函数有关概念、简单的恒等变形；正弦、余弦公式、三角形面积公式等平面向量 4 3 平面向量的有关概念、数量积及其几何意义等数列 16 10 数列的基本概念；an与Sn的关系、等比数列求和；数列为载体的推理与证明不等式 20 13 线性规划；绝对值不等式；不等式证明立体几何 30 20空间线、面位置关系判断；三视图以及表面积、体积计算；空间位置关系证明以及二面角求解解析几何 24 16椭圆、双曲线离心率；抛物线的概念与性质；直线与椭圆、圆与椭圆的位置关系150 100

高考命题一方面重点关注“主干知识”，同时，也兼顾各知识板块的考查权重.高考命题在进行考查内容抽样时，关注的是如何使得所抽取的样本能够最大程度地检测考生作为未来公民所必要的数学素养的达成程度，而不是完全拘泥于知识的选取或知识与知识的机械组合，关注点是高中数学知识所涵盖的数学素养的完整性.

无知则无能.基础是素养的保证，是以后发展的基石，是高考的考查重点所在.没有基础就谈不上素养，高考以素养立意并不意味着高考试题绝对难度的整体提升.

案例1（文科第15题）已知平面向量a，b，|a|=1，|b|= 2，a·b=1.若e为平面单位向量，则|a·e|+|b·e|的最大值是______.

解析：一些考生把它当成一道计算题，甚至看到有老师也是用很长的篇幅算出结果.

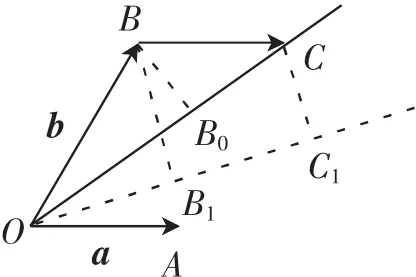
图1

实际上，由|a|=1，|b|=2，a· b=1易得＜a，b＞=60°，|a·e|+|b·e|表示向量a，b在单位向量上的投影的和，如图1，OB1+B1C1= OC1，当单位向量与a+b共线时，投影为OC，明显地，|OC1|≤|OC|，即当且仅当单位向量与a，b共线时|a·e|+|b·e|最大，这时∠OBC=120°，则|a·e|+|b·e|的最大值是理科第15题难度相比文科较大，但考查手法如出一辙，显示出命题人对考查数学本质的执着追求.

数学是简单的，数学是自然的，数学是讲道理的，因为数学是建立在概念、定理基础上的.数字严密的刻画，具体生动的形象，具体情境下的应用显示了数学概念、原理理解下的数学的价值，是数学素养的基础.

二、核心素养是注重数学思想方法的考查

凸显数学思想方法的考查，寓思想方法的考查于基础知识的考查之中，重要的思想方法在不同题型中以不同的方式考查.重点考查的数学思想方法，如数形结合思想、转化与化归思想、函数与方程思想、分类讨论思想等.

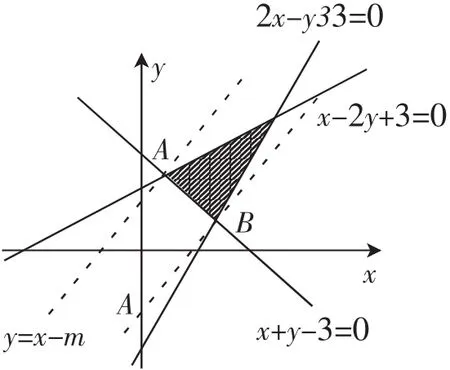
图2

解析：试题难度不大，细细思考倒也别有风味.首先画出可行域，如图2，求两条平行直线间的距离的最小值可以考虑以下不同路径：（1）求出两个点的坐标，求出两条平行线；（2）求出两个点的坐标，求出一条线；（3）求出两个点的坐标，不求线.

注意到x+y-3=0的斜率为-1，与斜率为1的直线互相垂直，A，B两点间的距离即要求的直线间的距离.数形结合，要充分发挥形的直观与数的精确两方面的优势，做“给出的题（数、形）”，而不是解一般的题.本题中数形结合思想、化归与转化思想运用作用十分明显.两个交点A（1，2），B（2，1），这时理科的第3题命题思路如出一辙，可见，命题人对数学思想方法的考查是刻意为之，是命题着重考虑的问题之一.

案例3（文科第12题）设函数f（x）=x3+3x2+1.已知a≠0，且f（x）-f（a）=（x-b）（x-a）2，x∈R，则实数a= _______，b=______.

解析：也许一些考生会被表面的三次方搞懵，没有完整地学习三次函数的性质啊！给出的是函数，有待求的未知数，不正是运用函数与方程思想的题材.

由f（x）-f（a）=x3+3x2+1-a3-3a2-1=（x-a）［x2+（a+3）x+ a2+3a］=（x-a）（x-a）（x-b），可知a，b应是方程x2+（a+3）x+ a2+3a=0的根，因此有x2+（a+3）a+a2+3a=0，解得a=-2或a=0（舍）.于是f（x）-f（a）=（x+2）2（x+1），可得a=-2，b=1.

当然，也可以直接考虑待定系数法：因为f（x）-f（a）= a3+3x2+1-a3-3a2-1=x3+3x2-a3-3a2，

且（x-b）（x-a）2=x3-（2a+b）x2+（a2+2ab）x-a2b，

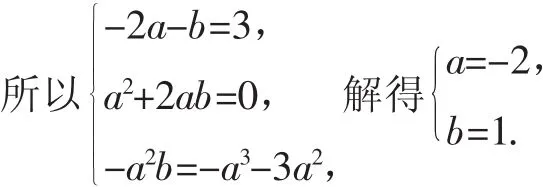
证明：（Ⅰ）f（x）≥1-x+x2；

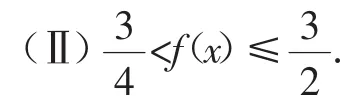
表面上涉及三次函数、分式函数，实际上，比较大小的根本大法是比差Ⅰ）迎刃而解；（Ⅱ）中，注意到（Ⅰ）f（x）≥1-x+x2，左边配方即可证明，右边不用任何技巧，直接作差，由x∈［0，1］得x4≤x3≤x≤1，2x4+x3-3x≤0，x3-1≤0，故，顺利求解，体现出考数学思想方法而不是考知识记忆、考数学素养而不是考模式套路的特点.数学背景的新颖才可以真实地检测应用数学知识、思想解决问题的水平，体现真正的数学素养的差异.

案例4（理科第18题）设a≥3，函数F（x）=min｛2|x-1|，x2-2ax+4a-2｝，其中

（Ⅰ）求使得等式F（x）=x2-2ax+4a-2成立的x的取值范围.

（Ⅱ）（i）求F（x）的最小值m（a）；

（ii）求F（x）在［0，6］上的最大值M（a）.

解析：记f（x）=2|x-1|，g（x）=x2-2ax+4a-2，根据题意为了确定f（x）、g（x）的关系，首先依托图形确定思路.注意到g（x）过定点（2，2），该定点又恰好在f（x）右支上，如图3，只要解出折线右支y= 2（x-1）与二次函数的右交点，方程2（x-1）=x2-2ax+4a-2，即x2-2（a+ 1）x+4a=0，一根已知，求解另一个根可以直接写出x=2a，故所求取值范围为［2，2a］；形的直观与数的准确（点（2，2）），数与形互帮互助，自然快捷.

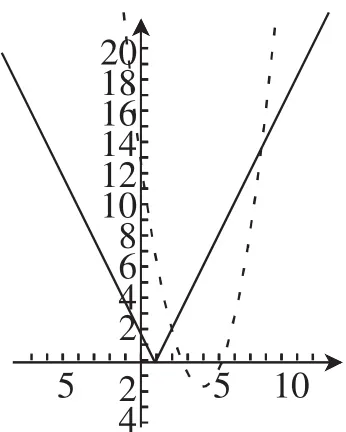
图3

（Ⅱ）（i）由于二次函数的对称轴x=a≥3，函数的最小值取决于min｛0，g（a）｝=min｛0，-a2+4a-2｝，下面就是简单的比较大小.

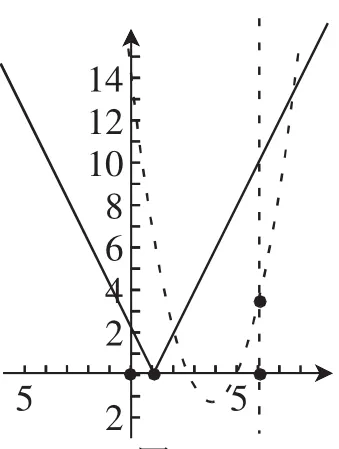
图4

（ii）求F（x）在［0，6］上的最大值M（a），根据图4可以看出，最大值的可能位置有三个，只要确定max｛f（0），f（2），g（6）｝=max｛2，34-8a｝，问题也就很简单.19题一题三问，含有参数，看起来挺复杂，实际上，只要思想清晰，数形结合，分类讨论，不断的转化问题，无论是解方程或者是不等式，计算量都很少.试题出发点重在数学思想方法.

三、核心素养的考查重在体现中学数学的六大核心素养的考查

即将颁布的《课程标准》中明确了中学数学的6个数学核心素养：数学抽象，逻辑推理，数学建模，数学运算，直观想象，数据分析.根据现行的课程标准下的高考，也可以看出以上核心素养的影子.核心素养的特点不同，考查侧重互异，限于篇幅，这里仅就数学运算这一大家比较关注的核心素养为例加以分析.

1.观察发现，多思少算

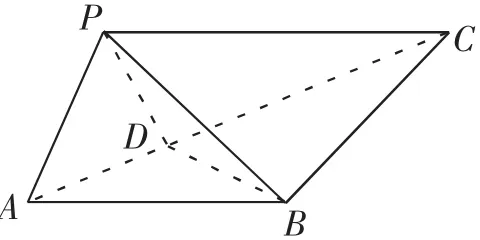
图5

案例5（理科第14题）如图5，在△ABC中，AB= BC=2，∠ABC=120°.若平面ABC外的点P和线段AC上的点D，满足PD=DA，PB=BA，则四面体PBCD的体积的最大值是_______.

解析：试题越来越注重考查学生的思维能力，计算不可或缺，但不再是烦琐量大的计算，更注重的是要求学生在短时间内开放思维，探索问题的本质.S△BCD的面积一边、一角已经确定，取决于CD，四面体的高取决于PD，猜想，点D位于AC的中点时所求体积最大，这时平面PBD⊥平面ABC.实际上，设PD=AC=x，h为三棱锥P-BCD的高，因为PB=PA，△PBD≌△ABD，当且仅当时，等号成立VP-BCD最大值为

解析：该题与案例5有异曲同工之妙.根据已知条件及双曲线的定义，|PF1|+|PF2|=2|PF2|+2，△F1PF2为锐角三角形，考虑两个极端位置：直角三角形△F1P1F2，△F1P2F2，两种情况下可以分别求出，进而得到所求的取值范围为

2.利用特值，多思少算

案例7（文科第6题）已知函数f（x）=x2+bx，则“b＜0”是“f（f（x））的最小值与f（x）的最小值相等”的（ ）

A.充分不必要条件 B.必要不充分条件

C.充分必要条件 D.既不充分也不必要条件

解析：本题充分条件的判断相对简单，必要条件的判断则需要一定灵活性，可以考虑比较特殊的情况，如b=0时，f（x）=x2，f（f（x））=x4，两个函数的最小值相等，不能推出b＜0，故选A.

案例8（理科第8题）已知实数a，b，c

A.若|a2+b+c|+|a+b2+c|≤1，则a2+b2+c2＜100

B.若|a2+b+c|+|a2+b-c|≤1，则a2+b2+c2＜100

C.若|a+b+c2|+|a+b-c2|≤1，则a2+b2+c2＜100

D.若|a2+b+c|+|a+b2-c|≤1，则a2+b2+c2＜100

解析：本题是大家一致反映比较难的一道题.教师的“难”主要是对背景的探索、一般方法的思考，学生主要难在形式不能进入计算.实际上，在考场上，只要取特殊值即可.如a=b=10，c=-110，排除A；a= 10，b=-100，c=0，排除B；a=100，b=-100，c=0，排除C.

另外，通过数形结合、设而不求等多种方法的应用，充分体现重点考查思维品质，减少计算量.

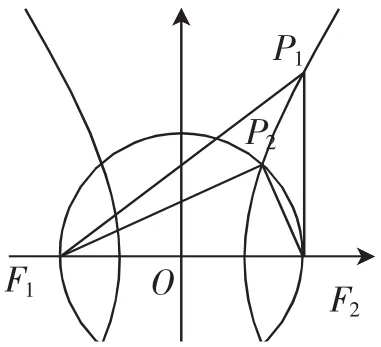
图6

由以上案例分析可以发现，数学离不开计算，素养下的数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题.主要包括：理解运算对象，掌握运算法则，探究运算方向，选择运算方法，设计运算程序，求得运算结果.重在运算法则的掌握、运算方向的探究、方法的选择，也就是“多一点想、少一点算”.

基于核心素养视角的教育教学将是今后相当长时间段内的热点，数学教学势必由知、能视角下的教学转变为有意识的核心素养的教学.关注核心素养下的数学教学是每一位数学教师义不容辞的责任.教学一线的教师不仅要明确核心素养的重要性，关键是弄清数学核心素养的内涵，探索数学知识教学与数学核心素养培育之间的途径，归纳、总结基于数学知识教学提升数学核心素养的方法和策略.

基于多次教改的经验，离开具体知识教学的支撑，核心素养的形成就会落空.知、能教学的成功经验、三维目标有效地落实举措不能偏废，还要继续发扬光大，数学核心素养的培养只能是“第三个包子”，前面两个“包子”“个大质优”才有“第三个包子”的完美效果.

1.柯跃海，陈清华.高考数学：命题目标的确立与实现［J］.数学通报，2013（1）.

2.何小亚.学生“数学素养”指标的理论分析［J］.数学教育学报，2015（1）.

3.陈昂，单旭峰，任子朝.我国高考命题的范式和范式转换研究［J］.中国高教研究，2015（3）.