POE策略在数学教学中的运用

☉江苏省东台中学 房 胜

POE策略在数学教学中的运用

☉江苏省东台中学 房 胜

数学是一门抽象程度较高的学科.高中数学中的很多概念已经愈来愈形式化，比如学生难以真正理解的函数概念、平面向量基本定理、圆锥曲线第二定义等一系列概念型的知识，也难以消化一系列抽象性的数学问题，典型的如抽象函数的定义域等.这些知识对于学生而言，形式化程度稍高，但是又有利于中学生思维的发展，因此抽象的数学问题一直是教学的重点和难点，如何将抽象数学教学演绎得更通俗易懂成为教师思考的一个问题.

根据心理学认知理论来说，抽象的知识要理解、认知，首先离不开其具体的问题载体，也就是具体情境，这个情境可以是生活中的，也可以是具体的、经过抽象的、但是存在具体形态的，只有具备这样的情境才能有助于学生对抽象知识有雏形上的认知，有助于其理解、思考、解决抽象问题.

一、POE策略界定

著名教育家皮亚杰提出过重要的概念同化理论，即其认为知识是经历“认知平衡—认知冲突—重新平衡”这样的阶段，即同化和顺应理论.1982年，波斯纳等研究者在此基础上提出了知识改变模式需要注重的几个条件：其一是原有具体形态知识不适用新的抽象学习范畴，必需有新的发展；其二是在原有基础提出的新的概念必需是可以理解的；其三是能解决现有问题并能形成体系.笔者认为，这些理论的发展其实说明了人类学习的过程，从感知学习—理性思考—抽象学习—形成体系.因此进一步的研究者创造了POE学习策略.

POE策略（Prediction-Observation-Explanation）是Gunstone和White正式提出的一种教学策略.其中文含义是“预测感知—观察思考—解释归纳”策略，这一策略偏重于学生的自我感知和理解，特别有助于抽象知识的学习，其通过学生的参与理解去感知抽象知识的形成过程，有助于抽象知识的理解和巩固.

二、POE策略下的抽象数学教学

数学概念教学是比较抽象和形式化的，尤其高中数学概念比初中数学概念的抽象性又向前大大迈进了一大步.很多高中数学概念对于学生而言，其抽象化程度比较高，非常不利于学生的理解.这些知识的传授，必须依赖具体的实际数学问题模型，进而思考问题的解决.

教学1：抽象函数定义域、函数性质的理解

1.函数定义域

定义域是函数三要素中最重要的一条，学生对于具备具体解析式的函数模型并不惧怕，但是对于抽象函数的定义域理解却相当薄弱.

案例1 函数y=f（x）的定义域为（1，2），求函数y= f（x+2）的定义域.

变式训练 函数f（x+1）的定义域为（-∞，1］∪［2，+∞），求函数f（x-1）的定义域.

POE教学策略：（1）预测感知：可以自己假定一个具体的函数模型出发，从模型研究中去思考函数定义域的求解，进而发展到抽象函数为载体进行理解；（2）观察思考：通过编制的具体函数模型求解到抽象的函数定义域求解的思考，发展抽象认知和思维；（3）解释归纳：将这一问题的解决进行反思，进而得到抽象函数定义域求解过程的理解，类似的方式处理不同的抽象函数其余问题.考虑到案例1学生大都能解决，因此笔者从POE教学策略的指导出发，主要以具体感知辅以抽象函数的方法通过类比解决变式训练：

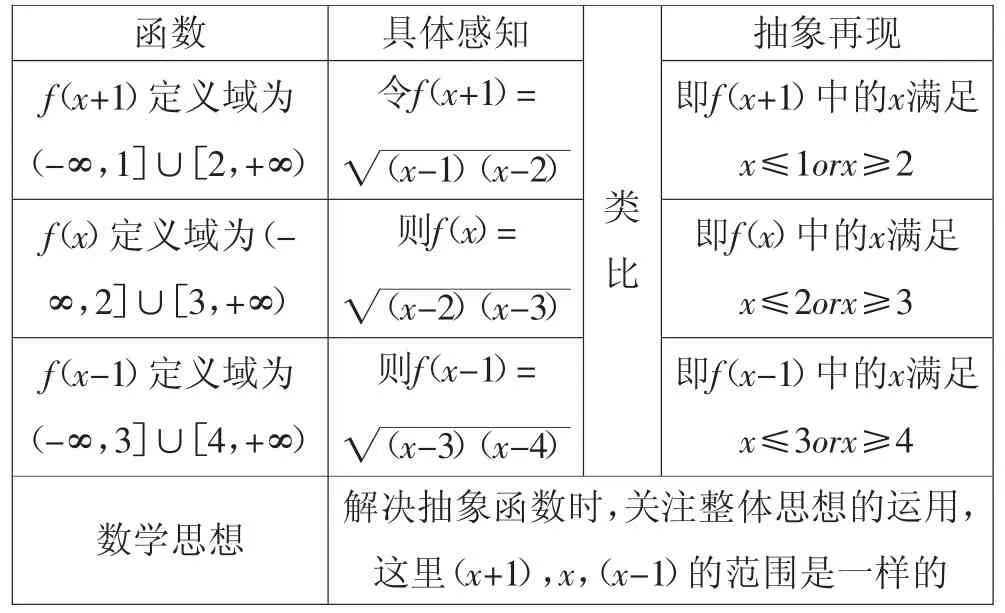
函数 具体感知类比抽象再现f（x+1）定义域为（-∞，1］∪［2，+∞）令f（x+1）=（x-1）（x-2）■即f（x+1）中的x满足x≤1orx≥2 f（x）定义域为（-∞，2］∪［3，+∞）则f（x）=（x-2）（x-3）■即f（x）中的x满足x≤2orx≥3 f（x-1）定义域为（-∞，3］∪［4，+∞）则f（x-1）=（x-3）（x-4）■即f（x-1）中的x满足x≤3orx≥4数学思想 解决抽象函数时，关注整体思想的运用，这里（x+1），x，（x-1）的范围是一样的

说明：通过具体编制的函数模型，学生能够解决任意类似的抽象函数定义域，其最终明白的要素是：第一，定义域永远指的是函数中的x的取值范围，而不是x+1、x-1等；第二，整体思想的介入，能让学生进一步理解对应法则f（*）中，*所代表的无论是x+1、x-1还是x，它们作为一个整体都是相同的范围.这两点的理解，是解决抽象函数定义域的关键.由此可见，POE策略从具体感知出发，结合抽象认知，最终归纳问题解决的结论，体现了其问题解决过程中步骤的合理性，也符合中学生心理认知结构和问题处理从特殊到一般的方式.

2.函数性质

函数有很多性质，其落实到抽象为载体的函数中，学生对性质就不能迅速的理解.教师教学中要使用合适的策略，使学生能从特殊的模型进而认知抽象的函数性质.我们知道，函数具备了轴对称性和中心对称性，以具体函数模型为例：f（x）=x2和g（x）=x显然具备了上述性质，将其转换为抽象表述，即f（-x）=f（x）以及g（-x）=-g（x），学生对这一具有具体解析式的函数模型结合抽象性质的理解还是比较到位的.将性质的认识提高到抽象程度，并一般化：

（1）函数y=f（x）满足f（a+x）=f（b-x），则函数y=f（x）的图像关于____________对称.

（2）函数y=f（x）满足f（a+x）+f（a-x）=2b，则函数y= f（x）的图像关于____________对称.

函数性质 具体感知类比抽象再现f（a+x）=f（b-x） 令f（x）=x2验证 直线x=a+b 2对称f（a+x）+f（a-x）=2b 令f（x）=x验证 点（a，b）对称

说明：通过函数具体模型，让学生进一步通过具体模型验证抽象表达式所表示性质的正确性，通过这一具体感知进而认知抽象结论.对学生而言，如何在没有具体模型的基础上以后理解这一抽象性质呢？笔者认为需要加强理解：以f（a+x）=f（b-x）为例，令x1=a+x，x2=b-x，则f（x1）=f（x2），对任意的x进行变换，我们可知自变量中点为不变量，而函数值（fx）=（fx），因此12随着x进行变换，显然（fx）永远有对称轴x）+f（a-x）=2b类似理解.从POE策略我们看出，对于问题的有效感知是前提，只有有有效的感知才能加强其抽象的理解，进而形成知识的巩固，这一策略在抽象数学教学中起着较大的作用.

三、POE策略下的具体数学教学

POE也能在具体形态的数学知识中实施，笔者以线性规划为例说明.

1.感知回顾

在学习了二元一次不等式（组）及其表示的区域……并且体会到在实际问题中的应用前景，感受到其重要性.首先一起回顾一下这些知识和方法：满足二元一次不等式组的x和y的取值构成有序数对（x，y），所有这样的有序数对（x，y）构成的集合称为二元一次不等式组的解集.回顾：其一，二元一次不等式Ax+By+C＞0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域；其二，二元一次不等式表示哪个平面区域的判断方法.

2.观察思考

思考：当z取不同值的时候，相对直线l0：2x+y=0而言，直线z=2x+y是向上平移了还是向下平移了？通过对z取特殊值，使学生对图像的变化有深刻的感受，从而得到随着z的值增大（或减小），直线l0会逐渐向上（或向下）平移；同样，当直线l0向上（或向下）平移时，z的值也会随着增大（或减小）.现在将上面的不等式组表示成平面上的区域，作直线l0：2x+y=0，然后作一组与直线l0平行的直线直线l：2x+y=t，t∈R.通过图像可以看出，直线l越往右移，t随之增大.从而得到zmax=2×5+2=12，zmin=2×1+1=3.

3.训练归纳

归纳：知识线：（1）线性规划的含义；（2）线性规划相关概念：目标函数、可行解、可行域、最优解等基本概念.思想方法线：（1）建模思想方法；（2）等价转化思想；（3）数形结合思想.

说明：本课是对于线性归纳基础概念的讲解，在一元二次不等式组基础上的加深，学生通过回顾—新知—归纳这一策略（POE具体形态知识中的运用），了解掌握图解法求解最优解.POE策略具体实施中，笔者并未详细讲述，而是以学案式学生探求为主的模式，学生在学习过程中得到了一定的自主精神和成功喜悦，也感受了代数问题图形化解决的数形结合思想的运用.通过POE策略充分调动学生的多种感官，达到教学要求，通过课堂练习大部分学生掌握了这一知识.

总之，POE策略正是通过预测暴露学生的前概念，通过感知认识使学生的认知发生冲突，通过辩解、讨论、类比最终实现学生的知识的转变.这符合学生的认知发展规律，与传统的教学策略相比在教学效果上具有明显的优越性.

1.任英杰.促进小学生“迷思概念”转变的POE策略及案例分析［J］.基础教育研究，2008（2）.

2.顾江鸿，等.预测—观察—解释——一种基于现代教育研究的演示策略［J］.教育科学研究，2009（5）.

3.赵国敏.化学概念转变教学中PEODE策略的探索和尝试［J］.化学教学，2014（4）.