高中数学课堂中“问题串”设计策略的思考

☉江苏省溧水高级中学 李宽珍

高中数学课堂中“问题串”设计策略的思考

☉江苏省溧水高级中学 李宽珍

《高中数学“问题串”教学模式的实践研究》是笔者主持研究的江苏省南京市教育科学“十二五”规划课题.该研究旨在改变高中数学传统教学的“一言堂”、“满堂灌”，从而教学效率不高等现象，为打造高中数学“优效课堂”提供一条有效途径，以期以较少的精力、有限的时间投入获得最优的教学效能.要真正地做到这一点，在数学教学中就要精心设计“问题串”.好的“问题串”能激发学生的学习兴趣，促进学生积极探究、思考，真正让数学课堂教学“活”起来，以达到事半功倍的教学效果.因此，在高中数学教学中开发“问题串”，并以之来组织教学，可以使得数学课堂高效.下面笔者结合平时的教学实践谈谈“问题串”的开发策略.

一、创设数学问题的情境中设计 “问题串”，激发学生的学习兴趣

学生在学习新内容前，课本新知识通常会与已有知识背景、与现实生活产生认知冲突，此时他们似懂非懂、似会不会，为了尽快消除认知失调带来的不悦，学生就会有迫切掌握知识的冲动和渴望.因此，在新课的导入中，根据学情和教学内容，在问题情境中精心设计“问题串”，使学生出现“愤徘”状态，从而充分调动起他们学习的兴趣与积极性，利于学生在获取知识的同时增长能力.

案例1“复数概念”教学，可以设计如下创设情境的“问题串”：

问题1 将10分成两部分，使两者的乘积为40.

问题2 有没有两个数之和为10呢？之积为40呢？

问题3 那为什么刚才的问题无解呢？（五百年前意大利数学家卡尔丹所遇到的问题）

问题4 实数集中有没有这两个数？

问题5 你知道数集的发展经历了几次扩充？

问题6 每一次扩充都解决了什么问题？

问题7 你能总结下几次数集扩充的共同特点吗？

问题8 你能写出卡尔丹要找的数吗？（引入什么样的数，才能解决负数不能开平方的矛盾呢？）

师：1545年，卡尔丹在《大衍术》中写道：“要把10分成两部分，使二者乘积为40，这是不可能的，不过我却用下列方式解决了：

师：1637年，法国数学家笛卡尔把这样的数叫做“虚数.1777年，瑞士数学家欧拉在其论文中首次用符号“i”规定：i2=-1，称i为虚数单位.新数i叫做虚数单位，并规定：（1）i2=-1；（2）实数可以与i进行四则运算，并且原有的加法与乘法的运算律仍然成立.

问题10 你还能写出其他含有i的数吗？

问题11 你能写出一个形式，把刚才所写出来的数都包含在内吗？

设计策略：这里设置的问题串，都是基于学生已有的知识经验与基础上提出，而且对相同的内容从不同的角度去思考，接地气，学生容易理解、接受.通过“问题串”的设置，学生形成了认知冲突；通过“问题串”的设置，引领了学生追溯历史，提炼数系扩充的原则；通过“问题串”的设置，帮助学生建立了新的认知结构，让数学理论自然诞生在学生的思想中.

二、数学概念的形成过程中设计 “问题串”，有助于学生对概念的理解

数学课程标准认为，概念的建构应该有四个重要环节：问题情境→学生活动→意义建构→数学理论.而根据维果茨基的理论，数学教学的高效就在于围绕学生“最近发展区”设计出科学的问题.由此，利用“问题串”进行数学课堂教学，这是符合新课改精神的，也应该成为我们数学教学的追求.

案例2“正切函数的图像及性质”教学，可以设计如下的“问题串”展示正切函数的图象及性质形成过程：

问题1 我们是怎样作出正弦函数的图像的？

问题2 你能简单说出作正弦函数图像的过程吗？

问题3 为何先作这个区间上的图像？

问题4 与正弦函数相比哪些地方需要修改？

问题5 你觉得作出正切函数的图像要分几步完成？

问题6 你能从正切函数图象出发，讨论它的性质吗？

设计策略：让学生理解并作出正切函数图像是本课的难点和重点，由于是学习了正余弦函数的图像与性质之后接触的另一个函数，故设计上述“问题串”，引导学生在不断的对比、类比中将已有的知识经验迁移到新内容中.同时，在解决问题的过程中，师生、生生讨论交流合作，自然地呈现数学概念的形成过程，进而实现教学目标.某种意义上说，“问题串”就是整节课的“骨架”，而问题就应该是设置在其最重要的“关节”处，具有较强的指向性、探究性、启发性和阶梯性.

三、探索数学的规律时设计“问题串”，提高探究能力

从数学的发展看，它本身也是充满着观察与猜想的探索活动.许多数学定理、性质、公式、法则的发现都经历了一个艰苦曲折的思维推理过程，教师应充分挖掘向学生展现“做数学”的过程.探索型问题串能较好地帮助教师引领学生参与此过程.探索型问题串的设计主要围绕定理、法则、和公式的发生、形成、发展三个过程展开，通过引导学生观察、动手操作、比较分析、猜想归纳，在“做数学”中学数学，获得数学学习的体验，提高探索能力，体味到数学的无穷魅力，以此促进学生的数学学习.

案例3“函数的零点存在定理”教学，可以设计引导学生探索数学规律的“问题串”：

如图，课前准备一根细绳（细绳两端记为A和B）、一支小棒.

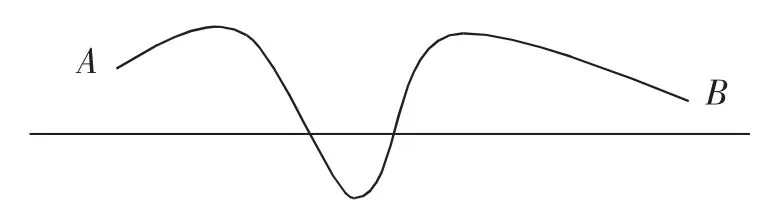
问题1 细绳和小棒何时有交点？

问题2 若将小棒视为轴，细绳视为函数的图像，能否将问题1中的结论用数学语言描述？

问题3 若细绳两端在棒的同侧（异侧），那么细绳和小棒的交点有几个？你发现有什么规律？能否用数学语言描述出来？

问题4 在什么样的条件下，细绳和小棒有且仅有一个交点？

问题5 根据刚才的实验操作，研究y=x4+2x3-2x2-2x的图象，并验证结论的正确性.

设计策略：本案例中五个问题由动手操作到进一步的追问，使学生从单纯的动手操作引向有意义的思考，再使之抽象到坐标系中，鼓励学生比较分析、大胆归纳，最后问题4的追问告诉学生要得到可靠的结论，需要逻辑的严格证明，培养学生严谨的治学态度，而问题5则是巩固和运用性质.五个问题以“为什么探究边性质→怎么探究→结论是什么→依据是什么→结论的推论是什么”为主线步步深入紧紧围绕性质的发生、形成、发展进行设计融合成一个整体.通过搭建“适切”的、脚手架式的5个问题串，一步一步、环环相扣、由浅入深，在“最近发展区”让学生处于“跳一跳”摘到了“桃子”的状态，达到“道而弗牵，强而弗抑，开面费达”的境界.

四、探究解决问题的方法时设计 “问题串”，拓宽学生的思路

问题串教学让数学课堂教学走向自主、合作与开放.通过问题变式，提出恰当的，对学生数学思维有适度启发的问题，可引导学生思考和开展探究活动；同时它能激发学生最大限度地来体验与参与发现、设计创新，形成一种积极、主动、探究的高效学习方式，在这个学习过程中会产生许多有价值的生成性资源，有利于学生探究能力和创新精神的培养，提高解决问题的能力.

案例4“求数列的通项公式”教学，设计求解数列通项公式的问题串：

基于学生学习了等差、等比数列的通项公式以后，专门探究求数列的通项公式的题型与方法.

例题 已知数列｛an｝的前n项和Sn=n2+1，求通项an.

问题1 已知数列｛an｝的前n项和为Sn，若log2（Sn+1）= n+1，求an.

问题2 已知数列｛an｝中，若2n+5，求an.

问题3 已知数列｛an｝中，a1=1，n≥2时，有a1·a2·…· an=n2，求a3+a5.

问题4 已知数列｛an｝中，a1=1，an+1-an=2n，求an.

问题5 已知数列｛an｝中，a1=2，Sn=n2an，求an.

问题6 已知数列｛an｝中，a1=1，n≥2时，an=3an-1+2，求an.

设计策略：本课例的问题串设计，以最基础的例题为出发点，通过改变已知条件，设置不同情境下的问题串，从而引出了求数列通项公式的六种常规方法，让学生在在实际操作中获取知识，同时培养了学生的比较、分析、综合、归纳等能力，养成归纳反思的好习惯.变式型“问题串”主要以教科书中例、习题为对象，在保持原题本质的基础上进行延伸拓展，通常变换条件或结论或因果关系倒置.通过变式型问题串的训练，学生对某一孤立、零散的问题形成有规律可循的一系列问题，对所学知识举一反三、触类旁通，从而提高课堂教学的有效性.

五、纠错过程中设计“问题串”，增加学生对错题的“免疫力”

学生在数学学习中出现错误是不可避免的，它往往能暴露学生的真实想法，反映学生的思维过程，包含着有价值的成分.教师若能善于发现错误背后隐藏的价值，巧用典型错误，通过设计“问题串”，变换问题的条件和结论，变换问题的形式，而不变换问题的本质，使学生更容易看清问题的本质.

案例5 针对学生作业中的错题：“已知a∈R，若任意的x∈（0，+∞），都有［（a-1）x-1］（x2-ax-1）≥0，则实数a的取值集合是______.”设计以下问题串以求解决这类问题的通法：

学生在解决这个问题时出现错误，在给学生解决方法后可以设计一下问题串，帮助学生进一步的理解.

问题1 已知（2ax-1）lnx≥0对任意x∈（0，+∞）恒成立，则实数a的取值集合是________.

问题2 已知t＞0，若任意的x∈（0，+∞），不等式txlnx+20lnt≥txlnt+20lnx恒成立，则实数t的取值集合是_________.

问题3 已知t＞0，若任意的n∈N*，不等式ntlnn+ 20lnt≥ntlnt+20lnn恒成立，则实数t的取值集合是_________.

通过对4个问题的练习与讲解，使学生对这类题的本质的了解更加全面，在应对高考过程中真正地做到了未雨绸缪.波利亚说：当你找到第一个蘑菇或做出第一个发现后，再四处看看，它们总是成群生长的，问题串就是那成群生长的蘑菇.设计“问题串”的目的是帮助学生在跳出题海的同时对所学的知识能够融会贯通，从而达到学习的优效、高效，体会学习数学的乐趣.

好的问题是一堂成功的数学课的重要组成部分，成功的问题串设计可以打开学生学生的思维，培养学生的创新能力.作为一线教师，我们要经常反思我们的数学教学，精心设计好数学教学的“问题串”，不断追求问题串的精湛、精准，让学生在获取知识的同时增长能力，真正提高课堂教学效率与质量.